ЛЕКЦИЯ 6 Поверхности

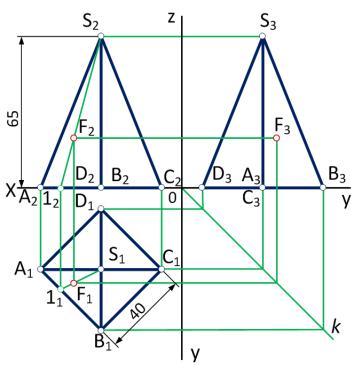
Для изображения поверхности на чертеже необходимо вычертить очерки поверхности и указать видимость поверхности по отношению к плоскостям проекций. Для определения видимости поверхности относительно плоскостей проекций используют конкурирующие точки или рассматривают взаимное расположение частей поверхности.

Точка на поверхности. Точка принадлежит поверхности, если она лежит на линии, принадлежащей данной поверхности. Задачи на принадлежность точки поверхности с использованием простейших для построений линий - образующих или параллелей, принадлежащих поверхности.

Примеры.

1. Эпюр четырехгранной пирамиды (рис. 78)

Известно: в основании пирамиды находится квадрат с длиной стороны 40мм, высота пирамиды 65 мм. Основание пирамиды принадлежит горизонтальной плоскости проекций.

1. Строим горизонтальную проекцию пирамиды - квадрат A1B1C1D1 со стороной

40 мм.

Основание пирамиды

АВСDϵ 1, поэтому проецируется на эту плоскость в натуральную величину. Горизонтальная проекция вершины пирамиды S1 лежит на пересечении диагоналей квадрата. Соединяем вершину S1 с проекциями точек основания – получаем проекции ребер пирамиды.

2. Выполняет фронтальную проекцию пирамиды. Фронтальная проекция основания A2B2C2D2 лежит на

оси х, т.к. АВСDϵ 1.

Затем строим вершину S пирамиды, учитывая, что высота пирамиды равна 65мм. Соединив проекции вершины пирамиды с проекциями вершин основания, получим проекции боковых ребер.

3. Строим профильную проекцию пирамиды, используя постоянную чертежа прямую k. Если нужно на проекциях пирамиды построить точку, например, точку F, лежащую на одной из его граней, то следует на эпюре «связать» точку с соответствующей гранью при помощи какой-либо прямой.

2 Эпюр прямого кругового конуса (рис. 79)

Известно: диаметр окружности основания 40мм, высота пирамиды 60 мм. Основание пирамиды принадлежит горизонтальной плоскости

1.Вычерчиваем горизонтальный очерк прямого кругового конуса – окружность диаметром 40 мм. Горизонтальная проекция

вершины S1 совпадает с проекцией центра окружности основания.

2.Строим фронтальный очерк - треугольник высотой 60 мм и основанием 40 мм.

3.Построение профильного очерка выполняем, используя постоянную чертежа - прямую к.

В таблице 1 приведены чертежи некоторых геометрических тел и показано построение проекций точки, принадлежащих поверхности геометрического тела.

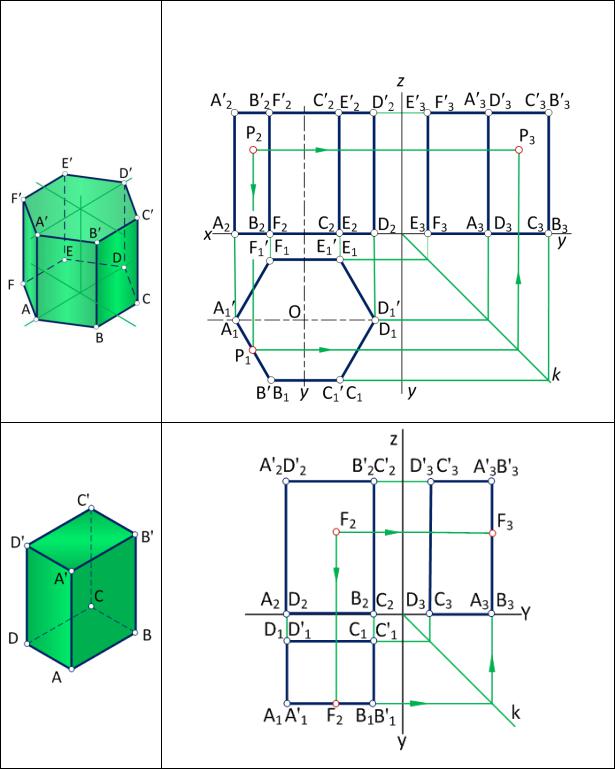
Таблица 1

Прямоугольный

параллелепипед