Функции нескольких переменных

На практике часто встречаемся с величинами, значения которых зависят от нескольких величин, изменяющихся независимо друг от друга. Рассмотрим простейший случай, когда таких независимых переменных две.

Пусть М – некоторое множество пар действительных чисел. Функцией двух переменных называется правило (закон), по которому каждой паре чисел ставится в соответствие единственное число, при условии, что каждоесоответствует хотя бы одной паре.

x,y – независимые переменные;

М – область определения;

Z – область значений;

Так как каждой паре соответствует единственная точкаP(x, y) и обратно, то функцию двух переменных можно рассматривать как функцию точки Р.

Если функция двух переменных задана с помощью аналитического выражения (формулы) без каких-либо дополнительных условий относительно области определения, то областью определения принято считать множество таких точек плоскости Оxy (пар ), для которых это аналитическое выражение имеет смысл и дает действительное значение функции.

Пример: функция определена для всех точекплоскости Оxy, кроме точек прямой x-y=0.

Частные производные

Рассмотрим функцию двух переменных . Зафиксируем одну из переменных, например, пусть. Тогда-- функция одной переменнойх.

-- частное приращение функции по переменнойх.

Аналогично, если зафиксируем х=х₀, то

-- частное приращение функции по переменнойy.

Если существуют конечные пределы, то:

--

называется частной производной по х (или частной производной первого порядка);

--

называется частной производной по y.

Выводы:

1. Частная производная функции двух переменных по одному из ее аргументов равна пределу отношения частного приращения функции к вызвавшему это приращение аргументу, когда приращение аргумента стремится к нулю.

2. Частные производные в точке (x_0, y₀) – это числа, зависящие от координат точки, в которой вычисляются, то есть в общем случае это функция двух переменных.

3. Частная производная определяется как производная функции одной переменной (другую переменную фиксировали), поэтому для частных производных справедливы все правила и формулы дифференцирования функции одной переменной. Следует помнить, что при нахождении частной производной какому-либо аргументу, все аргументы считаются постоянными.

Примеры

1) ;

.

2) ;

.

Частные производные высших порядков

Частные производные первого порядка есть функции двух переменных и, в свою очередь, могут иметь частные производные.

Если существуют частные производные от частных производных по x и y, то их называют частными производными второго порядка и обозначают:

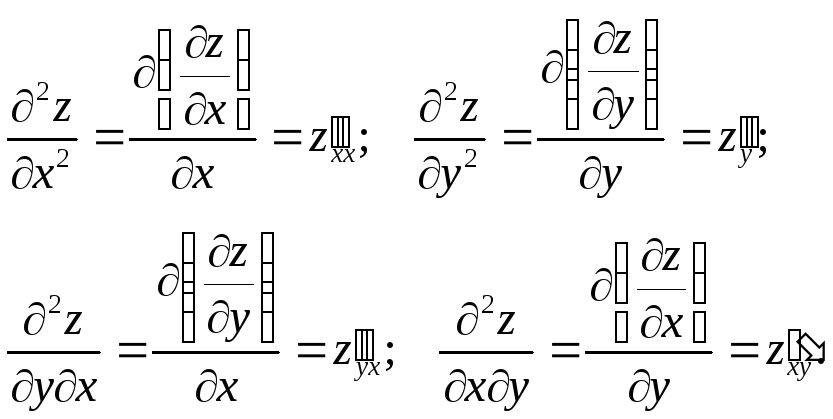
Частные производные, вычисленные по различным аргументам, называются смешанными.

Теорема. Если смешанные производные есть непрерывные функции, то они равны между собой:

.

Аналогично определяются производные третьего и более порядков.

Производная по направлению. Градиент

Скалярным полем называется часть пространства (или все пространство), каждой точке которой соответствует численное значение некоторой скалярной величины.

Примеры

Тело, имеющее в каждой точке определенное значение температуры – скалярное поле.

Неоднородное тело, каждой точке которой соответствует определенная плотность – скалярное поле плотности.

Во всех этих случаях скалярная величина U не зависит от времени, а зависит от положения (координат) точки М в пространстве, то есть -- это функция трех переменных, она называетсяфункцией поля. И обратно, всякая функция трех переменных u=f(x, y, z) задает некоторое скалярное поле.

Функция плоского скалярного поля зависит от двух переменных z=f(x, y).

Рассмотрим скалярное поле u=f(x, y, z).

Вектор, координатами которого являются частные производные функции, вычисленные в заданной точке, называется градиентом функции в этой точке.

или

Рассмотрим некоторый вектор и на нем две точкиM₀(x₀, y₀, z₀) и . Найдем приращение функции в направлении:

.

Производной по направлению называется следующий предел, если он существует:

.

где -- направляющие косинусы вектора; α, β, γ -- углы, которые образует вектор с осями координат.

Для функции двух переменных эти формулы принимают вид:

или ,

т

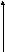ак как.

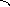
Между градиентом и производной по направлению в одной и той же точке существует связь.

Теорема. Скалярное произведение градиента функции на вектор некоторого направления равно производной данной функции в направлении этого вектора:

.

Следствие. Производная по направлению имеет наибольшее значение, если это направление совпадает с направлением градиента (обосновать самостоятельно, используя определение скалярного произведения и считая, что ).

Выводы:

1. Градиент – это вектор, показывающий направление наибольшего возрастания функции в данной точке и имеющий модуль, численно равный скорости этого возрастания:

.

2. Производная по направлению – это скорость изменения функции в направлении : если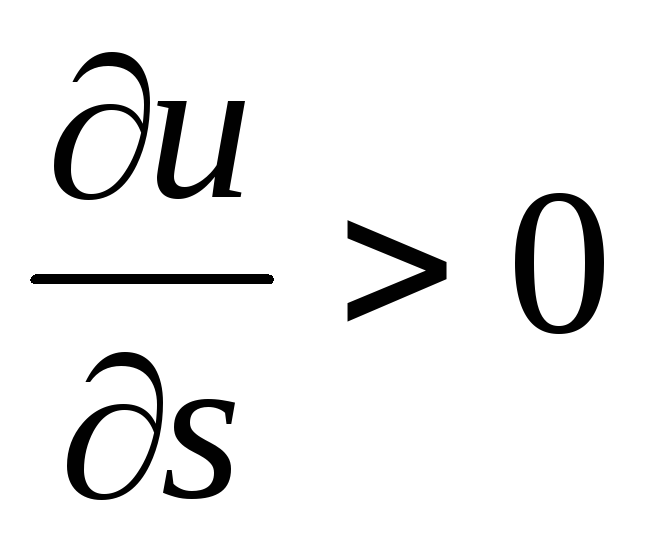, то функция в этом направлении возрастает,

если , то функция убывает.

3. Если вектор совпадает с одним из векторов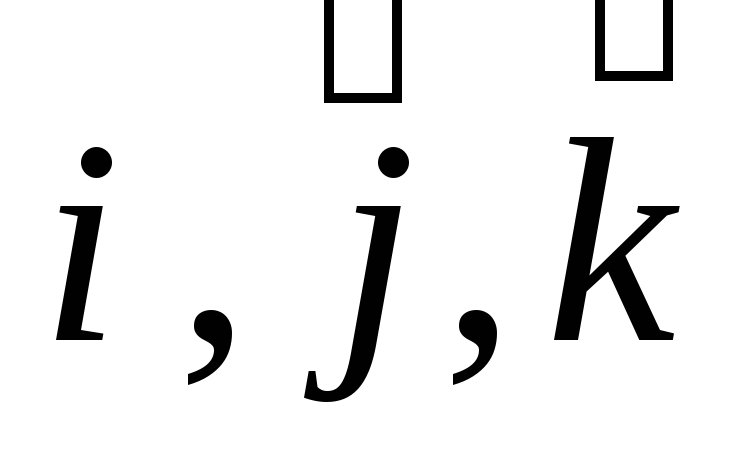, то производная по направлению этого вектора совпадает с соответствующей частной производной.

Например, если , тогда.

Пример (см. задание VII)

Даны функция , точкаА(1, 2) и вектор .

Найти: 1) ;

2) .

Решение.

1. найдем частные производные функции и вычислим их в точке А.

, .

Тогда .

2. Найдем направляющие косинусы вектора :

.

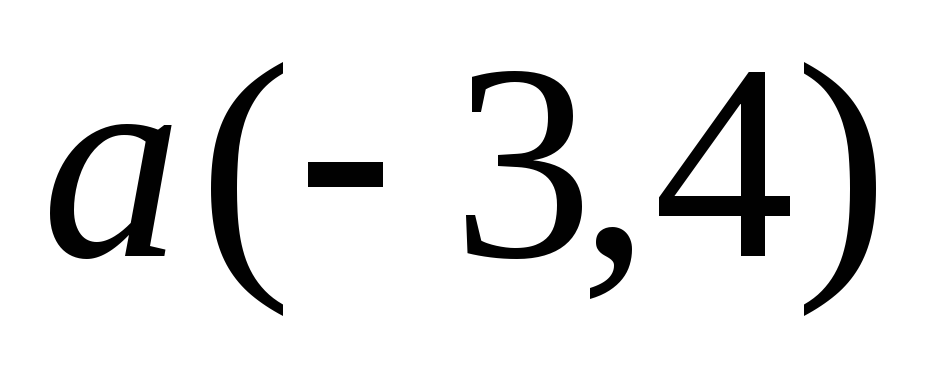Тогда .

Ответ: ;

.

Ниже приведены задания для контрольной работы.

Номер варианта соответствует последней цифре Вашего шифра. Из каждого задания необходимо выполнить пример, номер которого совпадает с номером Вашего варианта.

Каждую контрольную работу следует выполнять в отдельной тетради. Следует указать свой шифр и номер варианта. Условие задачи должно быть полностью переписано перед ее решением.

Отмеченные рецензентом ошибки необходимо исправить в конце работы, сделав работу над ошибками.

Зачтенные контрольные работы предъявляются студентом при сдаче зачета или экзамена.