14.10. Схема замещения фазы асинхронного двигателя

Для расчетов рабочих процессов асинхронного двигателя часто используется схема замещения фазы двигателя, состоящая из резистивных и индуктивных элементов с постоянными параметрами, а также резистивного элемента с переменным сопротивлением, замещаю­щим механическую нагрузку на валу двигателя.

Для обоснования такой схемы замещения преобразуем соответст­вующим образом основные уравнения состояния двигателя. Для этого все роторные величины приведем к числу витков, обмоточному коэффи­циенту и числу фаз статора подобно тому, как мы приводили к числу витков первичной обмотки трансформатора величины, относящиеся ко вторичной обмотке (см. § 8.5). Асинхронный двигатель является трех­фазным устройством, но его фазы симметричны, поэтому достаточно составить схему замещения для одной фазы.

Электродвижущая сила фазы статора Е₁ связана с ЭДС фазы не­подвижного эквивалентного ротора Е_2н соотношением

Е₁ = (w₁k_o61/w₂k_o62) Е_{г н} = k_eE_{2 H},

где k_e — коэффициент трансформации напряже­ний асинхронной машины.

Согласно векторной диаграмме фазы двигателя (рис. 14.18)

—_2н =(+jL_рас2) ₂ = (r_В2 + r₂ +jL_pac2) ₂ = Z_o622 + г₂₂.

Следовательно,

—₁ = (Z_o62 + r₂)k_e2.

Ток фазы ротора ₂ можно заменить приведенным током:

₂= (Зw₁k_об1/m₂w₂k_об2) ’₂ = k_i’₂

где k_i — коэффициент трансформации токов асинхронной машины. Сделав подстановку, получим:

₁ = — (Z_{o6 2} + r₂) k_ek_i’₂.

Произведение k_ek_i = k есть коэффициент трансформации асинх­ронной машины.

Введем теперь в уравнения электрического состояния фазы статора асинхронного двигателя приведенные сопротивления цепи ротора:

k_ek_i Z_об2 = Z’_0б2 И k_ek_i r₂ = r’₂.

Элементы с такими сопротивлениями в цепи фазы статора будут потреблять такую же энергию и при том же сдвиге фаз между током и напряжением, как это имеет место в соответствующих сопротивле­ниях элементов цепи фазы ротора по схеме на рис. 14.17.

Таким образом, ЭДС фазы статора равна:

₁ = - (Z’_об2 + r’₂) ’₂

а напряжение статора (фазное)

₁ = (-₁ ) + Z_o611 = Z_o611 + (Z_o62 + r’₂) ’₂. (14.18)

С другой стороны, ЭДС₁ пропорциональна намагничивающему току _1x и по тем же соображениям, как и для трансформатора, напряжение

(—₁) = Z_121x,

где условная величина Z₁₂, модуль которой имеет размерность сопро­тивления, в эквивалентной схеме замещения соответствует магнитной цепи двигателя. Следовательно, для напряжения фазы статора спра­ведливо также второе уравнение

₁ = Z_{0б1 1} + Z_{12 1х}. (14.19)

Вместе с уравнением тока статора

₁ =_1х +’₂ (14.20)

два уравнения напряжения фазы статора (14.18) и (14.19) можно рас­сматривать как уравнения, соответствующие законам Кирхгофа для цепи на рис. 14.19. В ней элементы Z_o61 изображают схему замещения обмотки фазы статора, Z’_qб2 — обмотки фазы ротора, Z₁₂ — магнитную цепь машины, a r'₂ — механическую нагрузку.

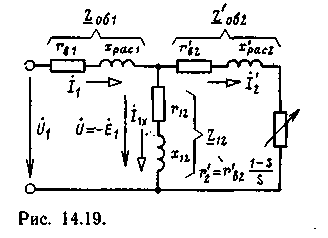
Уточним, что ток _1х является то­ком фазы статора идеального холосто­го хода двигателя, т. е. это ток двига­теля в условиях, когда ток в роторе отсутствует (I₂ = 0). Ток 1_1x можно измерить, если посредством внешнего двигателя довести ротор до синхрон­ной частоты вращения (s = 0).

При такой синхронной частоте вращения сопротивление резистив­ного элемента, соответствующего механической нагрузке в эквива­лентной схеме замещения, равно (14.16):

r'₂ = r'_B2/s — r'_B2 = r'_B2 (1 — s)/s =.

Если затормозить двигатель до полной остановки, то s = 1 и, сле­довательно,

r'₂= 0.

По этой причине опыт полной остановки двигателя именуется опытом короткого замыкания — обычно он осуществляется при сильно пониженном напряжении на статоре.