14.12. Вращающий момент асинхронного двигателя

Выражение для вращающего момента асинхронного двигателя можно получить из формулы для механической мощности Р_мех на валу двигателя:

М_вр=Р_мех/_р, (14.22)

где _р — угловая скорость ротора.

Так как угловая скорость ротора _р = 2n/60, то, следовательно, связь между угловыми скоростями магнитного поля _п двигателя и ротора _р определяется скольжением

S = (n₁ - n)/п₁ =( _п -_р )/ _п,

или

_p = _п (l-s).

Угловая скорость вращающегося магнитного поля _п равна угло­вой частоте синусоидального тока в фазных обмотках статора со для двухполюсного двигателя (р = 1). В общем случае многополюсного двигателя угловая скорость магнитного поля равна:

_п= /p,

где р — число пар полюсов.

Подставив в (14.22) выражение _p через , получим:

Мвр =Pмех. (14.23)

Из анализа схемы замещения фазы двигателя (рис. 14.19) известно, что механическая мощность на валу равна:

Pмех = 3r’₂(I’₂)²=3r’_B2(I’₂)²=r_B2m₂I²₂ (14.24)

Подставив значение механической мощности на валу двигателя из (14.24) в (14.23), получим выражение вращающего момента:

М_вр =m₂pr_B2I²₂/s, (14.25)

а так как r_B2I₂ = E₂ cos ф₂ на основании векторной диаграммы фазы ротора (рис. 14.15), a E/s = E_2H, то, следовательно,

М_вр = E_2нI₂соsф₂. (14.26)

Чтобы ввести в выражение момента на валу (14.26) значение маг­нитного потока вращающегося поля, заменим согласно (14.12)

E_2н= 4,44fw₂6k_о62Ф_в = w₂ k_об2Ф_в/ и получим:

М_вр = m₂рw₂k_об2Ф_вI₂ cos ф₂ = const Ф_вI₂ cos ф₂, (14.27)

т. е. вращающий момент двигателя пропорционален произведению по­тока вращающегося магнитного поля и тока в обмотке ротора.

14.13. Механическая характеристика асинхронного двигателя

Для устойчивой работы двигателя важно, чтобы автоматически устанавливалось равновесие вращающего и тормозного моментов; с увеличением нагрузки на валу двигателя должен соответственно возрастать и вращающий момент. Это уравновешивание у работаю­щего асинхронного двигателя осуществляется следующим образом: при увеличении нагрузки на валу тормозной момент оказывается больше вращающего момента, вследствие чего частота вращения ро­тора уменьшается — скольжение возрастает. Повышение скольжения вызывает увеличение вращающего момента, и равновесие моментов восстанавливается при возросшем скольжении.

Однако зависимость вращающего момента от скольжения довольно сложна.

Действительно, в уравнении вращающего момента (14.27) все три величины I₂, Ф_в и cos ф зависят от скольжения.

Ток ротора I₂ (см. § 14.7) с возрастанием скольжения быстро уве­личивается вследствие увеличения ЭДС E₂, пропорциональной сколь­жению. Сначала, пока индуктивное сопротивление рассеяния обмотки ротора sL_pac2 мало по сравнению с ее активным сопротивлением r_в2, значение тока при увеличении скольжения возрастает быстро, а затем, когда sL_pac2 = r_в2, все медленнее.

Коэффициент мощности цепи ротора

cos ф₂ = r_s2/

вследствие возрастания скольжения уменьшается сначала медленно, а потом все быстрее. Полезно пояснить физические условия, опреде­ляющие влияние cos ф₂ на вращающий момент.

Для этого достаточно обратиться к крайним идеальным условиям — предположить, что cos ф₂ = 0, т. е. принять, что обмотка ротора обладает только индуктивным сопротивлением. В таких условиях токи в обмотке ротора будут иметь наибольшее значение в тех проводниках ротора, в ме­сте расположения которых индукция была максимальной четверть периода тому назад (рис. 14.21). Ток будет иметь максималь­ное значение там, где индукция вращаю­щегося магнитного поля отсутствует, а си­лы, действующие на остальные провода ро­тора, будут взаимно уравновешиваться и вращающий момент на валу двигателя бу­дет равен нулю.

В реальных условиях асинхронного двигателя цепь ротора обладает как ак­тивным, так и индуктивным сопротивлением, причем последнее из­меняется пропорционально скольжению, что соответственно сказы­вается на вращающем моменте машины.

Влияние скольжения сказывается и на главном потоке машины Ф_B хотя и в меньшей мере. С увеличением скольжения возрастает ток I; статора, а следовательно, уменьшается ЭДС

₁ = ₁ — Z_o61I₁

и пропорциональный ей магнитный поток Ф_в, так как (14.10)

Ф_в = E₁/4,44fk_о61.

В выражении момента (14.27) три величины зависят от скольже­ния, причем одна из них I₂ увеличивается с ростом скольжения, а две другие — Ф_в и cos ф₂ убывают. Следовательно, определенному значению скольжения, называемому критическим скольжением s_kp, должно соответствовать максимальное значение вращающего момента. Чтобы определить условия максимума момента на валу через пара­метры машины, обратимся к выражению момента (14.25), в котором I₂ определим из схемы замещения фазы статора (рис. 14.19) без учета тока холостого хода I_1х:

Mвр=(14.28)

Возьмем первую производную от выражения вращающего мо­мента (14.28) по скольжению и приравняем ее нулю:

(14.29)

= Ur^’_B2

Нулю может быть равен только числитель этого выражения, следо­вательно, критическое скольжение, соответствующее максимуму момента, будет:

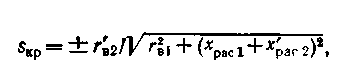
здесь знак минус относится к работе машины в режиме генератора. Так как у машин значение r²_в1 составляет не более 5 % значения под­коренного выражения, то можно этой величиной пренебречь и считать, что критическое скольжение, выраженное через приведенные пара­метры цепи ротора, будет:

s_Kp = ±r'_B2/(x_pac,₁ + x'_pac2). (14.30)

Если заменим r'_B2= kr_B2; x'_pac2 = kx_pacc2; x_pacl/k = x”_pacl, то получим выражение s_Kp через роторные сопротивления r_в2, x_рас2 и x_pacl - индуктивное сопротивление рассеяния фазной обмотки статора, приве­денное к числу фаз, витков и обмоточному коэффициенту ротора:

s_Kp = ±r_B2/(x”_pacl+x_pac2). (14.31)

Индуктивность рассеяния обмоток ротора относительно велика, так как проводники лежат в пазах сердечника; поэтому максимальный момент двигателя обычно соответствует весьма небольшим скольже­ниям, а именно 4 % у двигателей большой мощности и до 14 % у дви­гателей малой мощности.

Характерный график зависимости вращающего момент двигателя от скольжения показан на рис. 14.22. Максимум вращающего момента разделяет график вращающего момента на устойчивую часть от s = 0 до s_Kp и неустойчивую часть — от s_Kp до s = 1, в пределах которой вращающий момент уменьшается с ростом скольжения.

У работающего двигателя динамиче­ское равновесие моментов автоматически восстанавливается при увеличении ско­льжения, пока тормозной момент на ва­лу меньше максимального момента дви­гателя. Но когда тормозной момент до­стиг значения максимального момента двигателя, тогда при дальнейшем увели­чении нагрузки возрастание скольжения будет лишь уменьшать вра­щающий момент: таким образом, динамическое равновесие, нарушен­ное увеличением нагрузки, не восстанавливается и вследствие преоб­ладания тормозного момента двигатель останавливается.

Выразим теперь максимальный вращающий момент через параметры машины; для этого подставим выражение критического скольжения (14.30) в уравнение момента (14.28).

Пренебрегая значением величины л_в1 по сравнению со значением величины (х_рас1 + х'_расг), получим выражение максимального момента асинхронного двигателя в следующей простой форме:

(14.32)

M_max=.

Максимальный момент определяет перегрузочную способность асинхронного двигателя. Выражение (14.32) показывает, что М_тах не зависит от активного сопротивления цепи ротора, в то же время согласно (14.30) и (14.31) критическое скольжение пропорционально этому сопротивлению. Следовательно, можно, увеличивая активное сопротивление цепи ротора, увеличивать критическое скольжение, не изменяя максимальный момент. Это используется для улучшения пусковых условий в двигателях с фазным ротором.

То обстоятельство, что максимальный вращающий момент пропор­ционален U²₁, делает асинхронный двигатель весьма чувствительным к снижению напряжения питающей его сети. При значительном сни­жении U₁ вращение двигателя при пуске в ход может не начаться.

У нормальных асинхронных двигателей максимальный момент больше номинального в 2—2,5 раза.

Для целей электропривода большое зна­чение имеет зависимость частоты вращения двигателя от нагрузки на валу п (М); эта зависимость носит название механической ха­рактеристики. По своей форме она отличает­ся от кривой М_вр (s) только положением по отношению к координатным осям.

Как показывает кривая рис. 14.23, частота вращения асинхронного двигателя лишь не­значительно снижается при увеличении вращающего момента в пре­делах от нуля до максимального значения, т. е. механическая ха­рактеристика двигателя в этом случае жесткая.

При перегрузке свыше максимального момента М_тах (что состав­ляет примерно двух-, трехкратную перегрузку) двигатель входит в об­ласть неустойчивого режима (если тормозной момент на валу постоя­нен) и останавливается. Это обстоятельство вынуждает выбирать мощ­ность двигателя так, чтобы даже при кратковременной перегрузке не был превышен максимальный момент; в противном случае привод дол­жен быть снабжен соответствующим маховиком.

Механическая характеристика, относящаяся к нормальным рабо­чим условиям машины, называется естественной механической харак­теристикой в отличие от искусственной механической характери­стики, какой является, например, характеристика двигателя с фазным ротором, когда в цепь ротора включен реостат.