48. Постановка и классификация детерминированных задач оптимизации.

Под решением задачи понимают процесс выбора управляемых переменных , принадлежащих допустимой области и обеспечивающих оптимальное значение некоторой характеристики объекта .

Задача называется задачей оптимизации с ограничениями или задачей условной оптимизации. Задача, в которой нет ограничений, т.е.

; называется задачей безусловной оптимизации.

Задачи, в которых представляет собой одномерный вектор , называются задачами одномерной оптимизации. Если число варьируемых переменных больше единицы , то такие задачи являются задачами многомерной оптимизации, связанными с оптимизацией некоторой n-мерной гиперповерхности

Задачи условной оптимизации, в которых функции и являются линейными, носят название задач с линейными ограничениями. В таких задачах целевые функции могут быть либо линейными, либо нелинейными. Задачи с линейной целевой функцией и линейными ограничениями и являются задачами линейного программирования (ЗЛП).

Если целевая функция - квадратичная функция, а ограничения и - линейные функции, то задача (1)-(4) является задачей квадратичного программирования. В тех случаях, когда критерий оптимальности или ограничения и представляют собой нелинейные функции переменных , задача (1)-(4) является задачей нелинейного программирования.

49. Многокритериальные задачи оптимизации.

В практике часто возникает необходимость найти решение, которое бы являлось наилучшим с позиций нескольких различных критериев .

Решение задачи многокритериальной оптимизации (компромиссное решение) () является эффективным решением, если для него справедливо неравенство

,

Первый подход — выбор основного критерия. Один из путей учёта совокупности противоречивых критериев состоит в том, что какой либо из критериев выбирается в качестве основного, а остальные критерии считаются вспомогательными. Оптимизацию осуществляют по основному (одному) критерию, а на все остальные критерии накладывают ограничения.

Второй подход — ранжирование критериев. Пусть критерии ранжированы и номер критерия обозначает номер ранга. Очевидно, что оптимизацию следует начинать с критерия первого ранга

(18)

Третий подход — формирование обобщённого критерия. Идея этого метода проста: построить обобщённый скалярный критерий

(24)

как функцию исходных критериев. Пусть минимизируются все частные критерии, чего легко добиться, умножив максимизируемые критерии на -1. При этом минимум обобщённого критерия (24) должен соответствовать решению многокритериальной задачи. Тогда решение поставленной задачи сведётся к обычной оптимизации

. (25)



50. Одномерная оптимизация.

4.1. Метод равномерного поиска

Пусть априорная информация об унимодальности функции крайне недостаточна, чтобы строить разумный процесс поиска экстремума. Наиболее приемлемым способом поведения в такой обстановке является последовательное вычисление целевой функции I(y) при всех допустимых значениях варьируемого параметра y

a  y  b ,

где a, b - границы интервалов поиска.

Пусть  заданная величина погрешность определения оптимального параметра y*. Тогда для реализации алгоритма поиска следует определить значение I(y) в

точках, равномерно отстоящих друг от друга на расстоянии h=, т. е. в точках

Из полученных значений показателя качества I(y_j) выбирается наибольшее значение (глобальный максимум). Такой способ поиска называется сканированием. При малой заданной погрешности  этот метод требует слишком большое число вычислений функции I(y) и больших затрат машинного времени.

4.2. Метод поразрядного приближения

Этот метод применим для поиска оптимума унимодальной функции и обладает более высоким быстродействием. Это достигается тем, что используется алгоритм с переменным шагом поиска. Вначале величина шага выбирается достаточно большой, значительно превышающей требуемую погрешность определения положения оптимума, и выполняется грубый поиск. В районе оптимума поиск производится с меньшим шагом.

Задается начальное значение параметра y₀ = a и вычисляется I₀=I(y₀). Задаются начальный шаг поиска h и кратность k уменьшения шага в районе оптимума. Производится поиск максимума I(y) из начальной точки y = y₀ по алгоритму

y^(j+1)=y^(j)+h^(j+1);

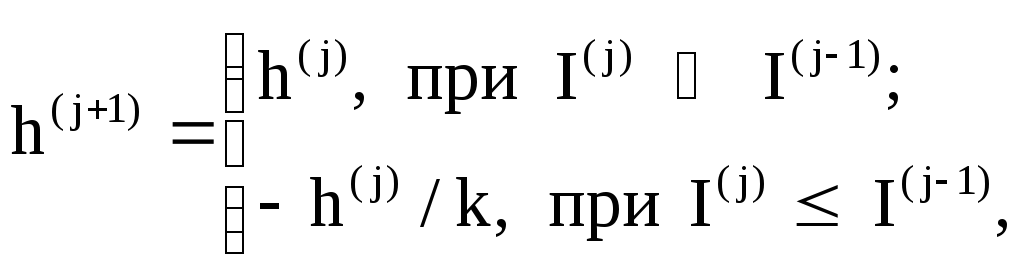(25)

где j - номер шага.

По этому алгоритму поиск из начальной точки y = y₀ осуществляется с постоянным шагом h. После каждого шага вычисляется значение критерия I(y), оно сравнивается с предыдущим значением и в случае улучшения критерия шаги продолжаются до тех пор, пока очередной шаг не окажется неудачным. После этого поиск максимума продолжается из последней точки в обратном направлении с шагом в k раз меньше прежнего. Эта процедура поиска продолжается до тех пор, пока не будет выполнено условие

 h   ,

где  - заданная погрешность определения оптимума.

4.3. Метод дихотомии

Этот метод отыскания экстремума применим для класса унимодальных функций. Идея метода проста - делить интервал [a, b], где расположен оптимум I(y), пополам

y₀ = (a + b)/2

и отбрасывать часть, где оптимума заведомо быть не может. С этой целью достаточно вычислить показатель качества I(y) в точках y₀  d, отстоящих друг от друга на расстояние 2d < , где  - заданная погрешность определения оптимума. По двум вычисленным значениям I(y₀ - d) и I(y₀ + d), в силу унимодальности функции I(y), легко установить новый интервал неопределенности по следующим условиям (при поиске максимума):

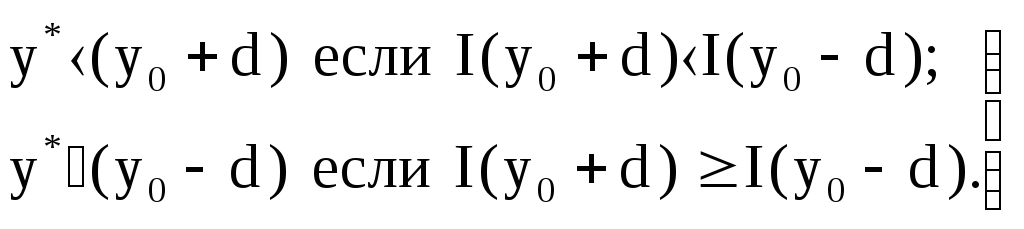(26)

Таким образом, в результате двух вычислений I(y) промежуток, где содержится оптимум, сокращается почти вдвое. Следующая пара измерений проводится в районе середины нового интервала неопределенности [a, y₀ + d] или [y₀ - d, b] в зависимости от того, какое из условий (26) выполняется.

Аналогично производятся последующие шаги поиска до тех пор, пока на k-ом шаге после 2k измерений I(y) длина интервала неопределенности l_k = (b-a)/2k, где находится оптимум, не станет меньше или равен , т. е. l_k.

4.4. Метод золотого сечения

В геометрии золотым сечением называется такое деление отрезка на две неравные части, при котором отношение всего отрезка к большей части равнялось отношению большей части к меньшей.