№1. Элементная схема САУ.

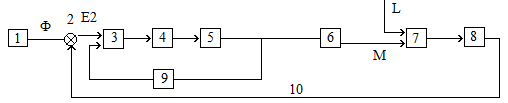
1 – Задающий элемент. Служит для создания сигнала определенной физической природы пропорционального заданному значению регулируемой величины.

2 – Элемент сравнения. Используется для сравнения заданного и измеренного значения регулируемой величины с цель. Получения ошибки управления E(t). Ошибка управления может быть статической и динамической. Статическая ошибка E(∞) – ошибка после окончания переходного процесса (в установившимся режиме).

3 – Функциональный блок. Используется для получения сигнала в соответствии с определенным законом (вычислительное устройство).

4 – Усилитель.

5 – Исполнительный механизм. Для перемещения регулирующего органа 6

6 – Регулирующий орган. Служит для изменения подачи энергии или вещества в объект. На его выходе сигнал m. m(t) – положение регулирующего органа, определяет величину управляющего воздействия. Предназначен для компенсации возмущающего воздействия λ.

7 – Объект регулирования. Устройство или процесс состояние, которого характеризуется одной или несколькими переменными φ.

8 – Измеритель. Служит для преобразования измеренной регулируемой величины сигнала физической природы удобный для дистанционной передачи.

9 – Внутренняя обратная связь. Предназначается для придания системе требуемых статических или динамических свойств.

10 – Главная обратная связь.

λ – возмущающее воздействие, которое стремится нарушить требуемую функциональную связь между переменными характеризующими состояние системы. – задача (цель) управления

№2. Классификация САУ.

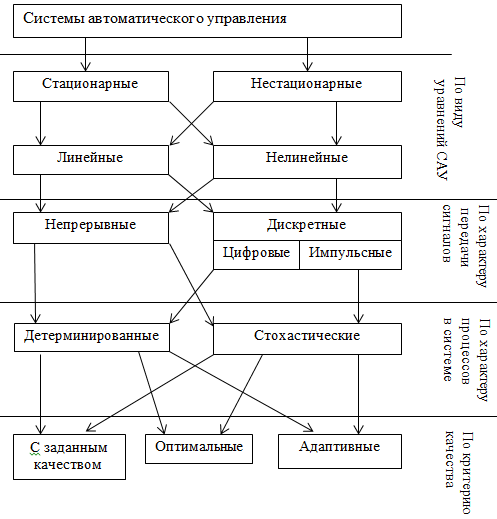
Стационарные системы — параметры объекта не меняются во времени. Нестационарные — наоборот.

Линейные — если зависимость выходной величины от входной по линейному закону.

Непрерывные — величины изменяются непрерывно во времени.

Детерминированные — системы с жёсткой функциональной связью.

Схоластические — меняются случайно.

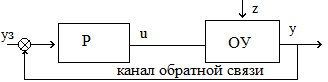
№3. Замкнутая и разомкнутая система. Принципы управления. Комбинированное управление.

Сущность принципа разомкнутого управления заключается в жестко заданной программе управления. То есть управление осуществляется «вслепую», без контроля результата, основываясь лишь на заложенной в САУ модели управляемого объекта. Примеры таких систем : таймер, блок управления светофора, автоматическая структура полива газона, автоматическая стиральная машина и т. п.

В замкнутых структурах автоматического регулирования управляющее воздействие формируется в непосредственной зависимости от управляемой величины. Связь входа структуры с его выходом называется обратной связью. Сигнал обратной связи вычитается из задающего воздействия. Такая обратная связь называется отрицательной.

1. Принцип разомкнутого регулирования:

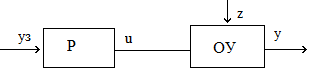уз – желаемый алгоритм функционирования.

Пример: электростат подает температуру на определенное время.

Часть ОУ, которая преобразует управляемую величину в пропорциональную ей величину, удобную для использования в САУ, называют чувствительным элементом (ЧЭ). Физическую величину на выходе ЧЭ называют выходной величиной ОУ. Как правило, это электрический сигнал (ток, напряжение) или механическое перемещение. В качестве ЧЭ могут использоваться термопары, тахометры, рычаги, электрические мосты, датчики давления, деформации, положения и т.п. Физическую величину на входе управляющего органа ОУ называют входной величиной ОУ.

Управляющее воздействие u(t) - это воздействие, прикладываемое к УО объекта с целью поддержания требуемых значений управляемой величины. Оно формируется устройством управления (УУ). Ядром УУ является исполнительный элемент, в качестве которого может использоваться электрические или поршневые двигатели, мембраны, электромагниты и т.п.

Задающим устройством (ЗУ) называется устройство, задающее программу изменения управляющего воздействия, то есть формирующее задающий сигнал u_о(t). В простейшем случае u_о(t)=const. ЗУ может быть выполнено в виде отдельного устройства, быть встроенным в УУ или же вообще отсутствовать. В качестве ЗУ может выступать кулачковый механизм, магнитофонная лента, маятник в часах, задающий профиль и т.п. Роль УУ и ЗУ может исполнять человек. Однако это уже не САУ. В нашем примере УУ является кулачковый механизм, перемещающий движок реостата согласно программе, которая задается профилем кулачка.

Условия работоспособности такой системы:

• Незначительность или полное отсутствие помех

• Достаточность информации о свойствах объекта и неизменность этих свойств в процессе работы.

2. Принцип компенсации (управление по возмущению)

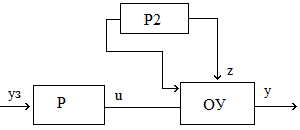Недостаток: все помехи компенсировать нельзя, поэтому выбирают основную помеху.

Реализуется также принцип разомкнутого управления

Компенсируемая помеха должна быть хорошо изучена.

Если возмущающий фактор искажает выходную величину до недопустимых пределов, то применяют принцип компенсации (P2 -корректирующее устройство).

Пусть y_о - значение выходной величины, которое требуется обеспечить согласно программе. На самом деле из-за возмущения f на выходе регистрируется значение y. Величина e = y_о - y называется отклонением от заданной величины. Если каким-то образом удается измерить величину f, то можно откорректировать управляющее воздействие u на входе ОУ, суммируя сигнал УУ с корректирующим воздействием, пропорциональным возмущению f и компенсирующим его влияние.

Достоинство принципа компенсации: быстрота реакции на возмущения. Он более точен, чем принцип разомкнутого управления. Недостаток: невозможность учета подобным образом всех возможных возмущений.

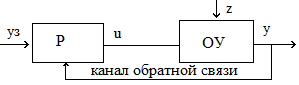
3. Принцип замкнутого управления:

Здесь управляющее воздействие корректируется в зависимости от выходной величины y(t). И уже не важно, какие возмущения действуют на ОУ. Если значение y(t) отклоняется от требуемого, то происходит корректировка сигнала u(t) с целью уменьшения данного отклонения. Связь выхода ОУ с его входом называется главной обратной связью (ОС).

Частный случай:

В частном случае (рис.8) ЗУ формирует требуемое значение выходной величины y_о(t), которое сравнивается с действительным значением на выходе САУ y(t). Отклонение e = y_о-y с выхода сравнивающего устройства подается на вход регулятора Р, объединяющего в себе УУ, УО, ЧЭ.Еслиe0, то регулятор формирует управляющее воздействие u(t), действующее до тех пор, пока не обеспечится равенство e = 0, или y = y_о. Так как на регулятор подается разность сигналов, то такая обратная связь называется отрицательной, в отличие от положительной обратной связи, когда сигналы складываются.

Недостатком принципа обратной связи является инерционность системы. Поэтому часто применяют комбинацию данного принципа с принципом компенсации, что позволяет объединить достоинства обоих принципов: быстроту реакции на возмущение принципа компенсации и точность регулирования независимо от природы возмущений принципа обратной связи.

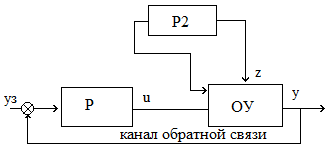4. Комбинированный вид: Управление по отклонению и возмущению.

№4. Математическое описание САУ.

Математическое описание САУ включает построение моделей процессов, протекающих как в самой

системе, так и в ее элементах. Математическое описание САУ осуществляют, описывая математическими

соотношениями все алгоритмические элементы системы и их взаимодействие между собой и с внешней

средой.

Таким образом под математическим описанием ( мат моделью) подразумевают совокупность

(систему) уравнений и граничных условий, которые в количественной форме описывают зависимость

выходных величин от входных в установившемся и переходном режимах. В связи с этим различают два рода

уравнений САУ: статики и динамики.

В общем случае уравнения динамики являются дифференциальными или интегрально-

дифференциальными и полностью описывают поведение системы (элемента) в переходном режиме.

Уравнения статики (установившийся режим – режим с постоянной скоростью или состояние покоя)

представляют собой дифференциальное уравнение нулевого порядка, т.е. алгебраическое уравнение.

Статической характеристикой элемента (системы) называется зависимость выходной величины или

скорости ѐѐ изменения от входной от входной величины в установленном режиме.

Уравнение1:

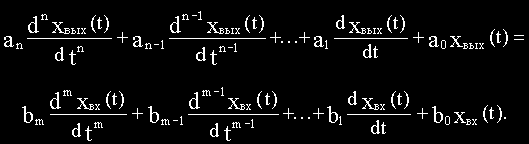
Каждый элемент САУ в общем случае описывается дифференциальным уравнением вида (1). Следовательно, при выводе дифференциального уравнения системы в целом необходимо совместно решить несколько дифференциальных уравнений высших порядков.

Преобразование дифференциальных уравнений по Лапласу позволяет свести эту задачу к решению системы алгебраических уравнений. Определив из алгебраических уравнений изображение X(p) искомой функции x(t), определяющей переходной процесс в системе, находят эту функцию, пользуясь таблицами оригиналов и изображений или по известным формулам обратного преобразования Лапласа.

Кроме того, преобразование дифференциального уравнения по Лапласу дает возможность ввести понятие передаточной функции.

(a_npⁿ+a_n-1p^n-1+...+a₁p+a₀)Xвых(p)=(b_mp^m+b_m-1p^m-1+...+b₁p+b₀)X_вх(p).

Определим из этого уравнения отношение изображения выходной величины к изображению входной:

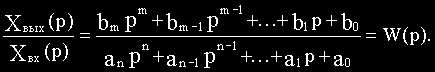(2.4)

Отношение изображения выходной величины элемента (или системы) к изображению его входной величины при нулевых начальных условиях называется передаточной функцией элемента (или системы).

Передаточная функция W(p) является дробно-рациональной функцией комплексной переменной р:

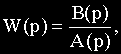
где A(p)=a_npⁿ+a_n-1p^n-1+...+a₁p+a₀- полином степени n,

B(p)=b_mp^m+b_m-1p^m-1+...+b₁p+b₀- полином степени m.

Из определения передаточной функции следует, что:

X_вых(p)=X_вх(p)W(p).

Передаточная функция является основной формой математического описания объектов в теории автоматического управления и так как она полностью определяет динамические свойства объекта, то первоначальная задача расчета САУ сводится к определению передаточной функции.

№5. Переходные процессы в САУ. Виды переходных процессов.

Исследование свойств звеньев или систем управления может быть проведено по реакции на одинаковые входные сигналы. В качестве ти­повых входных сигналов используются различные функции.

а) ступенчатая функция, аналитическое выражение которой можно записать так:

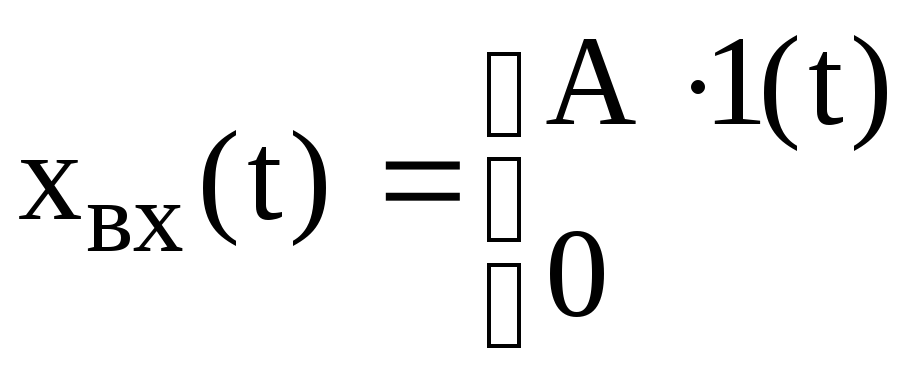
Функция называется единичной ступенчатой функцией. Реакция звена или системы управления на единичную ступенчатую функцию называется переходной функцией. Она может быть получена путем решения дифференциального уравнения при единичном ступенчатом входном воздействии. Если реакция звена или системы на ступенча­тое входное воздействие получена экспериментально, то она называется кривой разгона.

б) импульсная функция. Является производной ступенчатой функции и обозначается . Она представляет импульс бесконечно большой величины и бесконечно малой длительности интеграл от которой. Реально такой импульс иметь нельзя, одна­ко являясь математической идеализацией, он облегчает исследование САУ. Изображениеможно получить с помощью предельного перехода для изображения импульсного сигнала, когда его амплитуда стремится к бесконечности, а длительность к нулю.

- переходная функция звена или

системы, имеющей передаточную функцию .

Передаточная функция звена или системы есть отношение операторных изображений выходной и входной величин при нулевых начальных условиях.

в) гармоническая функция. Она может быть задана в веществен­ной или комплексной форме:

, или ,

где -угловая частота;- период колебаний.

Весьма удобной при исследовании CАУ оказывается комплексная форма задания гармонической функции:

.

При этом интерес представляет способность звена или системы воспроизводить входной сигнал на выходе, т.е. частное реше­ние неоднородного дифференциального уравнения которое также представляет гармоническую функцию, но с амплитудой и фазой, отличной от входного воздействия. Амплитуда и фаза выходной величины зависят от частоты и параметров системы. Поэтому исследование реакции звена или системы на гармоническое воздействие приводит к понятию частотных характеристик.

Формально амплитудно-фазовая характеристика может бытьполучена путем замены в передаточной функциина. Действительно, дифференциальное уравнение (1) в операторной форме имеет вид:

,

откуда передаточная функция

,

амплитудно-фазовая характеристика

.

№6. Переходные процессы в САУ. Качество переходных процессов.

Переходная функция системы оценивается с помощью совокупности характеристик, называемых показателями

качества переходного процесса. Принято использовать следующие стандартные показатели качества

переходного процесса, отражённые на типичном графике 1 переходного процесса в следящей системе со

ступенчатым задающим воздействием (рис. 4.5.2):

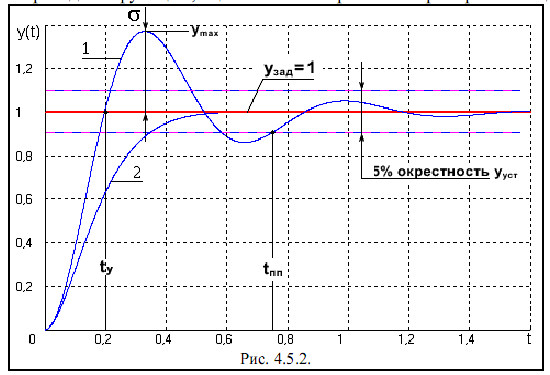
tпп - время переходного процесса, по истечении которого отклонение управляемой величины y(t) относительно заданного значения по абсолютному значению становится (и остается в дальнейшем) меньше определенной заданной величины . Обычно принимается = δ , δ = 0.05. Время регулирования характеризует быстроту затухания переходного процесса.

tу - время установления, промежуток времени, за который управляемая величина в первый раз достигает своего установившегося значения, характеризует скорость процесса управления.

- установившаяся ошибка (статическая точность, = e(∞) =1- .). Если =0, то система астатическая.

σ% - относительное перерегулирование (σ = (ymax-yзад)/yзад). Обычно требуют, чтобы значение σ было менее 18%. Перерегулирование характеризует колебательные свойства процессов. При нулевом значении σ процесс носит монотонный характер (график 2 на рис. 4.5.2), а при достаточно больших σ приближается к незатухающему колебательному движению.

n - число колебаний за время переходного процесса (≤3шт.).

№7. Классификация САУ. Стабилизирующие и программные САУ.

Стабилизирующие САУ. Алгоритм функционирования системы: поддержание с необходимой точностью постоянства (стабилизация) одной или нескольких управляемых величин при произвольно меняющихся возмущающих воздействиях. Задающее воздействие системы – постоянная величина, т.е. a(t) = const.

Пример, стабилизирующая система скорости вращения электродвигателя.

Нагрузка управляемого объекта в стабилизирующих системах обычно является основным возмущающим воздействием, наиболее резко влияющим на управляемую величину.

Программные САУ. Алгоритм функционирования системы: изменение управляемой величины с необходимой точностью в соответствии с заранее составленной программой. Задающее воздействие системы a(t) = Fп(t), где Fп(t) – программа, заранее известная функция времени.

Программную систему можно рассматривать как стабилизирующую систему, в которой задача стабилизации усложняется задачей изменения управляемой величины по заданной программе. Изменение управляемой величины по программе достигается добавлением к стабилизирующей системе программного устройства (ПУ), изменяющего задающее воздействие a(t) во времени по определенному закону.

Пример, системы программного управления станками; металлургическими, химическими процессами.

№8. Классификация САУ. САУ слежения и программные.

Программные САУ. Алгоритм функционирования системы: изменение управляемой величины с необходимой точностью в соответствии с заранее составленной программой. Задающее воздействие системы a(t) = Fп(t), где Fп(t) – программа, заранее известная функция времени.

Программную систему можно рассматривать как стабилизирующую систему, в которой задача стабилизации усложняется задачей изменения управляемой величины по заданной программе. Изменение управляемой величины по программе достигается добавлением к стабилизирующей системе программного устройства (ПУ), изменяющего задающее воздействие a(t) во времени по определенному закону.

Пример, системы программного управления станками; металлургическими, химическими процессами.

Следящие САУ. Алгоритм функционирования системы: изменение управляемой величины с необходимой точностью в соответствии с заранее неизвестной функцией времени, определяемой задающим воздействием: a(t) = F(t), где F(t) – заранее неизвестная функция времени. Т.о. следящая, как и программная сис-ма, воспроизводит задающее воздействие.

Пример, антенна радиолокатора поворачивается следуя за самолетом.

Задающие воздействия и управляемые величины следящих систем могут иметь разнообразный характер по своей физической природе. Причем управляемая величина по своей физической природе может отличаться от задающего воздействия.

№9. Классификация САУ по характеру внутренних динамических процессов.

Основными признаками деления автоматических систем па большие классы по характеру внутренних динамических процессов являются следующие:

• непрерывность или дискретность (прерывистость) динамических процессов во времени;

• линейность или нелинейность уравнений, описывающих динамику процессов управления.

По первому признаку автоматические системы делятся на системы непрерывного действия, системы дискретного действия (импульсные и цифровые) и системы релейного действия.

По второму признаку каждый из указанных классов, кроме релейного, делится на системы линейные и нелинейные. Системы же релейного действия относятся целиком к категории нелинейных систем.

Системой непрерывного действия или непрерывной системой называется такая система, в каждом из звеньев которой непрерывному изменению входной величины во времени соответствует непрерывное изменение выходной величины. При этом закон изменения выходной величины во времени может быть произвольным, в зависимости от формы изменения входной величины и от вида уравнения динамики (или характеристики) звена.

Чтобы автоматическая система в целом была непрерывной, необходимо прежде всего, чтобы статические характеристики всех звеньев системы были непрерывными.

Системой дискретного действия, или дискретной системой называется такая система, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина изменяется не непрерывно, а имеет вид отдельных импульсов, появляющихся через некоторые промежутки времени.

Системой релейного действия или релейной системой называется такая система, и которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина в некоторых точках процесса, зависящих от значения входной величины, изменяется скачком. Такое звено называется релейным звеном. Статическая характеристика релейного звена имеет точки разрыва.

Линейной системой называется такая система, поведение всех звеньев которой вполне описывается линейными уравнениями (алгебраическими и дифференциальными или разностными). Для этого необходимо прежде всего, чтобы статические характеристики всех звеньев системы были линейными, т. е. имели вид прямой линии.

Нелинейной системой называется такая система, в которой хотя бы в одном звене нарушается линейность статической характеристики или же имеет место любое другое нарушение линейности уравнений динамики звена (произведение переменных или их производных, корень, квадрат или более высокая степень переменной, любая другая нелинейная связь переменных и их производных).

№10. Системы непрерывного действия.

Системой непрерывного действия или непрерывной системой называется такая система, в каждом из звеньев которой непрерывному изменению входной величины во времени соответствует непрерывное изменение выходной величины. При этом закон изменения выходной величины во времени может быть произвольным, в зависимости от формы изменения входной величины и от вида уравнения динамики (или характеристики) звена.

№11. Системы релейного действия.

Системой релейного действия или релейной системой называется такая система, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина в некоторых точках процесса, зависящих от значения входной величины, изменяется скачком. Такое звено называется релейным звеном. Статическая характеристика релейного звена имеет точки разрыва.

№12. Линейные системы.

Линейной системой называется такая система, поведение всех звеньев которой вполне описывается линейными уравнениями (алгебраическими и дифференциальными или разностными). Для этого необходимо прежде всего, чтобы статические характеристики всех звеньев системы были линейными, т. е. имели вид прямой линии.

Если динамика всех звеньев системы описывается обыкновенными линейными дифференциальными (и линейными алгебраическими) уравнениями с постоянными коэффициентами, то систему называют обыкновенной линейной системой. Если в уравнении динамики какого-либо звена линейной системы имеется хотя бы один или несколько переменных во времени коэффициентов, то получается линейная система с переменными параметрами.

Если какое-либо звено описывается линейным уравнением в частных производных (например, имеют место волновые процессы в трубопроводе или в электрической линии), то система будет линейной системой с распределенными параметрами. В отличие от этого обыкновенная линейная система является системой с сосредоточенными параметрами. Если динамика какого-либо звена системы описывается линейным уравнением с запаздывающим аргументом (т. е. звено обладает чисто временным запаздыванием или временной задержкой передачи сигнала, то система называется линейной системой с запаздыванием. Динамика линейных импульсных систем описывается линейными разностными уравнениями.

№13. Программное управление.

Одной из задач системы автоматического управления является, как уже говорилось, поддержание требуемого значения управляемой величины у или изменение ее по определенной программе, которая либо заранее задается, либо поступает извне во время эксплуатации системы в зависимости от некоторых условий.

Программы могут быть временными (задаваемыми во времени):

или параметрическими (задаваемыми в текущих координатах):

Примером временной программы может служить программа изменения управляемой величины, обеспечивающая правильный режим начального «разгона» объекта при пуске его в ход до наступления режима нормальной эксплуатации, в котором объект затем будет работать длительное время.

Примером параметрической программы может служить задание требуемого переменного значения высоты полета у при снижении летательного аппарата, но не во времени, а в зависимости от текущего значения пройденного пути s, чтобы снизиться в определенную точку независимо от времени протекания этого процесса.

№14. Линейные алгоритмы управления (пропорциональные, по производным, пропорционально – дифференциальные, интегральное, изодромное, ПИД)

1. Пропорциональное управление. В случае пропорционального управления алгоритм управления имеет вид

, когда ошибка становится равной нулю, управляющее воздействие будет продолжать действовать в прежнем направлении, вынуждая ее вновь увеличиваться, изменив знак. В результате процесс в системе может стать слишком колебательным и даже расходящимся.

2.             Управление по производным. При управлении по первой производной от ошибки осуществляется зависимость

т. е. управляющее устройство реагирует не на саму ошибку, а на скорость ее изменения (рис. 2.7, б), и поэтому действует с упреждением, стремясь не допустить появления ошибки.

Управление по производной не имеет самостоятельного значения, так как в установившемся состоянии, когда ошибка постоянна, производная от ошибки равна нулю и управление прекращается. Однако оно может играть весьма большую роль в переходных процессах и вообще в динамике в качестве вспомогательного средства, так как такое управление позволяет учитывать не только наличие ошибки, но и тенденцию к росту или уменьшению ошибки. Поэтому управление по производной обычно сочетается с управлением по отклонению:

В некоторых случаях в алгоритм управления могут вводиться производные более высоких порядков — вторая, третья и т. д. Это еще больше улучшает динамические качества системы автоматического управления. Однако в настоящее время техническая реализация производных выше второго порядка встречает значительные трудности.

  3. Интегральное управление. При интегральном управлении осуществляется пропорциональная зависимость между скоростью изменения управляющего-воздействия и ошибкой:

При возникновении ошибки управляющее воздействие накапливается постепенно, запаздывая по отношению к изменению ошибки.

Управление с целью повышения точности системы может осуществляться и по второму интегралу от ошибки по времени:

Однако при этом снижение быстродействия станет еще более заметным.

4. Изодромное управление. При изодромном управлении осуществляется зависимость

Такое управление сочетает в себе высокую точность интегрального управления с большим быстродействием пропорционального управления. В первые моменты времени при появлении ошибки система изодромного управления работает как система пропорционального управления. Это определяется первым слагаемым в правой части алгоритма управления. В дальнейшем система начинает работать как система интегрального управления, так как с течением времени преобладающее значение начинает приобретать второе слагаемое.

5. Пропорционально- интегрально- дифференциальный закон (ПИД):

Постоянные Ти и Тд, соответственно, называют постоянными времени интегрирования и дифференцирования. Регулятор ПИД также обеспечивает астатическое регулирование. Производную dε / dt вводят в закон регулирования для повышения качества процесса регулирования.

6. Пропорционально-дифференциальный регулятор

Связь выходной и входной величин определяется соотношением

(46)

где - постоянная времени дифференцирования.

Передаточная функция имеет вид

(47)

Амплитудно-фазовая характеристика

(48)

На комплексной плоскости представляет прямую, начинающуюся на положительной вещественной оси на расстояниии проходящую параллельно мнимой оси в первом квадранте.

№15. Нелинейные алгоритмы управления (функциональные, логические, оптимизирующие, параметрические)

Важным отличием нелинейных алгоритмов от линейных является то, что они придают системе принципиально новые свойства. Если при линейном алгоритме всегда вырабатывается сигнал, пропорциональный входной переменной или ее производной и т. д., то при нелинейном алгоритме может существенно изменяться сам характер действия системы управления на объект в зависимости от величины входного воздействия.

Функциональные нелинейные алгоритмы управления. Функциональными будем называть такие нелинейные алгоритмы, при которых управляющее воздействие на объект выражается в виде нелинейной функции от отклонения его величины, представляющей собой входную информацию для системы.

Данный класс может содержать в себе как статические, так и динамические нелинейности. Примеры статических нелинейностей:

Примеры динамических нелинейностей в алгоритме управления:

Логические нелинейные алгоритмы управления. Нелинейные законы управления могут иметь иные формы, которые реализуются с помощью не функциональных, а более или менее сложных логических устройств. Будем называть их логическими нелинейными алгоритмами. Логические нелинейные алгоритмы управления могут быть связаны также с изменением структуры системы. Например, при помощи логического устройства можно включать и выключать сигналы управления но первой и второй производным и по интегралу, в зависимости от сочетания значений отклонения управляемой величины x и скорости отклонения ее dx/dt. Если правильно сформировать логику этих переключений, то можно существенно повысить качество работы системы.

Оптимизирующие нелинейные алгоритмы управления. Оптимальной называется автоматическая система, наилучшая в некотором смысле с учетом ограничений, накладываемых на величину управляющего воздействия, координаты, скорости и т. п. 

Часто оптимальный нелинейный алгоритм состоит в переключении управляющего воздействия (при определенных состояниях системы) с одного максимально возможного значения на другие. 

Моменты переключения в целом определяются сложными комбинациями значений нескольких переменных и их производных.

Параметрические нелинейные алгоритмы управления. В предыдущих тинах алгоритмов вводились отклонения управляемой величины от некоторых заданных ее программных значений. При параметрической программе управления алгоритм может выражаться в виде нелинейных функций текущих координат, в которых задается параметрическая программа.

№16. Линеаризация уравнений.

Для упрощения исследований САУ нелинейные дифференциальные уравнения во многих случаях можно приближенно заменить линейными. Процесс преобразования нелинейных уравнений в линейные называют линеаризацией.

Основой возможности линеаризации нелинейных уравнений является выдвинутое И.А.Вышнеградским положение о том, что в течение процесса управления происходят лишь достаточно малые отклонения всех величин от их установившихся значений. Этот метод получил название метода малых отклонений. Математической основой метода малых отклонений является разложение нелинейных функций в ряд Тейлора.

Пусть, например, звено (рис. 3.1, а) какой-нибудь автоматической системы имеет входные величины x1,x2, выходную — х3 и внешнее воздействие, а динамическое уравнение звена имеет произвольный нелинейный вид

Допустим, что установившийся процесс в системе имеет место при некоторых постоянных значениях х1 =х1° ,

х2 = х2° , х3 = х3° и f = f° .Тогда уравнение установившегося состояния для данного звена согласно 3.1) будет

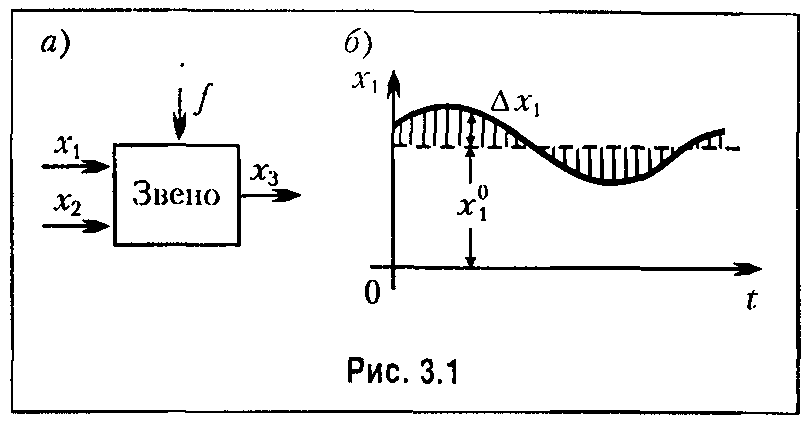
В основе линеаризации нелинейных уравнений лежит предположение о том, что в исследуемом динамическом процессе переменные (в данном случае х1, х2, х3) изменяются так, что их отклонения от установившихся значений х1°,х2° ,x-j ) остаются все время достаточно малыми (рис. 3.1, б).

Обозначим указанные отклонения через ΔX1, ΔX2, ΔX3. Тогда в динамическом процессе

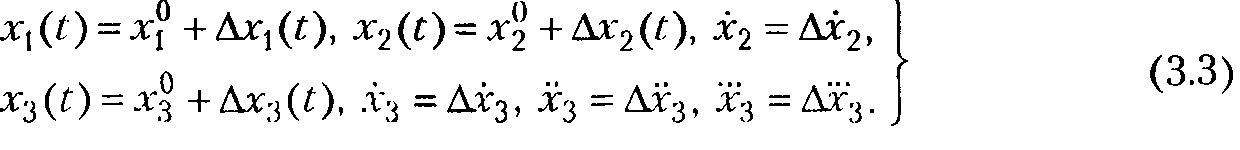
Условие достаточной малости динамических отклонений переменных от некоторых установившихся значений для системы автоматического управления обычно выполняется. Этого требует сама идея работы замкнутой автоматической системы.

№17. Передаточная функция.

Передаточная функция звена или системы есть отношение операторных изображений выходной и входной величин при нулевых начальных условиях.

Передаточная функция линейной стационарной системы управления (системы автоматического регулирования) — отношение изображений (результатов преобразования) выходного и входного сигналов с нулевыми начальными данными.  П. ф. системы определяется только её статическими и динамическими свойствами; результатом её обратного преобразования является импульсная переходная функция, то есть реакция системы на импульсное входное воздействие.  П. ф. сложной системы является комбинацией П. ф. составляющих её звеньев. Для многомерной системы, имеющей несколько входов, могут быть определены П. ф. по всем параметрам состояния и их линейным комбинациям при каждом входном воздействии. П. ф. широко применяются при анализе динамики летательного аппарата и синтезе систем управления, так как позволяют полностью или частично решить ряд задач этого класса с помощью алгебраических операций.  При исследовании динамики летательного аппарата с системами управления, включающими бортовые ЭВМ, используется так называемое Z-преобразование сигналов и соответствующие ему дискретные (импульсные) П. ф. систем и их элементов.

№18. Частотная передаточная_ф-я

Частотная передаточная функция звена есть изображение Фурье его функции веса, т. е. имеет место интегральное преобразование

Частотная передаточная функция может быть представлена в следующем виде:

вещественная и мнимая составляющие частотной передаточной функции.

Модуль частотной передаточной функции находится как отношение модулей числителя и знаменателя. Для рассмотренного выше выражения (4.12)

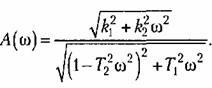
Аргумент или фаза частотной передаточной функции находится как разность аргументов числителя и знаменателя. Для (4.12) имеем:

Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части. Для (4.12)

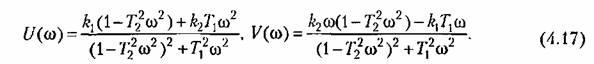
Для наглядного представления частотных свойств звена используются так называемые частотные характеристики.

№ 19. Временные характеристики.

Динамические свойства звена могут быть определены по его переходной функции и функции веса.

Переходная функция, или переходная характеристика, h(t) описывает переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице (рис. 4.3). Такое входное воздействие называется единичной ступенчатой функцией и обозначается x1(t) = 1(t), что соответствует х1 = 0 при t < 0 и х1 = 1 при t > 0.

Ступенчатая функция представляет собой распространенный вид входного воздействия в автоматических системах. К такому виду сводятся мгновенное изменение нагрузки электрического генератора, мгновенное возрастание нагрузки на валу двигателя, мгновенный поворот командной оси следящей системы и т. п.

Функция веса w(t) представляет собой реакцию звена на единичную импульсную функцию, поданную на его вход.

Единичная импульсная функция или дельта-функция представляет собой производную от единичной ступенчатой функции: δ(t) = 1' (t). Дельта-функция тождественно равна нулю повсюду, кроме точки t = 0, где она стремится к бесконечности.

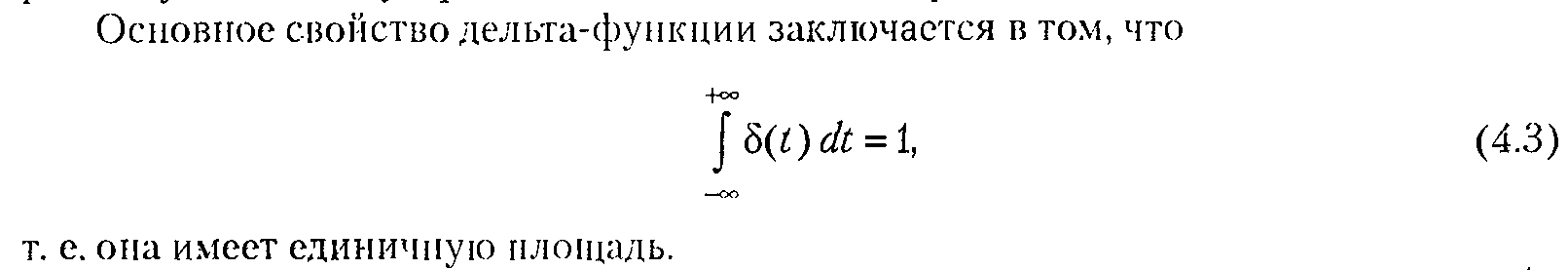
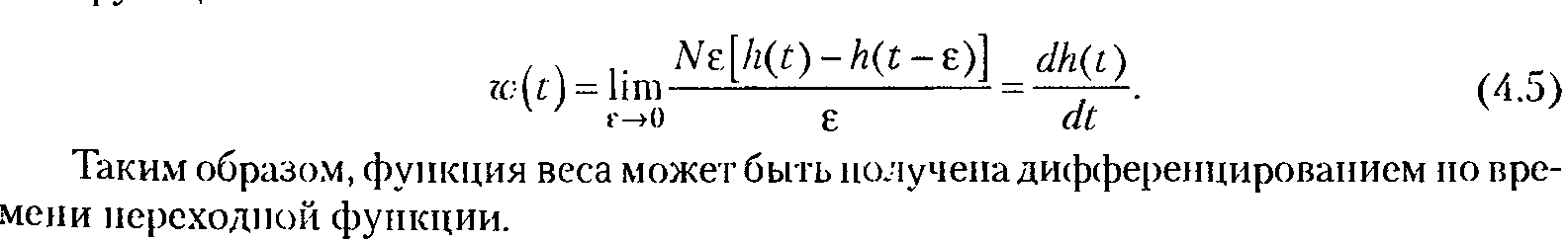
№20. Динамические звенья и их характеристики.

По динамическим свойствам независимо от физической природы простейшие (неделимые) звенья подразделяются на усилительные (масштабные), апериодические, интегрирующие, дифференцирующие, ко­лебательные, звенья чистого запаздывания. На эти звенья можно разложить систему любой сложности, а также синтезировать из них желае­мую систему любой сложности.

Основными характеристиками звеньев являются: дифференциальное уравнение, передаточная и переходная функции, амплитудно-фазовая характеристика, логарифмические частотные характеристики (ЛАЧХ, ЛФЧХ).

Усилительные звенья

Особенностью усилительных звеньев является их практическая безинерционность, т.е. выходная величина в точности воспроизводит входную в измененном масштабе (усилители, потенциометры, редукто­ры, рычаги и т.д.): , где- коэффициент усиления, который может быть больше и меньше единицы и иметь размерность, согласующую выходную и входную вели­чины.

Передаточная функция усилительного звена:

.

Амплитудно-фазовая характеристика

не зависит от частоты.

На комплексной плоскости представляем точку на положительной вещественной оси, удаленную от начала координат за величину .

Если на вход звена подается ступенчатый единичный сигнал, то на выходе получается переходная функция в виде ступенчатого сигнала величины .

Апериодическое звено

Его называют инерционным звеном первого порядка, одноёмкостным статическим звеном. Дифференциальное уравнение его запишем так: , где- постоянная времени, имеющая размерность времени,-коэффициент усиления.

Передаточная функция звена будет такой:

. (6)

Сделав в передаточной функции (6) замену , получим:

.

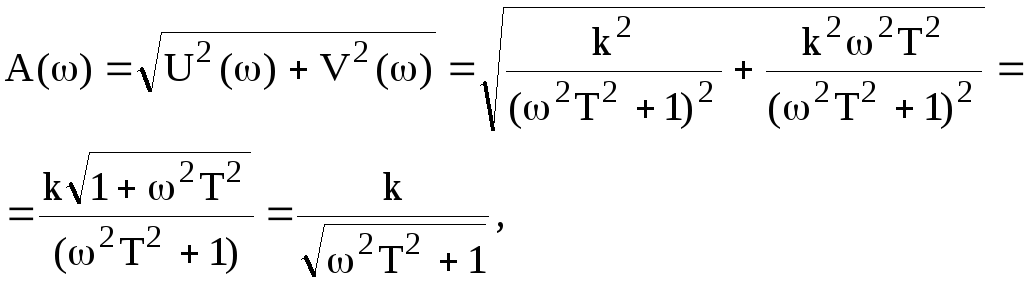
где - амплитудно-частотная характеристика.

АФХ апериодического звена представляет окружность с центром на вещественной оси на расстоянии и радиусом. Действительно,,

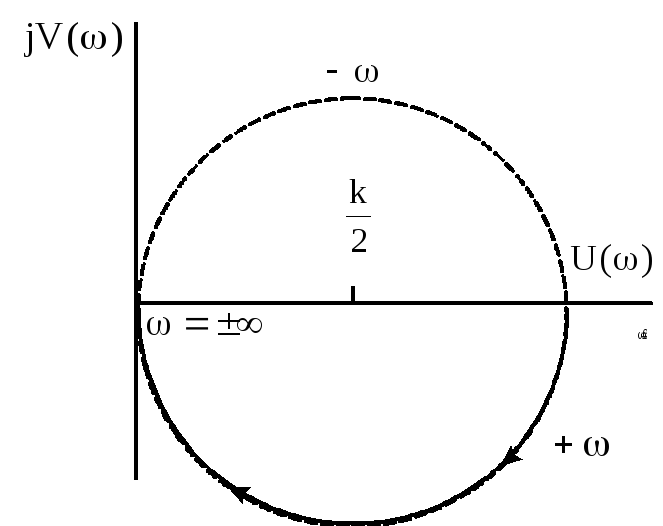
Рисунок 1 - АФХ апериодического звена

Интегрирующее звено

Выходная величина интегрирующего звена равна интегралу по времени от входной, , или.

Передаточная функция звена равна:

; .

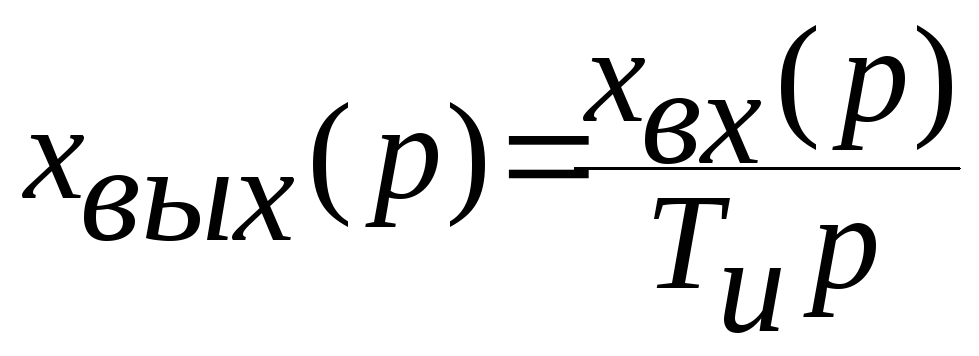, где - постоянная времени интегрирования, численно равна време­ни, через которое значение выходной величины станет равно входному воздействию.

Амплитудно-Фазовая характеристика интегрирующего звена по­лучается из уравнения заменой :

.

Дифференцирующее звено

Для идеального (физически не реализуемого) дифференцирующего звена выходная величина пропорциональна скорости изменения входной

, где - постоянная времени дифференцирования.

Если на вход такого звена подавать сигнал, изменяющийся с постоянной скоростью, то выходной сигнал будет постоянен. Время, за которое входной сигнал, изменяясь с постоянной скоростью от нуля до единицы, обеспечит выходной сигнал равный единице, называется постоянной времени дифференцирования идеального дифференцирующего звена.

Переходная функция дифференцирующего звена представляет бесконечно большой амплитуды и бесконечно малой длительности импульс, площадь которого равна .

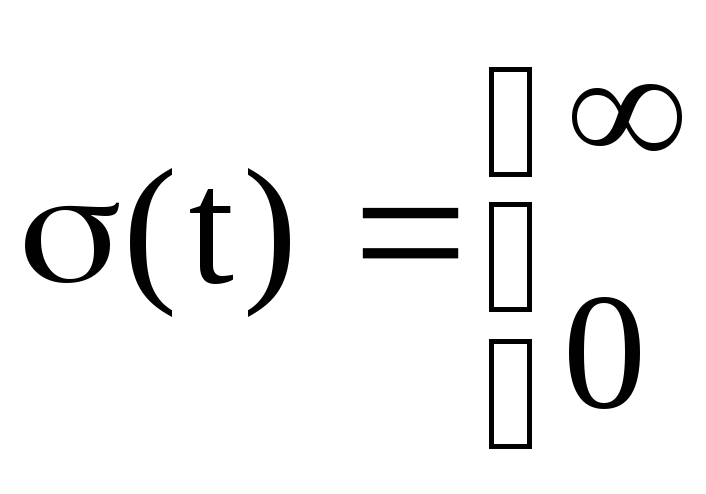, гдепри.

Передаточная и амплитудно-фазовая характеристики дифференцирующего звена получаются из выражения и равны:

; . (15)

Легко видеть, что АФХ дифференцирующего звена совпадает с мнимой осью. Она начинается в начале координат при и устремляется в верхнюю полуплоскость при.

Колебательное звено

Статические и динамические свойства колебательного звена описываются дифференциальным уравнением второго порядка вида

, где ,- постоянные времени, имеющие размерность времени. В операторном виде уравнение запишем так:

,

откуда передаточная функция

.

Для получения переходной функции необходимо решить уравнение при единичном входном воздействии. При этом решение будет зависеть от вида свободной составляющей, определяемой корням характеристического уравнения

, где .

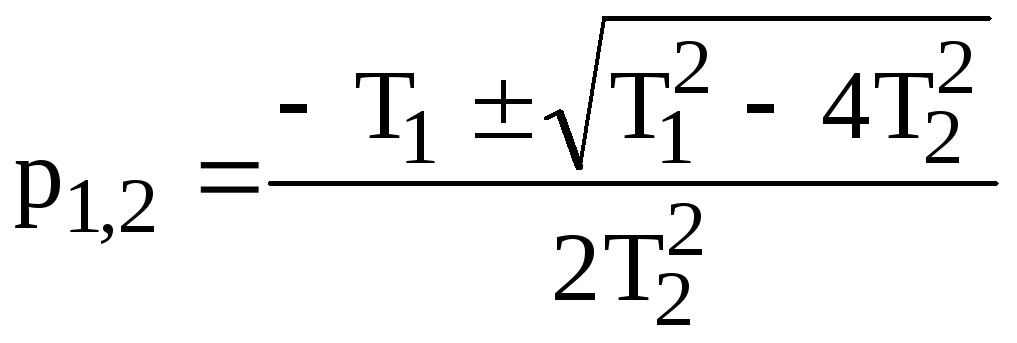Рассмотрим вид переходной функции для различных видов корней характеристического уравнения.

а) . В этом случае корнибудут вещественными отрицательными,

.

б) .,

.

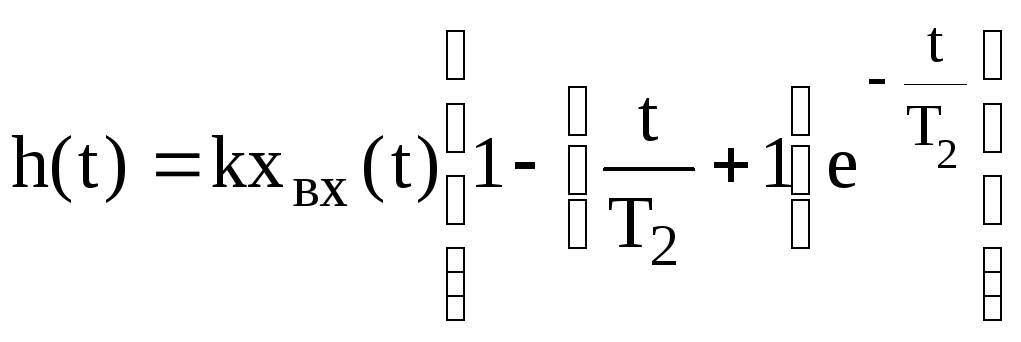в) ,

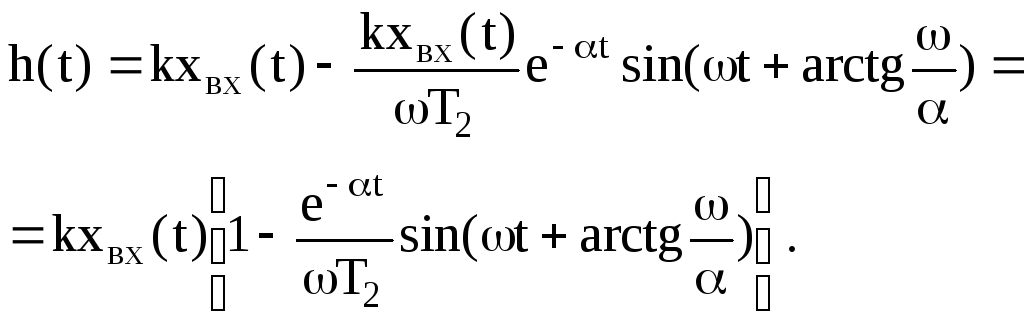
Амплитудно-фазовая характеристика колебательного звена получается из выражения заменой :

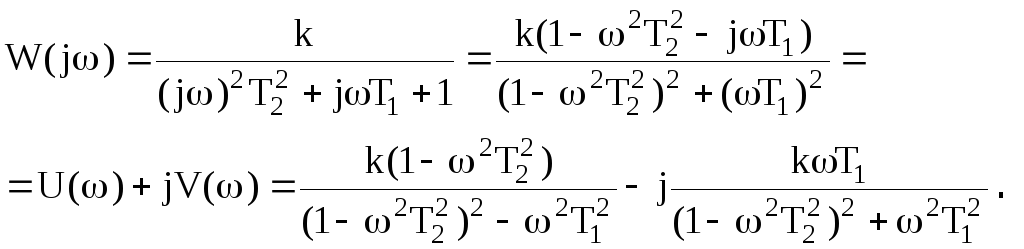
Если корни характеристического уравнения вещественные отрицательные, то передаточную функцию (18) можно записать так:

. Это эквивалентно включению последовательно двух апериодических звеньев.

Звено чистого запаздывания

Уравнение, связывающее выходную и входную величины:

.

Передаточная функция звена

.

Амплитудно-фазовая характеристик

.

АФХ представляет на комплексной плоскости окружность единичного радиуса с центром в начале координат.

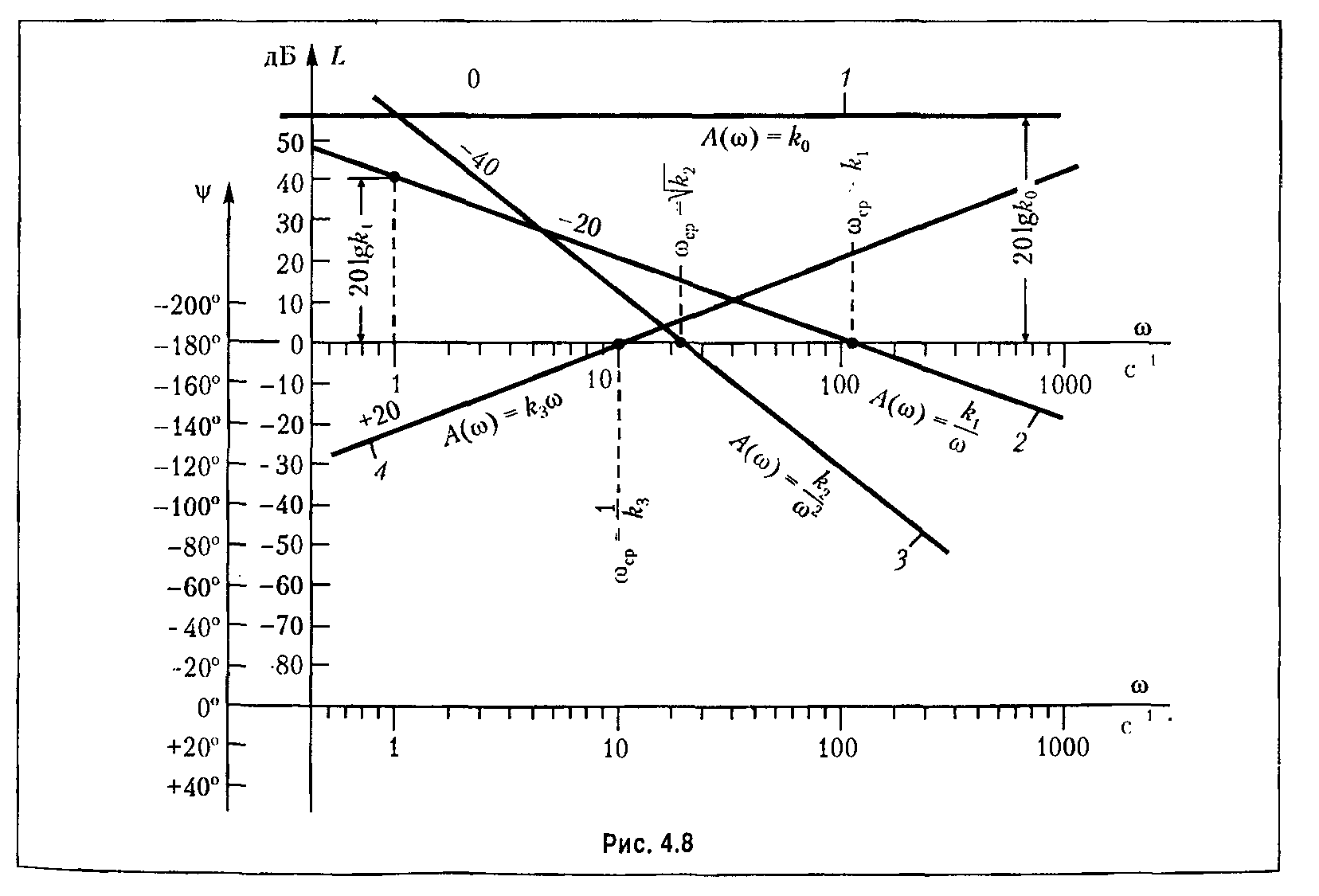
№21. Логарифмические частотные характеристики.

Логарифмические частотные характеристики ( л. ч. х.) включают и себя построенные отдельно на одной плоскости логарифмическую амплитудную характеристику (л. а. х.) и логарифмическую фазовую характеристику (л. ф. х.). Для построения л. а. х. находится величина

Эта величина выражается в децибелах.

Для построения л. а. х. и л. ф. х. используется стандартная сетка. По оси абсцисс откладывается угловая частота в логарифмическом масштабе, т. е. наносятся отметки, соответствующие lg ω, а около отметок пишется само значение частоты ω в рад/с.

По оси ординат откладывается модуль в децибелах (дБ). Для этой цели на ней наносится равномерный масштаб. Ось абсцисс должна проходить через точку 0 дБ, что соответствует значению модуля Л (?) = 1,так как логарифм единицы равен нулю. Ось ординат может пересекать ось абсцисс (ось частот) в произвольном месте.

Следует учесть, что точка ? = 0 лежит на оси частот слева в бесконечности, так как lg 0 = -оо. Поэтому ось ординат проводят так, чтобы справа от нее можно было показать весь ход л. а. х.

Для построения л. ф. х. используется та же ось абсцисс (ось частот). По оси ординат откладывается фаза в градусах в линейном масштабе. Для практических расчетов, как это будет ясно ниже, удобно совместить точку нуля децибел с точкой, где фаза равна -180°. Отрицательный сдвиг по фазе откладывается по оси ординат вверх, а положительный — вниз.

Главным достоинством логарифмических амплитудных частотных характеристик является возможность построения их во многих случаях практически без вычислительной работы. Это особенно проявляется в тех случаях, когда частотная передаточная функция может быть представлена в виде произведения сомножителей. Тогда результирующая л. а. х. может быть приближенно построена в виде так называемой асимптотической л. а. х„ представляющей собой совокупность отрезков прямых линий с наклонами, кратными величине 20 дБ/дек.

№22. Составление передаточных функций по дифференциальным уравнениям САУ.

Применив к дифференциальному уравнению

преобразование

Лапласа, получим:

где x(p) – преобразование Лапласа выходного сигнала системы; g(p) – преобразование Лапласа входного сигнала. Часто x(p) и g(p) называют изображениями сигналов x(t) и g(t). Введем обозначение

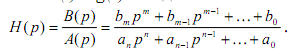
Тогда можем записать

Данное уравнение связывает между собой изображения выходного и входного сигналов системы. Функция H(p) не зависит от входного воздействия g(t), а определяется параметрами самой системы ai и bi

. Эту функцию называют передаточной функцией системы. Передаточная функция равна отношению изображения выходного сигнала к изображению входного сигнала

№23. Общие положения об устойчивости.

Система автоматического управления будет называться устойчивой, если выведенная из состояния равновесия и предоставленная самой себе она возвращается в исходное состояние, т.е. при снятии внешнего воздействия САУ возвращается в то состояние, в котором она находилась до возмущения.

Известно, что вид переходного процесса в САУ определяется суммой двух составляющих - свободной и вынужденной. Поскольку вынужденная составляющая определяется внешним воздействием, а устойчивость линейной САУ зависит от ее поведения после снятия внешнего возмущения, то можно сделать следующий вывод: устойчивость линейной САУ не зависит от внешнего воздействия, а определяется видом свободной составляющей переходного процесса.

Свободная составляющая переходного процесса находится как общее решение линейного однородного уравнения

,

где - отклонение регулируемой величины от исходного установившегося состояния.

Поскольку решение уравнения (2.1) определяется корнями характеристического уравнения

, (2.2)

то, следовательно, устойчивость САУ будет зависеть от вида корней уравнения (2.2).

В случае различных вещественных корней

.

Система автоматического управления будет устойчива, если

При ; нейтральна, если при ; неустойчива, если при .

Свободная составляющая будет стремиться к нулю тогда, когда каждое слагаемое суммы будет стремиться к нулю при . Это условие будет выполняться в таких случаях:

все корни характеристического уравнения (2.2) отрицательные;

все корни имеют отрицательные вещественные части.

Если в характеристическом уравнении (2.2) будет хотя бы один нулевой или пара мнимых сопряжений корней, , и, следовательно, система будет нейтральна (находится на границе устойчивости).

Если хотя бы один корень характеристического уравнения САУ вещественный-положительный или пара комплексно--сопряженных корней имеет положительные вещественные части, то САУ неустойчива.

№24. Алгебраический критерий устойчивости Гурвица.

Если характеристическое уравнение САУ имеет вид (2.2), то система автоматического управления будет устойчива, если при будут положительны все главные диагональные миноры определителя Гурвица до порядка.

Определитель Гурвица составляется следующим образом: по диагонали записывают коэффициенты от до , над диагональю записывают коэффициенты с возрастающим индексом, под диагональю - с убывающим, недостающие коэффициенты заменяются нулями. Например, для системы, имеющей характеристическое уравнение 4-й степени, получим

. (2.5)

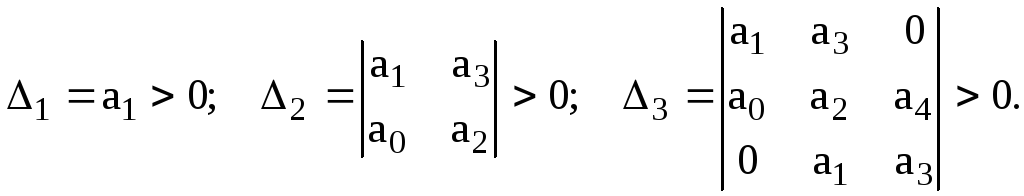
Поскольку , то при соблюдении необходимого условия устойчивости (положительность всех коэффициентов) достаточно чтобы положительными были диагональный минор. Очевидным является также утверждение, что при будет иметь место нулевой корень характеристического уравнения, т.е. система будет находиться на границе устойчивости. Если , а , то в характеристическом уравнении будут чисто мнимые корни, и она также будет на границе устойчивости. При этом все главные диагональные миноры до порядка должны быть положительными.

№25. Частотный критерий устойчивости Михайлова.

Если в характеристическом уравнении положить , то получим годограф Михайлова

(2.6)

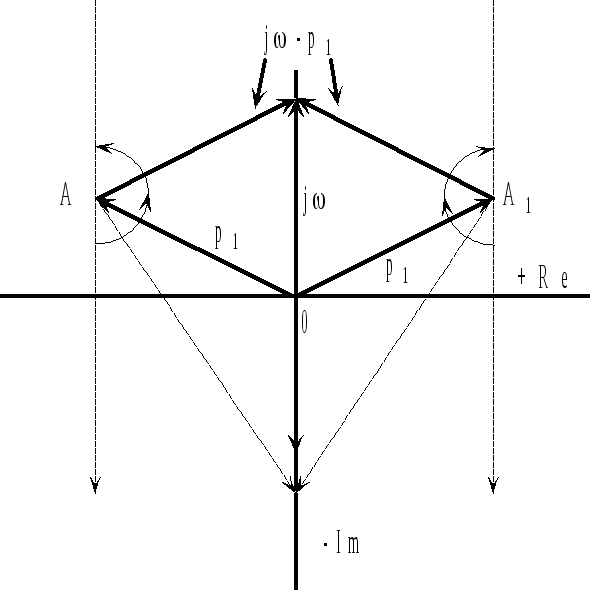
Найдем угол поворота элементарного вектора при изменении  от до (рисунок 2.1). При этом могут быть два случая: корень находится в левой полуплоскости комплексной плоскости, т.е. имеет отрицательную вещественную часть; корень находится в правой полуплоскости комплексной плоскости.

Если корень в левой полуплоскости, то при вектор направлен вниз. При увеличении вектор поворачивается против часовой стрелки ( в положительном направлении ) и при направлен вверх, т.е.

Если корень находится в правой полуплоскости, то вектор повернется аналогично предыдущему случаю только по часовой стрелке, т.е.

Вектор представляет произведение элементарных векторов (2.6), поэтому, если все корни характеристического уравнения (2.2) находятся в левой полуплоскости комплексной полуплоскости, т.е. САУ устойчива, то

(2.7)

где

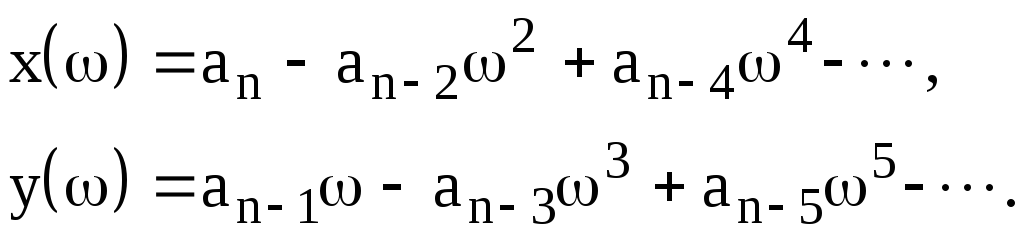
Вещественная часть равна есть частная функция, поэтому ветвь , построенная при изменении от до 0, будет симметрична ветви при изменении от 0 до . Поэтому нет смысла изменять от до достаточно построить при изменении от 0 до . При этом приращение аргумента будет в два раза меньше. Если САУ имеет характеристическое уравнение, корни которого находятся в левой полуплоскости, то

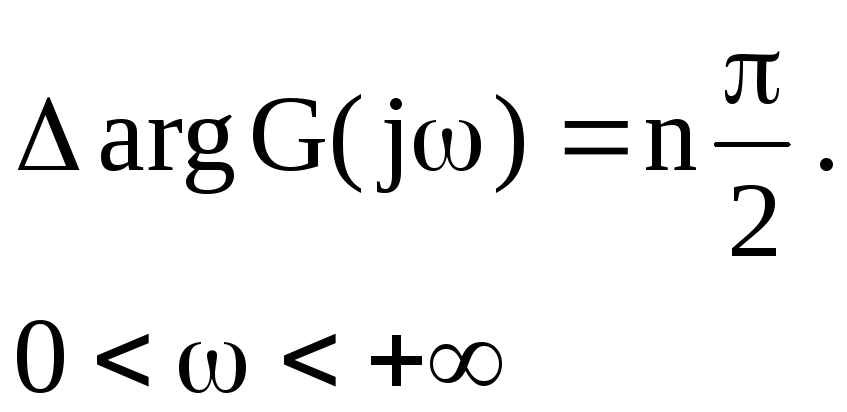
Поскольку необходимое условие требует положительности и наличия всех коэффициентов характеристического уравнения, то для устойчивой САУ .

САУ будет устойчива, если годограф Михайлова, начинаясь на положительной вещественной полуоси, последовательно проходит в положительном направлении (против часовой стрелки) "" квадрантов при изменении от 0 до ,

где - степень характеристического уравнения.

Годограф Михайлова для устойчивых САУ при изображены на рисунке 2.2. Если годограф Михайлова проходит через начало координат, то САУ находится на границе устойчивости. При этом, если он начинается с нуля, то это указывает на наличие нулевого корня, если годограф начинается на положительной вещественной полуоси, но затем проходит через начало координат, то это значит имеются мнимые корни в характеристическом уравнении.

Если годограф Михайлова непоследовательно проходит квадранты комплексной плоскости или проходит не "" квадрантов, то САУ неустойчива.

Пусть характеристическое уравнение n-й степени имеет m корней в правой полуплоскости. Тогда

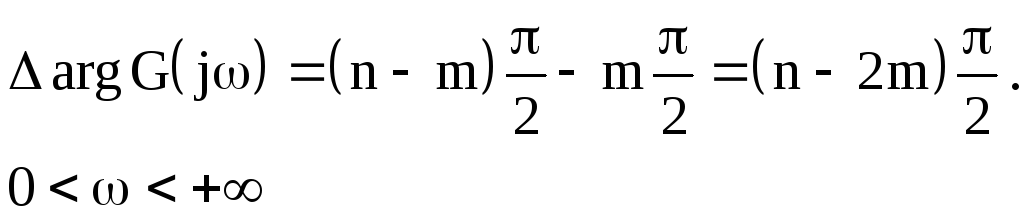
Итак, критерий устойчивости Михайлова позволяет не только анализировать устойчивость замкнутых и разомкнутых САУ, но и находить число неустойчивых корней

.

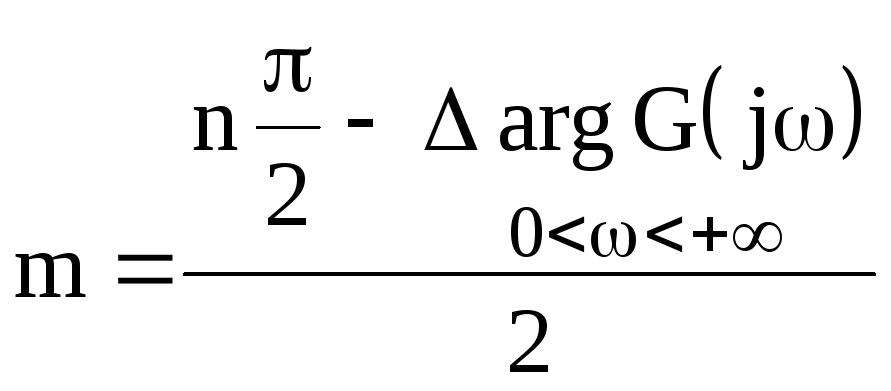Для устойчивой САУ очевидным является свойство чередуемости и вещественности корней и .

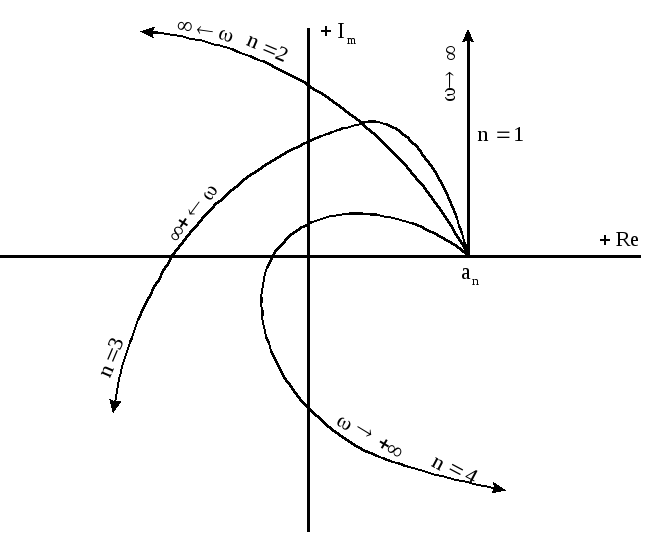
Рисунок 2.2 - Виды годографов Михайлова

№26. Частотный критерий устойчивости Найквитса – Михайлова.

С помощью критерия устойчивости Найквиста-Михайлова по стационарным свойствам разомкнутой САУ можно судить о нестационарных свойствах замкнутой.

Известно, что характеристическое уравнение замкнутой САУ, определяющее ее устойчивость, получается приравниванием нулю знаменателя передаточной функции замкнутой системы, т.е. .

Обозначим тогда (2.8)

Если в выражении (2.8) заменить на , то в числителе получим годограф Михайлова для замкнутой системы, а в знаменателе - для разомкнутой. При этом степень числителя и знаменателя будут одинаковы и, если замкнутая и разомкнутая системы устойчивы, то

.

На комплексной плоскости это обозначает, что вектор при изменении от 0 до не поворачивается вокруг точки , или что вектор не охватывает на комплексной плоскости точку при изменении от 0 до (рисунок 2.3).

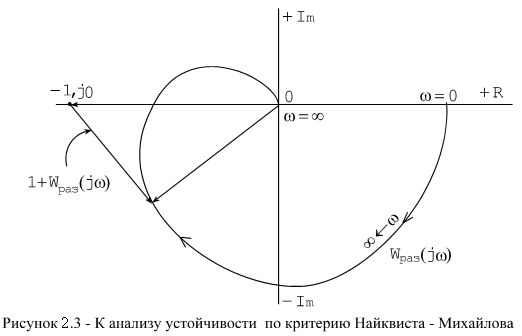
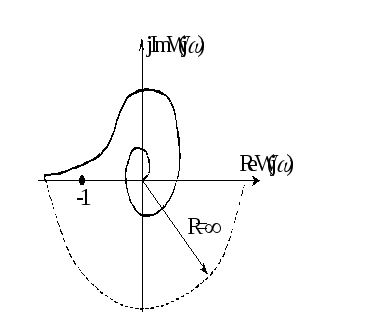
Таким образом, если разомкнутая САУ устойчива и ее АФХ не охватывает на комплексной плоскости точку с координатами , то замкнутая САУ будет устойчива.

Если разомкнутая САУ неустойчива и имеет неустойчивых корней, а замкнутая САУ устойчива, то

Таким образом, если разомкнутая САУ неустойчива и имеет неустойчивых корней, то для устойчивости САУ в замкнутом состоянии необходимо, чтобы АФХ разомкнутой системы охватывала в положительном направлении точку на комплексной плоскости с координатами раз.

Если разомкнутая САУ неустойчива, то число неустойчивых корней можно определить по критерию Михайлова.

В том случае, если разомкнутая САУ находиться на границе устойчивости благодаря наличию нулевых корней, передаточную функцию ее можно записать так:

где - кратность нулевого корня.

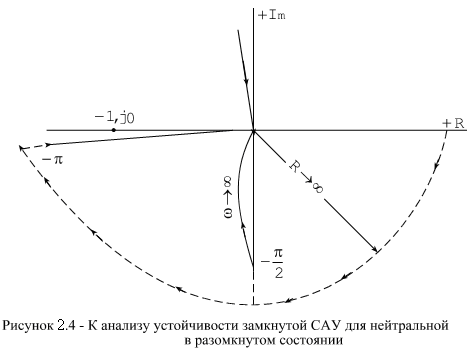
АФХ разомкнутой системы стремиться к началу координат при увеличении  по одной из осей координат комплексной плоскости:

при т.е. АФХ перемещается по отрицательной мнимой оси;

при т.е. АФХ перемещается по отрицательной вещественной оси;

при т.е. АФХ перемещается по положительной мнимой оси.

Для анализа устойчивости таких систем справедлив критерий устойчивости Найквиста-Михайлова, если их АФХ дополнить частью окружности бесконечного радиуса, которая

начинается на положительной вещественной полуоси, как это показано на рисунке 2.4.

№27 Устойчивость САУ с запаздыванием

Если САУ имеет чистое запаздывание, то ее устойчивость можно определить только по критерию Найквиста-Михайлова, поскольку характеристическое уравнение будет иметь бесконечное множество корней из-за наличия сомножителя , делающего его трансцендентным.

Систему с чистым запаздыванием можно рассматривать как предельную систему без запаздывания и звена чистого запаздывания, включенного последовательно:

(2.11)

Из выражения (2.11) следует, что наличие чистого запаздывания не изменяет амплитудно-частотную характеристику, модуль АФХ остается прежним, но изменяется фаза векторов - каждый из них поворачивается по часовой стрелке на угол . Поскольку значения модуля АФХ, как правило, больше при малых частотах, то наличие чистого запаздывания приводит к «разбуханию» АФХ, и она может охватить на комплексной плоскости точку с координатами .

Для определения критического значения , при котором САУ еще устойчива, проводят из начала координат комплексной плоскости единичным радиусом окружность. Точка пересечения ее с АФХ характеризует частоту , при которой Зная , можно найти 

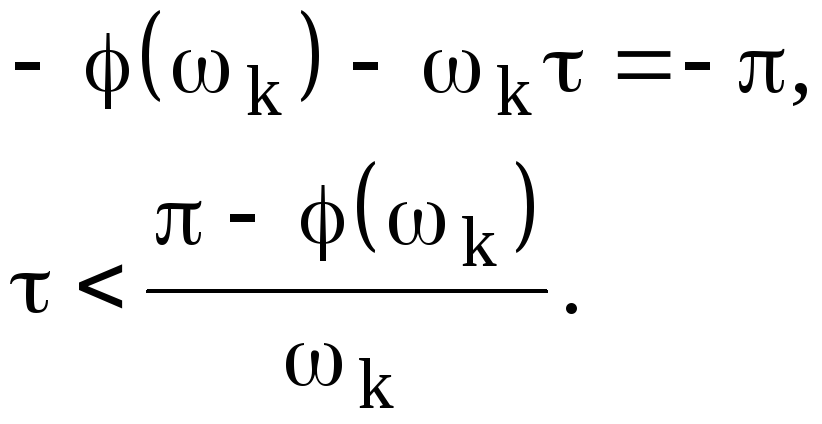
Построив АФХ разомкнутой САУ, можно найти запас устойчивости замкнутой САУ по модулю и по фазе (рисунок 2.5,б). Запас устойчивости по фазе есть угол . Запас устойчивости по модулю иногда определяют по расстоянию от точки пересечения АФХ с отрицательной вещественной осью до минус единицы, иногда как величину , где - расстояние от точки пересечения АФХ с отрицательной вещественной осью до начала координат.

№ 28 Структурная неустойчивость САУ.

Это такое свойство замкнутой системы, при наличии которого она не может быть сделана устойчивой ни при каких изменениях параметров.

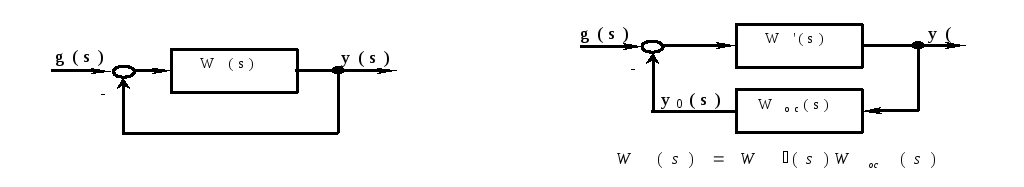
Пусть 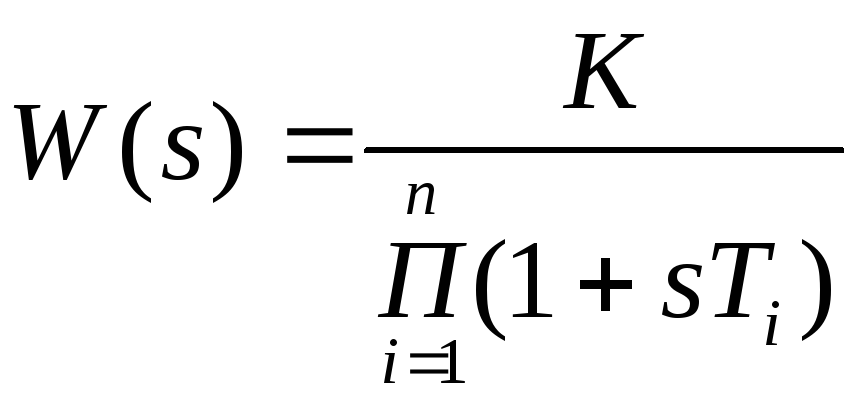. Годограф Найквиста для данной системы изображен на Рис.А. Устойчивость этой системы определяется значениями параметров и . Рассматриваемая система является структурно устойчивой.

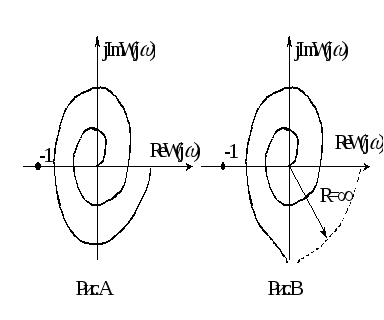
Пусть 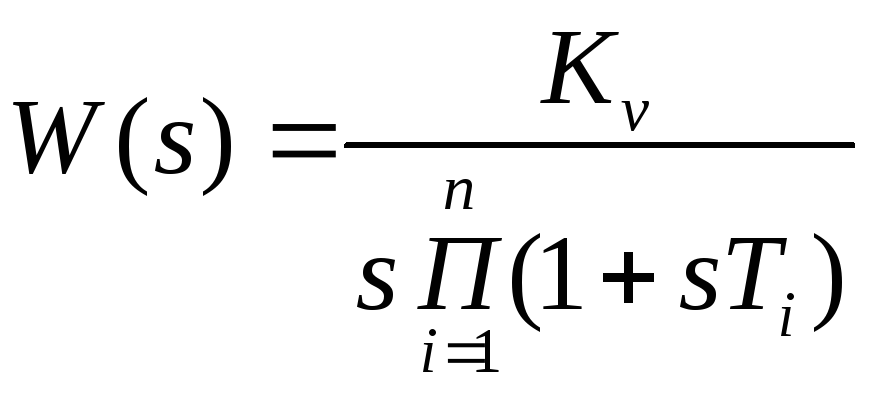. (Рис.В). Устойчивость также зависит от параметров и . Система структурно устойчива.

Пусть 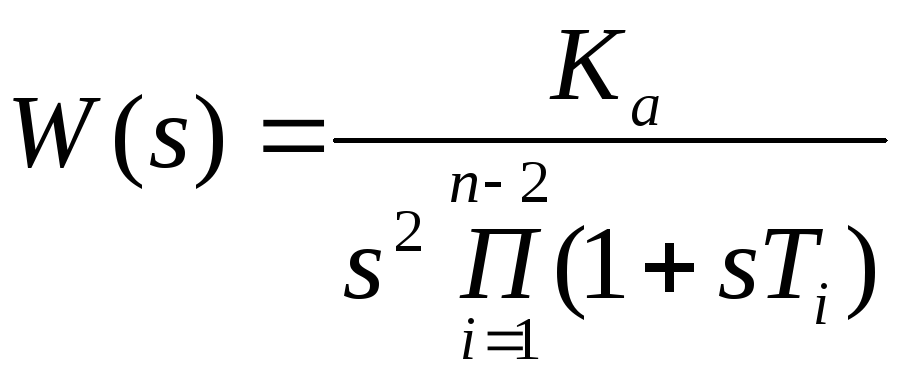. В любом случае (при любых значениях параметров) система будет неустойчива. То есть система является структурно неустойчивой.

В частном случае передаточная функция имеет вид . При этом соответствующее характеристическое уравнение замкнутой системы: . Нарушен принцип перемежаемости корней и полюсов. Система неустойчива. Структурно неустойчива.

Система с передаточной функцией - структурно неустойчива, так как для замкнутой системы, при этом коэффициенты,,,, - все положительны, но из условияследует, что, откуда, или. То есть система неустойчива.

Система также структурно устойчива. Здесь звено- квазиапериодическое (статически неустойчиво). Характеристическое уравнение замкнутой системы. Откуда можно получить два граничных условия:и.

Для одноконтурных систем имеют место условия (Мейеров М.В.):

Пусть одноконтурная система состоит из:

- интегрирующих звеньев,

- неустойчивых звеньев,

- консервативных звеньев. Тогда при отсутствии в системе дифференцирующих звеньев она будет структурно устойчива в том случае, если

В случае многоконтурных систем соотношения Мейерова необходимо применять к каждому контуру, входящему в систему.

№ 29 Граница устойчивости и область устойчивости в плоскости одном и двух параметров

Для выделения области параметров, обеспечивающих устойчивую работу САУ, используются критерии устойчивости. Рассмотрим приме­нение каждого из них для выделения области устойчивости по одному и двум параметрам.

Критерий устойчивости Гурвица.

Пусть САУ имеет один параметр настройки . Для выделения об­ласти значений , обеспечивающих устойчивость САУ запишем все условия устойчивости - положительность всех главных диагональных миноров до «» при . В частном случае может входить и в . Равенство нулю миноров соответствует границе устойчивости.

Если построить зависимости , , то значение параметра , удовлетворяющие условию устойчивости, будет лежать на оси абсцисс в той области зна­чений , для которых миноры положительны.

Если САУ имеет два параметра настройки и , то приравняв нулю получим уравнение границы устойчивости в плоскости двух пара­метров. Задаваясь значениями одной из них, по каждому уравнению можно найти значение другого и построить линии границы устойчивости. При этом плоскость параметров и будет разделена на области. Для определения области, удовлетворяющей условию устойчивости, необходимо из каждой области взять одну точку и проверить на устойчивость.

САУ находится на границе устойчивости, если характеристиче­ское уравнение имеет нулевые или мнимые корни.

Критерий Найквиста - Михайлова.

Возможны два варианта: и принадлежат одному звену; и принадлежат различным звеньям.

В первом случае АФХ разомкнутой системы представляют в таком виде:

.

Граница устойчивости определяется соотношениями:

; .

В нашем случае ;

.

Отсюда

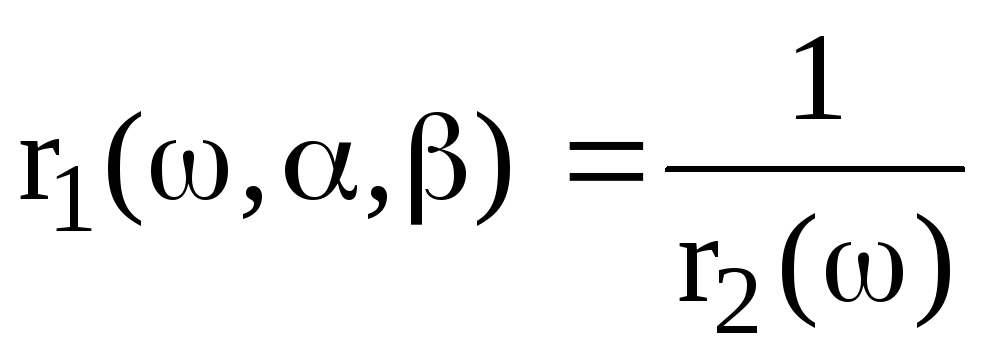; . (2.16)

Задаваясь , находят и , и . Решая совместно два уравнения с двумя неизвестными, находят точку на кривой границы устойчивости. Линию строят при изменении от до . Определение области устойчивости производится путем проверки одной точки каждой области.

Если и принадлежат различным звеньям, то получают две передаточные функции, в одну из которых входит , в другую .

Уравнения границы устойчивости в этом случае такие:

; . (2.17)

Подставляя конкретные значения , решают совместно систему двух уравнений, в результате которого получают значения и для выбранной частоты, соответствующие одной точке на линии границы устойчивости. Если система уравнений не решается аналитически, используется графоаналитический метод.

№ 30 Анализ качества САУ

Качество регулирования определяется отклонением регулируемой величины от желаемого закона ее изменения в установившемся и переходном режимах. Статические показатели качества характеризуются статической погрешностью. Динамические показатели качества характеризуются временем регулирования, перерегулированием, числом перерегулирований, формой кривой переходного процесса (апериодический, колебательный).

Время регулирования определяется как время от начала переходного процесса до момента, когда выполняется условие:

, (2.18)

где - величина, определяемая требуемой погрешностью работы САУ, обычно .

Перерегулированием называют отношение максимального отклонения регулируемой величины от установившегося значения к величине установившегося значения

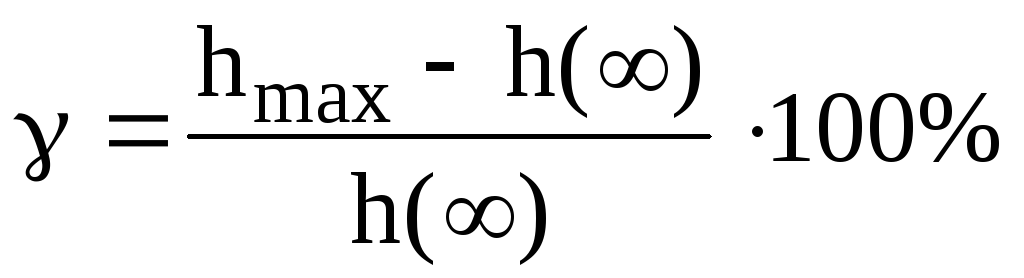. (2.19)

Число перерегулирований определяется по числу максимумов за время регулирования, когда

. (2.20)

Апериодическим называется переходный процесс, при котором регулируемая величина приближается к установившемуся значению без колебаний. Иногда под апериодическим переходным процессом понимают процесс, составляющими которого являются экспоненты, хотя сумма экспонент с различными начальными значениями и постоянными времени может дать несколько колебаний (процесс при отрицательных вещественных корнях характеристического уравнения).

Существуют прямые и косвенные методы оценки качества САУ. Прямые методы предполагают анализ САУ непосредственно путем построения переходного процесса. Косвенные методы позволяют ориентировочно судить о переходном процессе без его построения. К ним относятся: определение степени устойчивости, апериодичности, интегральные критерии качества. Рассмотрим их подробнее.

№ 31 Критерии апериодичности переходного процесса

Критерий А. М. Каца базируется на вещественности корней характеристического уравнения. Корни характеристического уравнения будут вещественными, если полином удовлетворяет условию устойчивости, где -получается из характеристического уравнения заменой на в производной по от .

Это утверждение легко доказать.

Если в подставить , то получим .

Если удовлетворяет условию устойчивости, то вещественная и мнимая части , т.е. и имеют вещественные перемежающиеся корни. Но корни вещественны относительно , что равносильно вещественности корней относительно . Поскольку система устойчива, то они отрицательны.

Построив для границу устойчивости, мы тем самым строим границу апериодичности для . Степень в два раза выше степени , поэтому условия апериодичности будут сложнее условий устойчивости.

Критерий Л.Эйлера (1765 г.) позволяет получить условие апериодичности переходного процесса по коэффициентам характеристического уравнения. При этом корни характеристического уравнения могут быть комплексно-сопряженными с отрицательными вещественными частями.

Если характеристическое уравнение записать в форме

,

то для апериодичности переходного процесса необходимо, чтобы для любых смежных коэффициентов выполнялось условие:

, (2.21)

где - степень характеристического уравнения; - индекс проверяемого коэффициента, .

Невыполнение хотя бы одного из неравенств следует считать признаком отсутствия апериодической устойчивости.

Критерий Штурма. Предложен в Парижской Академии в 1826 г. в виде теоремы, из которой вытекает условие апериодичности.

Все корни характеристического уравнения будут отрицательными, если положительны все коэффициенты числом +1 при старших членах ряда Штурма, полученного из этого уравнения, где - его степень.

Ряд Штурма образуется следующим образом:

где - характеристическое уравнение САУ; - производная от по ; - остаток от деления на , взятый с обратным знаком.

Остальные члены ряда получаются таким же образом.

;;.... (2.22)

При последовательном делении полиномов для образования ряда Штурма можно умножать или делить на какое-либо постоянное положительное число, не зависящее от . Число членов ряда Штурма должно быть +1. Члены ряда должны иметь степень , убывающую на единицу, и последний член должен состоять только из коэффициентов характеристического уравнения.

Недостаток рассмотренных критериев состоит в том, что они не учитывают свойств возмущений, действующих на САУ (не учитывают правую часть дифференциального уравнения).

Для анализа качества систем управления, описываемых дифференциальными уравнениями третьего порядка, И. А. Вышнеградский (1831-1895 гг.) разработал диаграмму, по которой в плоскости двух параметров Вышнеградского можно найти область устойчивости, апе риодичности, отсутствия перерегулирования, области равного абсолютного затухания, относительной степени затухания. Однако в связи с частным случаем решенной задачи исследования по данному вопросу не приводятся и могут быть найдены практически в любом учебнике по теории автоматического управления.

№ 32 Введение производной в закон регулирования

Передаточная функция разомкнутой нескорректированной САУ . При анализе устойчивости САУ по критерию Найквиста - Михайлова строится АФХ разомкнутой системы. После введения корректирующего звена результирующая передаточная функция разомкнутой системы будет. При этом ее АФХ также изменится. Обозначим ее:

. (8.1)

Из выражения (8.1) видно, что наличие производной приводит к деформации исходной АФХ за счет добавления к каждому вектору дополнительного вектора, направленного перпендикулярно исходному в положительном направлении, рисунок 8.2. (против хода часовой стрелки).

На рисунке 8.2 деформированная АФХ пересекает отрицательную вещественную ось правее исходной, т.е. введение производной может увеличить запас устойчивости по модулю. Однако это не всегда так. В зависимости от формы и выбора величиныналичие производной может как повысить, так и понизить запас устойчивости по модулю (удалить или приблизить АФХ к критической точке на комплексной плоскости).

Введение производной повышает быстродействие САУ.

Действительно, пусть . Тогда, подобрав,

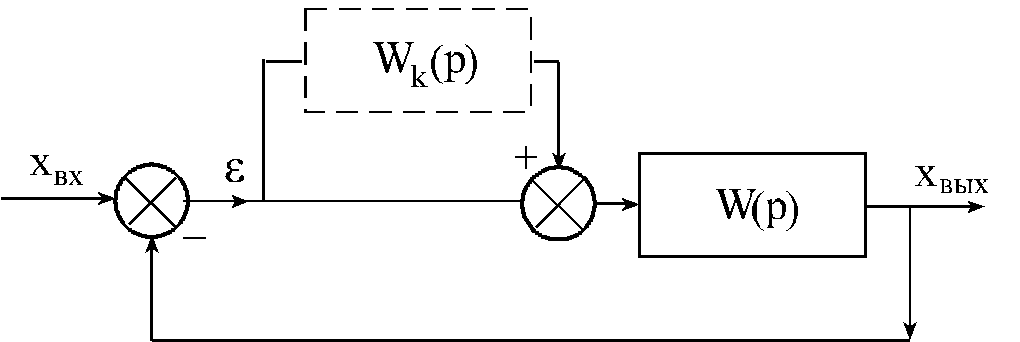
Рисунок 8.1 - Структурная схема инвариантной САУ

Рисунок 8.2 - АФХ исходной САУ и при введении производной

получим систему, на выходе мгновенно воспроизводящую входной сигнал. Передаточная функция замкнутой системы:

.

В итоге система превращается в усилительное звено, мгновенно воспроизводящее во времени и по форме входной сигнал.

Для системы с после коррекции получаем. Характеристическое уравнение замкнутой САУ:. Условие устойчивости по Гурвицу.

Предельное значение , при котором исходная система приходит к границе устойчивости:. Для скорректированной САУ, т.е.. Это позволяет увеличить коэффициент усиления разомкнутой системы и таким образом, снизить статическую погрешность САУ.

№ 33 Введение интеграла в закон регулирования

Пусть на рисунке 8.1 в качестве корректирующего звена используется интегрирующее с. Тогда передаточная функция разомкнутой скорректированной системы

.

Введение корректирующего интегрирующего звена деформирует АФХ ра­зомкнутой системы:

К каждому вектору исходной АФХ добавляется вектор

, который направлен вод углом 90° по часовой стрелке по отношению к основному. Кроме того, величина его тем больше, чем меньше . Как видно из рисунка 8.3, наличие интегрирующего зве­на в законе управления всегда деформирует АФХ исходной системы в сторону ее разбухания.

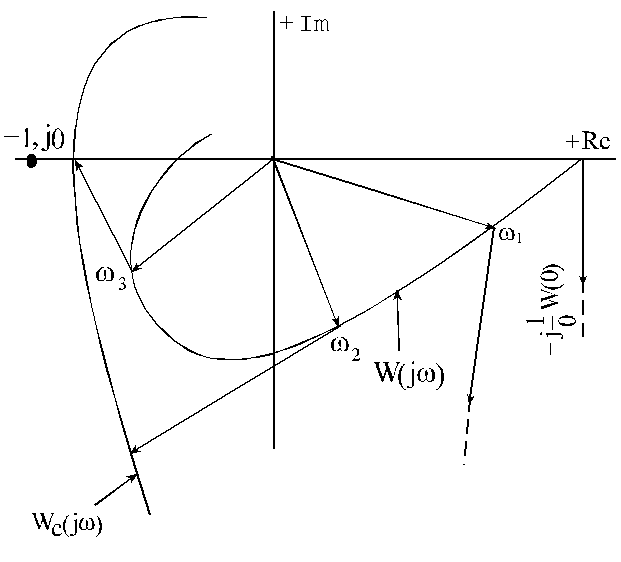
Рисунок 8.3 - АФХ исходной САУ при введении интеграла

При этом запас устойчивости САУ по модулю и фазе уменьшается.

Для выяснения влияния интегрирующей составляющей на статичес­кую погрешность обратимся опять к рисунку 8.1. Здесь статическая погрешность . Передаточная функция замкнутой САУ междуи входным сигналом- для не скорректированной системы.

Пусть , тогда

(8.2)

Для скорректированной системы

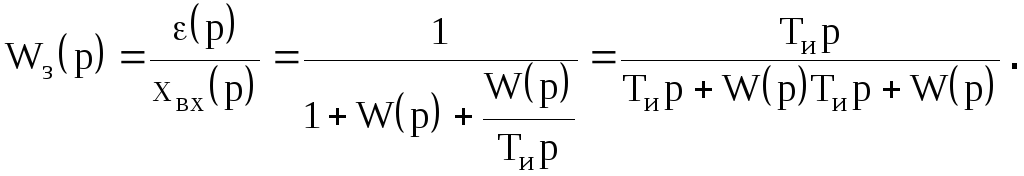
Предположив, как и в первом случае , получим

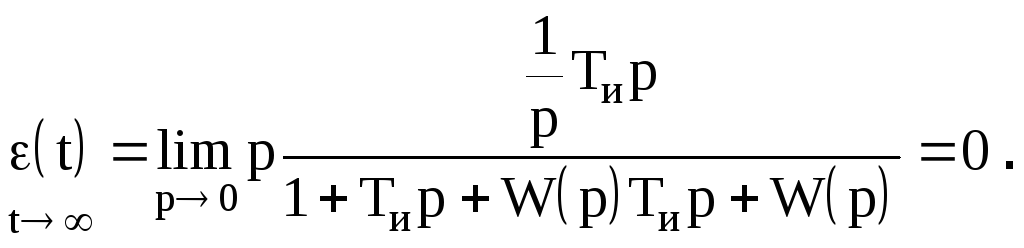(8.3)

Введение интегральной составляющей исключает статическую ошибку регулирования.

Введение звеньев в цепь прохождения основного сигнала называ­ется последовательной коррекцией. Она проста, но чувствительна к помехам и требует дополнительных усилителей. Если корректирующее звено вводится в цепь обратной связи, то коррекция называется параллель­ной. Она уменьшает нестабильность и нелинейность характеристик отдельных элементов.

Питание цепей обратной связи осуществляется с выхода последую­щих элементов, имеющих большую мощность и не вызывает затруднений. Высокочастотная составляющая фильтруется звеньями прямой связи, поэтому параллельная коррекция нечувствительна к помехам. Однако она требует применения громоздких устройств (трансформаторы, тахогенераторы и т.д.).

№ 34 Создание инвариантных САУ

В настоящее время существует три направления создания инвари­антных САУ:

1. Системы с одной регулируемой величиной, работающие по отк­лонению. В таких системах условие абсолютной инвариантности достигается при коэффициенте усиления разомкнутой САУ равном бесконеч­ности.

2. Создание комбинированных систем.

3.Использование принципа двухканальности Б.Н. Петрова в многосвязных системах.

САУ называется инвариантной по отношению к возмущающему воз­действию, если после завершения переходного процесса, определяе­мого начальными условиями, регулируемая величина и ошибка систе­мы не зависят от этого воздействия.

САУ называется инвариантной по отношению к задающему воздейст­вию, если после завершения переходного процесса, определяемого начальными условиями, ее ошибка не зависит от этого воздействия.

При нулевых начальных условиях

где - передаточная функция САУ,

В соответствии с правилами определения оригинала функции при отсутствии кратных корней

(8.4)

где - корни полинома;

- корни полинома .

Вынужденная составляющая будет тождественно равна нулю, если:

- входное воздействие отсутствует;

- условие абсолютной инвариантности (равенство нулю пе­редаточной Функции замкнутой САУ по отношению к возмущающему воз­действию).

Корни совпадают с корнями ии сомножители, соответст­вующие им, можно сократить. Этот случай соответствует частичной инвариантности, когда САУ будет инвариантна только к определенному виду возмущений.

Под частичной инвариантностью (до ) понимается не тождественное равенство нулю вынужденной составляющей, а приближенное, мерой выполнения которого является некоторая величина.

№ 35 Создание комбинированных САУ

Основным методом, используемым при создании инвариантных систем, является применение комбинированного управления, при котором управляющее воздействие реализуется не только по отклонению регулируемой величины, но и по возмущению, для этого измеряется ос­новное возмущающее воздействием и сигнал через корректирующее зве­но вводится в САУ.

При этом реализуется принцип двухканальности и не возникает противоречия между устойчивостью и инвариантностью, как это имеет место в одноконтурных системах, реализующих условие инвариантнос­ти за счет повышения коэффициента усиления системы.

Условия реализации абсолютной инвариантности легко проследить на примерах (рисунок 8.4,8.5).

Для системы (рисунок 8.4)

Отсюда (8.5)

Для системы (8.5):

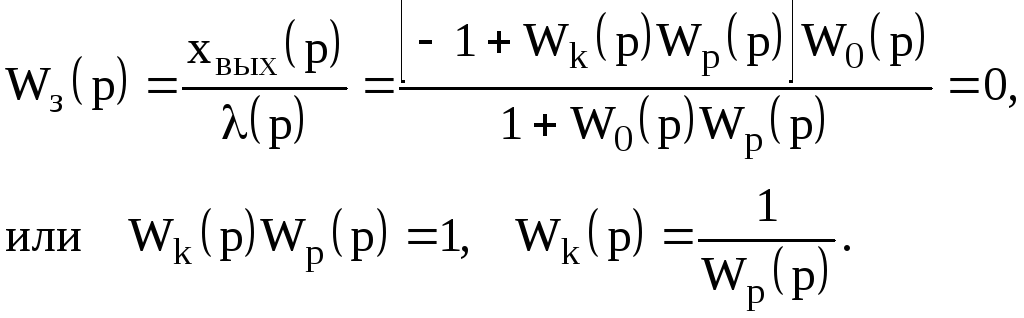(8.6)

Введение дополнительных воздействий не изменяет характеристического уравнения замкнутой САУ, поскольку корректирующие звенья не входят в замкнутый контур прохождения сигнала. При этом не бу­дет нарушаться не только устойчивость САУ, но и сохраняться оценки качества переходного процесса, базирующиеся на использовании кор­ней характеристического уравнения.

Поскольку для физической реализации передаточной функции 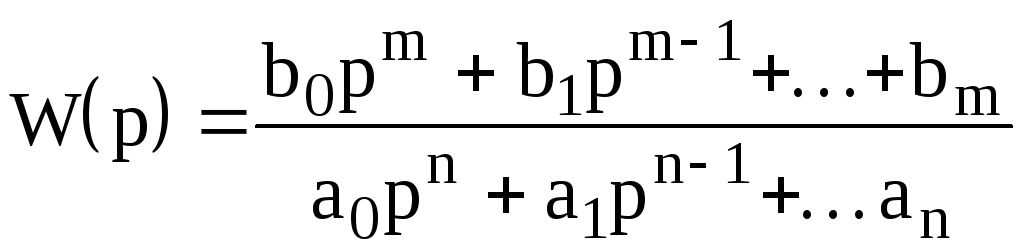необходимо, чтобы , то при реализации условия абсолютной инвариантности сталкиваются с затруднениями реализации производных. Например, если

Это звено физически реализуемо, . Это реальное дифференцирующее звено.

При

Если регулятор обладает астатизмом -го порядка, тодолжно реализовать производную-го и выше порядков и не иметь производных допорядка, что физически невозможно реа­лизовать.

В этом случае реализуется частичная инвариантность за счет замены идеальных дифференцирующих звеньев реальными.

Рисунок 8.4 - Реализация инвариантности по заданию САУ

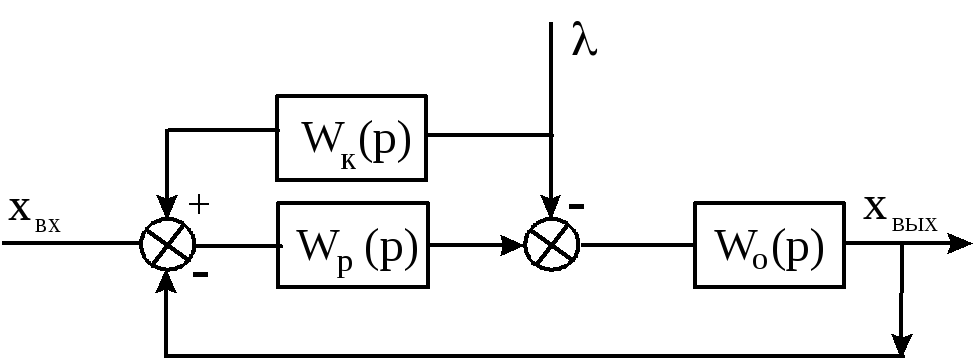
Рисунок 8.5 - Реализация инвариантности по возмущению САУ

Можно реализовать инвариантность по нескольким возмущениям, но это практически сложно.

Для САУ, описываемых дифференциальными уравнениями 1-го и 2-го порядка, когда необходимое условие устойчивости (положи­тельность коэффициентов характеристического уравнения) является и достаточным, можно корректирующие звенья не устанавливать, а увеличивать коэффициент усиления разомкнутой САУ. При этом (рисунок 8.4):

Коэффициент усиления разомкнутой САУ равен . Для того, чтобы САУ была инвариантна к задающему воздей­ствию, необходимо, чтобы

. Это отношение будет стремиться к единице при . При этом САУ будет инвариантна и к возмущающему воздействию (рисунок 8.5).

Если

36. Инвариантность по задающему воздействию

В настоящее время существует три направления создания инвариантных САУ:

1. Системы с одной регулируемой величиной, работающие по отклонению. В таких системах условие абсолютной инвариантности достигается при коэффициенте усиления разомкнутой САУ равном бесконечности.

2. Создание комбинированных систем.

3. Использование принципа двухканальности Б.Н. Петрова в многосвязных системах.

САУ называется инвариантной по отношению к задающему воздействию, если после завершения переходного процесса, определяемого начальными условиями, ее ошибка не зависит от этого воздействия.

САУ инвариантна к задающему воздействию, если ее передаточная функция по отношению к нему равна единице W(p)=1.

37. Инвариантность по возмущающему воздействию

САУ называется инвариантной по отношению к возмущающему воздействию, если после завершения переходного процесса, определяе­мого начальными условиями, регулируемая величина и ошибка системы не зависят от этого воздействия.

САУ инвариантна к возмущающему воздействию, если ее передаточная функция по отношению к нему равна нулю W(p)=0.

Возмущающее воздействие – это такое воздействие, которое стремится нарушить требуемую функциональную связь между переменными, характеризующими ее состояние.

38. Основные типы нелинейностей

Нелинейной системой автоматического управления называется такая система, которая содержит хотя бы одно звено, описываемое нелинейным уравнением.

Нелинейности бывают:

• релейного типа

• динамические (описываются нелинейными дифференциальными зависимостями);

• переменной структуры (эта нелинейность связана с изменением значения переменной х, например: система, состоящая из линейных звеньев, создает нелинейное устройство, реализующее определенную функцию переключения Ф (фи))

• логического типа (элемент, имеющий несколько входов выдает ступенчатый сигнал. В зависимости от определенных логических комбинаций входных величин.)

• релейные автоматические системы

39. Нелинейности релейного типа.

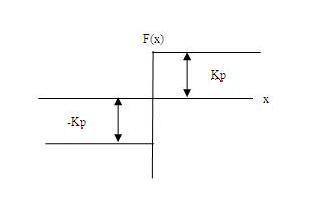
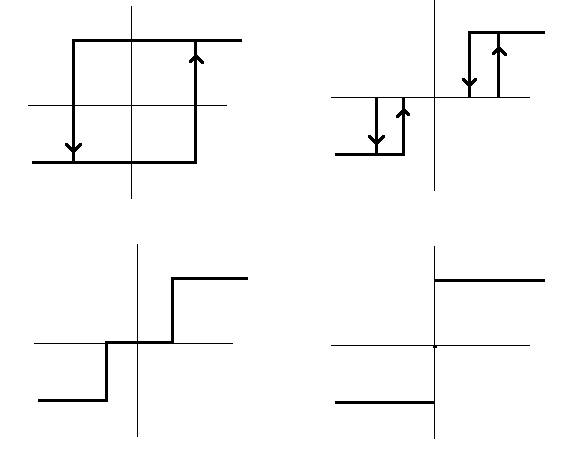
Характеристика релейного элемента без среднего положения (2х-розиционный).

40. Релейные автоматические системы.

Это наиболее простой класс нелинейных систем, т.к. благодаря специфике релейного элемента, создающего воздействие на релейную часть системы в виде прямоугольных импульсов одинаковой высоты. Исследования сводятся к исследованию линейной части, подверженной этим импульсам.

Управляющее воздействие приложенное к линейной части системы можно представить в виде суммы воздействий простейшего вида, а реакцию линейной части найти по принципу суперпозиции на сумму реакций на каждое из них.

41. Построение переходных процессов в релейных системах.

Главная особенность релейных систем что они не подчиняются принципу наложения, а форма и показатели переходного процесса зависят от величины и формы внешнего воздействия.

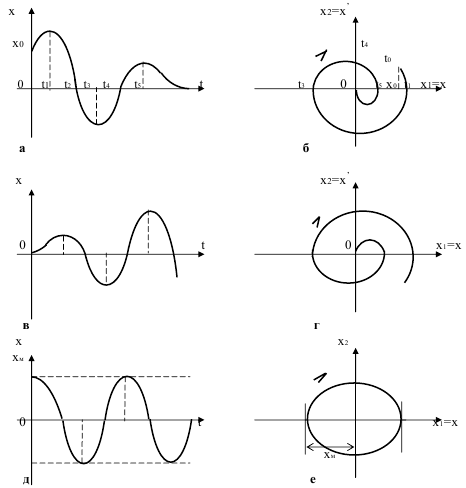
42. Устойчивость нелинейных систем.

Самые важные для анализа нелинейных систем свойства фазовых траекторий заключаются в следующем:

• Неустойчивому процессу соответствует фазовая траектория, удаляющаяся от начала координат.

• Периодическому процессу соответствует замкнутая фазовая траектория, называемая предельным циклом.

Устойчивость нелинейной системы оценивают по 3 признакам:

– устойчивость в малом – это устойчивость системы при бесконечно малых отклонениях от исходного режима. При чуть больших отклонениях система становится неустойчивой.

– система устойчива в большом, если система устойчива при бесконечно больших отклонениях, которые возможны в данной системе. При малых система может быть неустойчива.

– система устойчива в целом, если система устойчива при любых воздействиях.