43. Устойчивость релейных систем.

Релейная автоматическая система устойчива, если для всякого заданного числа Е>0 можно найти такое число N(E)>0 что для всех изчезающих воздействий f(t), таких что , входная величина релейного элемента x(t) удовлетворит неравенству для всех t>t0.

Если релейная автоматическая система устойчива лишь при достаточно малых значениях, то имеет место устойчивость в малом. Если же релейная система устойчива при любых конечных значениях, то имеет место устойчивость в большом. Если релейная система устойчива при любых N, то имеет место устойчивость в целом.

44. Вынужденные колебания в релейных системах.

Внешнее периодическое воздействие навязывает системе свою частоту и подавляет автоколебания, возможные в системе. В этом случае система автоматически синхронизируется частотой внешнего воздействия. В ней имеет место вынужденные колебания, частота которых равна частоте внешнего воздействия.

45. Линеаризация релейных систем.

Подача на вход релейного элемента дополнительного высокочастотного периодического воздействия наряду с медленно изменяющейся по сравнению с ним входной величиной (управляющим сигналом) приводит, по крайней мере при малых изменениях, к линеаризации релейного элемента, т.е. к тому что среднее значение выходной величины его становится пропорциональной величине х(т). При этих условиях релейный элемент эквивалентен линейному усилителю. Характерная особенность такого усилителя является зависимость коэффициента усиления от амплитуды внешнего воздействия. Увеличение последней уменьшает коэффициент усиления.

46. Основные определения теории оптимальных систем.

Опр.1. Задачи управления – формализация и реализация для перевода его в нужное состояние.

Опр.2. Объект – часть окружающей среды, выделенная так, что выполняется 2 условия:

на объект можно воздействовать;

воздействие может изменить состояние объекта в нужном направлении.

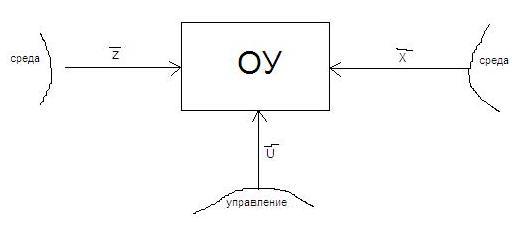
Опр.3. Алгоритм управления – совокупность правил, методов и способов, позволяющих синтезировать оптимальное управляющее воздействие на объект в реальных условиях.

Опр.4. Управляющее устройство реализует алгоритм управления.

Опр.5. Система управления – совокупность объектов управления и управляющего воздействия.

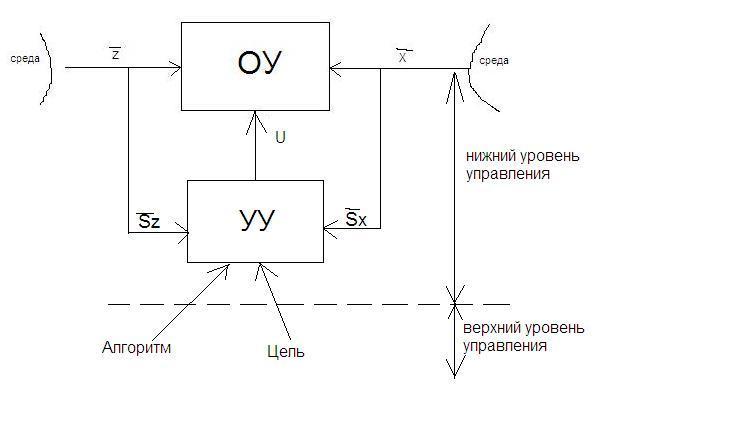
Опр.6. Критерий оптимальности – количественная оценка качества функционирования объекта.

Опр.7. Целевая функция (функция качества) – формализованное выражения критерия оптимальности.

Опр.8. Оптимальные системы – системы управления, обеспечивающие экстремальное значение критерия при заданных условиях.

Опр.9. Оптимальное управление – соответствующее управление.

47. Этапы решения задач оптимизации.

   Постановка задачи на оптимизацию и ее решение включает в себя ряд этапов:

•   выбор и обоснование цели оптимизации; •   согласование цели с имеющимися возможностями, т.е. учет ограничений; •   реализация способа достижения цели (экспериментального значения критерия качества ) при учете ограничений.

      Выбор и обоснование цели оптимизации предусматривают определение критериев качества (целевых функций), которые наиболее полно отражали бы цели оптимизации. Этот этап является одним из основных, так как от правильности выбора критерия качества зависит решение задачи в целом.       Второй этап решения задачи связан с определением ограничений, которые должны учитываться в процессе оптимизации. Смысл этого этапа заключается в том, что часто качество системы характеризуется не одним, а группой показателей качества, поэтому если система оптимизируется по одному показателю качества, то другие могут достичь такой величины. Следовательно, если выбран какой-либо параметр системы как критерий качества, то на другие показатели качества и варьируемые параметры накладываются ограничения.       При реализации третьего этапа применяется тот или иной метод оптимизации, обеспечивающий решение поставленной задачи - достижение экстремального значения критерия качества при учете ограничений