5.1.1. Резонанс напряжений

Резонансный режим в цепи с последовательным соединением участков, содержащих реактивные элементы различного характера, носит название резонанс напряжений. Признаком резонанса напряжения является равенство реактивных составляющих напряжений на последовательно включенных реактивных элементах различного характера.

; ;

; ; ;

; .

Условие резонанса:

;

.

Признаки резонанса:

;

;;

;;;

;

.

–добротность последовательного контура. Показывает, во сколько раз при резонансе напряжения на реактивных элементах контура превышает напряжение на входе цепи.

,

где - собственная (резонансная) частота контура.

Сопротивление индуктивного и емкостного элемента при резонансе называется характеристическим (волновым) сопротивлением последовательного RLC контура:

[Ом].

Тогда .

Величина обратная добротности – затухание контура:

.

Резонансные кривые – зависимости действующих и амплитудных значений напряжений и токов от частоты или параметров цепи: при U = const.

Полоса пропускания контура – диапазон частот  = _в - _н, на границах которого справедливо условие:

,

где _b, _h – верхняя и нижняя границы полосы пропускания.

Очевидно, чем больше добротность контура, тем острее резонансная кривая, тем уже полоса пропускания, тем лучше избирательность контура, то есть способность пропустить сигнал одной частоты и не пропускать остальное.

Можно показать, что

.

Относительная расстройка частоты– это отношение полосы пропускания к резонансной. Относительная расстройка частоты равна затуханию контура:

.

Частотные характеристики – зависимости от частоты параметров цепи – :

; .

Частотные характеристики можно получить расчетным или опытным путем. При снятии ЧХ опытным путем на вход двухполюсника подают напряжение, частоту которого изменяют в широких пределах и по результатам измерений рассчитывают Z_вx, R_вx, X_вx. Для несложных схем частотные характеристики можно получить из простых физических соображений:

если , то

Двухполюсник, составленный только из реактивных элементов – реактивный двухполюсник.

5.1.2. Резонанс токов

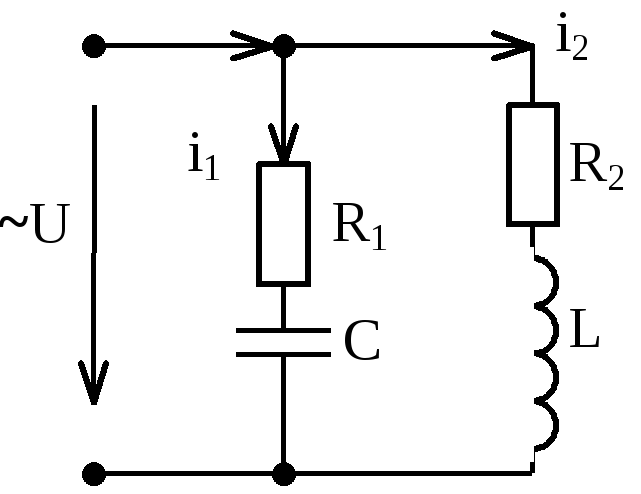
Резонансный режим с параллельным соединением таких участков называется резонансом токов. Характерным признаком резонанса токов является равенство реактивных составляющих токов в параллельных ветвях, содержащих реактивные элементы различного характера.

;

;

;

;

;

;

.

Условие резонанса:

; ; ;

.

В частности:

; ;

.

Признаки резонанса:

;

;

.

Резонансные кривыеI():

–добротностьпараллельного контура;

–характеристическая проводимость параллельного RLC контура.

Частотные характеристики:

Применение

По виду частотной характеристики можно определить какой тип резонанса и при какой частоте возникает в двухполюснике.

Точки, в которых частотная характеристика x() пересекает ось абсцисс (B() претерпевает разрыв от -до +) дают значение₀, при которых в цепи возникает резонанс напряжений.Точки, в которых кривая x() претерпевает разрыв от + до - (B()пересекает ось абсцисс), соответствует режимам резонанса тока.

24