11.2 Дифференциальные уравнения движения материальной точки.

Рассмотрим движения мат. точки по отношению к инерциальной с-ме отсчета, под действием системы сил

.- свободная мат точка

- несвободная мат точка.

В координатах на оси естеств 3-х гранника

Диф Ур-е мат точки на оси естеств 3-х гранника

тангенциальное

нормальное

В полярных корд.

=12=

Теорема об изменении момента кол-ва движения системы. Закон сохранения момента кол-ва движения системы.

- кинетический момент системы

Для твердого тела,если его рассматривать как систему:

Производная по времени от кинетического момента системы равна моменту всех внешних сил системы относительно той же оси.

Следствие(Закон сохранения):

если,то

если,то и т. п.

=15=

Работа силы тяжести:

Работа упругой силы:

Работа силы приложенной к телу , имеющему оси вращения:

=16=.

Механическая система. Масса, центр масс системы. Внешние и внутренние силы системы. Момент инерции твёрдого тела относительно центра, оси, плоскости.

Механическая система – это совокупность конечного и бесконечного числа материальных точек, связанных между собой таким образом, что положение и движение одной из точек системы зависит от положения и движения всех остальных точек.

Силы, действующие на точки системы делятся на:1. внутренние – это силы с которыми взаимодействуют точки системы между собой. 2. внешние – силы, действующие на точки механической системы со стороны других материальных объектов, не входящих в первоначальную систему. Для идеальных систем сумма всех внутренних сил и сумма их моментов относительно их точек =0.

Масса системы – арифметическая сумма масс всех точек системы.

Центр масс системы – одна из характеристик распределения масс – точка в которой сосредоточена масса системы.

Главный момент сил инерции механической системы

Вычислим главный момент сил инерции системы.

Имеем(6.12)

так как , (а)

здесь - кинетический момент системы.Подставляя (а) в (6.12), получаем значение главного момента сил инерции(6.13)

Главный момент сил инерции твердого тела, вращающегося вокруг неподвижной оси

Главный момент сил инерции твёрдого тела, вращающегося, вокруг неподвижной оси, сводится к паре сил, момент которого равен(6.14)

где

Если ось вращения проходит через центр тяжести тела и оси xyzявляются главными осями, то(6.14а)

=17=

Момент инерции тела – характеристика инерции тела для его непоступательного движения.

Момент инерции этой точки относительно оси равен моменту инерции этого тела относительно той же оси.

Момент инерции тела относительно центра оси – плоскости.

-центр

- физический смысл оси ;-центр плоскости.

Центробежные моменты инерции- момент инерции, который учитывает неравномерность распределения масс относительно оси. Это единственный момент инерции , который может принимать положительные и отрицательные значения .

, ,

=18=

Радиус инерции()-величина определяемая из соотношения.

Радиус инерции- это расстояние от точки в которой условно сосредоточена масса тела до оси.

Определение моментов инерции тел в простейших случаях:

1)длинный тонкий стержень

2)однородный диск (масса распределена однородна)

Точка распределена по ободу

;

3)однородная пластина

;

=19=

Кинетическая энергия твердого тела. Теорема об изменении кинетической энергии системы

Твердое тело является частным случаем механической системы и рассматривается как непрерывно распределенная масса, тогда все суммы, входящие в выражение для кинетической энергии системы, переходят в интегралы. Так, для твердого тела формула (5.11) примет вид

. (5.14)

1. Кинетическая энергия твердого тела, двигающегося поступательно.

При этом виде движения скорости всех точек тела одинаковы (рис. 5.8). Вынося в формуле (5.14) за знак интеграла, получим

. (5.15)

Кинетическая энергия твердого тела, движущегося поступательно, равна половине произведения массы тела M на квадрат его скорости.

2. Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси

Модуль скорости V любой точки твердого тела, вращающегося вокруг неподвижной оси, равен , где - модуль угловой скорости твердого тела, - расстояние от точки до оси вращения z (рис. 5.9). Подставляя в формулу (5.14), получим

(5.16)

здесь – момент инерции твердого тела относительно оси z.

Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.

1. Кинетическая энергия твердого тела при плоско – параллельном движении

При плоско – параллельном движении скорость любой точки тела состоит из геометрической суммы скорости полюса и скорости точки при вращении вокруг полюса. Пусть тело движется плоско в плоскости Oxy, тогда

|| . За полюс выбираем центр масс тела, тогда в формуле (5.13), скорость есть скорость точки k тела при ее вращении относительно полюса (центра масс) и равна , где расстояние k-ой точки до полюса. Тогда (5.13) перепишется

Имея в виду, что – момент инерции тела относительно оси z, проходящей через полюс С, последнее выражение можно переписать как (5.17)

при плоско – параллельном движении тела кинетическая энергия складывается из кинетической энергии поступательного движения вместе с центром масс и кинетической энергии от вращения вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения.

Теорема об изменении кинетической энергии системы

Пусть точки системы массой переместились так, что их радиус-векторы в инерциальной системе отсчета получили приращение . Найдем, как при этом изменилась кинетическая энергия Т системы.

Согласно (5.11), кинетическая энергия системы

.Вычислим дифференциал кинетической энергии системы и преобразуем полученное выражение

здесь

Принимая во внимание, что , где - ускорение точки а и - равнодействующие внешних и внутренних сил, приложенных к точке, перепишем последнее равенство в виде

.

Таким образом, (5.23)

Последнее равенство выражает теорему об изменении кинетической энергии механической системы в дифференциальной форме: дифференциал кинетической энергии системы равен элементарной работе всех сил системы.

Частный случай. Для абсолютно твердого тела сумма работ всех внутренних сил системы равна нулю:

.Следовательно, теорему об изменении кинетической энергии (5.23) для твердого тела можно записать в виде(5.24)

Изменение кинетической энергии твердого тела при каком-либо элементарном перемещении равно элементарной работе внешних сил, действующих на тело.

Если обе части (5.24) проинтегрировать между двумя положениями – начальным и конечным, в которых соответственно кинетическая энергия и , получаем (5.25)

=20. =

Потенциальное силовое поле. Потенциальная функция. Поверхность равного потенциала. Работа силы в потенциальном поле.

Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке. Примером может служить поле силы тяжести Земли или поле сил сопротивления в потоке жидкости (газа). Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы.

Работа, которую совершают силы поля при перемещении частицы из точки 1 в точку 2, зависит, вообще говоря, от пути. Однако среди стационарных силовых полей имеются такие, в которых эта работа не зависит от пути между точками 1 и 2. Этот класс полей, обладая рядом важнейших свойств, занимает особое место в физике. Рассмотрим свойства таких полей.

Введем определение: стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называется потенциальным, а сами силы - консервативными.

Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными. К числу таких сил принадлежит, например, сила трения, так как работа этой силы зависит в общем случае от пути.

Покажем, что в потенциальном поле работа сил поля на любом замкнутом пути равна нулю. Действительно, любой замкнутый путь (рис. 5.5) можно разбить произвольно на две части: 1а2 и 2b1. Так как поле

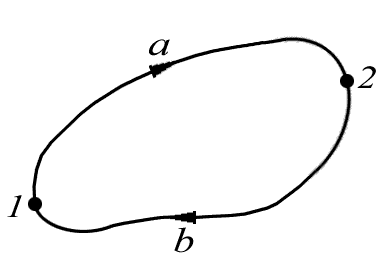
потенциально, то, по условию С другой стороны, очевидно, чтоПоэтому

что и требовалось доказать.

Наоборот, если работа сил поля на любом замкнутом пути равна нулю, то и работа этих сил на пути между произвольными точками 1 и 2 от формы пути не зависит, т. е. поле потенциально. Для доказательства выберем два произвольных пути: 1а2 и 1b2 (рис. 5.5). Составим из них замкнутый путь 1a2b1. Работа на этом замкнутом пути по условию равна нулю, т. е. ОтсюдаНо, поэтому

Таким образом, равенство нулю работы сил поля на любом замкнутом пути есть необходимое и достаточное условие независимости работы от формы пути, и может считаться отличительным признаком любого потенциального поля сил.

Рассмотрим важный случай поля центральных сил. Всякое силовое поле вызывается действием определенных тел. Сила, действующая на частицу А в таком поле, обусловлена взаимодействием этой частицы с данными телами. Если силы, зависят только от расстояния между взаимодействующими частицами и направлены по прямой, соединяющей эти частицы, от их называют центральными. Такими примерами служат силы гравитационные, кулоновские и упругие.

Центральную силу, действующую на частицу А со стороны частицы В, можно представить в общем виде: ,

где -функция, зависящая при данном характере взаимодействия только от r - расстояния между частицами;единичный вектор, задающий направление радиус-вектора частицы А

относительно частицы В

Докажем, что всякое стационарное поле центральных сил потенциально. Для этого найдем работу центральных сил в случае, когда силовое поле вызвано наличием одной неподвижной частицы B, а затем обобщим результат на произвольный случай. Элементарная работа силы (5.8)

на перемещении естьТак какпроекция векторана вектор, или на соответствующий радиус-вектор(рис. 5.6), тоРабота же этой силы на произвольном пути от точки 1 до точки 2

Полученное выражение зависит, очевидно, только от вида функции , т. е. от характера взаимодействия и от значений и- начального и конечного расстояний между частицамиA и B. От формы пути оно никак не зависит. Это и означает, что данное силовое поле потенциально.

Обобщим полученный результат на стационарное силовое поле, вызванное наличием совокупности неподвижных частиц, действующих на частицу A с силами .., каждая из которых является центральной. В этом случае работа результирующей силы при перемещении частицыA из одной точки в другую равна алгебраической сумме работ отдельных сил. А так как работа каждой из этих сил не зависит от формы пути, то и работа результирующей силы от нее также не зависит. Таким образом, действительно, любое стационарное поле центральных сил потенциально.

Введем понятие потенциальной энергии частицы в поле. То, что работа сил потенциального поля зависит только от начального и конечного положений частицы, дает возможность ввести чрезвычайно важное понятие потенциальной энергии.

Представим себе, что мы перемещаем частицу в потенциальном поле сил из разных точек P в фиксированную точку O. Так как работа сил поля не зависит от формы пути, то остается зависимость ее только от положения точки P (при фиксированной точке O ). А это значит, что данная работа будет некоторой функцией радиус-вектора r точки P.

Обозначив эту функцию , запишем

Функцию называютпотенциальной энергией частицы в данном поле.

=21=

Потенциальная энергия. Закон сохранения механической энергии.

Потенциальная энергия – это функция координат точек системы, она представляет собой работу сил поля по перемещению механической системы.

Через каждую точку поля можно провести одну эквипотенциальную поверхность.

При движении механической системы в потенциально-силовом поле полная энергия системы величина постоянная.

Потенциальная энергия материальной точки равна работе сил потенциального поля при переходе из данного положения в нулевое П=-U

=22.=

Квалификация связей.

Свободное тело-перемещение которого ничем не ограничено.

Связи- ограничения, накладываемые на возможные перемещения (скорости) различных тел. Как правило связи- это физические тела.

Связи : голономные связи – накладывают ограничение на положение точки, описавыется уравнением f(x₁y₁z₁)=0. Неголономные – накладывают ограничение на положение точки и её скорость, описываются уравнением f(x₁y₁z₁x^’₁y^’₁z^’₁)=0

Удерживающие связи допускают не только прямое, но и обратное перемещение.

Например стержень(двусторонние).

Неудерживающая(односторонняя). Н-р нить.

Ур-ие удерживающей связи: f(x;y;z)=0

Неудерживающие связи описывается уравнением f(x;y;z)*принадлежит*0

Стационарные связи: в Ур-ия которых время в явном виде не входит.

Геометрические связи: связи, Ур-ия которых содержат координаты точек.

Кинематические связи содержат координаты и скорость.(накладывают ограничения на положение тела и его скорость)

Идеальные связи: такие, работа р-ий которых на бесконечно малых возможных перемещениях равна 0

Например: гладкая поверхность, шарнир без трения и зазоров.

Обобщённые координаты, независимые между собой параметры q_i (r = 1, 2,..., s) любой размерности, число которых равно числу s степеней свободы механич. системы и которые однозначно определяют положение системы. Закон движения системы в О. к. даётся s уравнениями вида q_i = q_i (t), где t — время. О. к. пользуются при решении многих задач, особенно когда система подчинена связям, налагающим ограничения на её движение. При этом значительно уменьшается число уравнений, описывающих движение системы, по сравнению, например, с уравнениями в декартовых координатах. В системах с бесконечно большим числом степеней свободы (сплошные среды, физические поля) О. к. являются особые функции пространственных координат и времени, называются потенциалами и т.п.

=23=

Главный вектор и главный момент инерции.

К системе сил инерции действующих на систему материальных точек или твёрдое тело применим принцип Пуансо и приведём их к некоторому центру, при этом получим главный вектор сил инерции

и главный момент инерции

Приведение сил инерции к центру:

1)поступательное движение твёрдого тела. Силы инерции приводятся только к главному вектору (для точки С) и приложенному к центру масс.

2)вращательное движение плоской фигуры вокруг оси перпендикулярной плоскости фигуры:

, ,

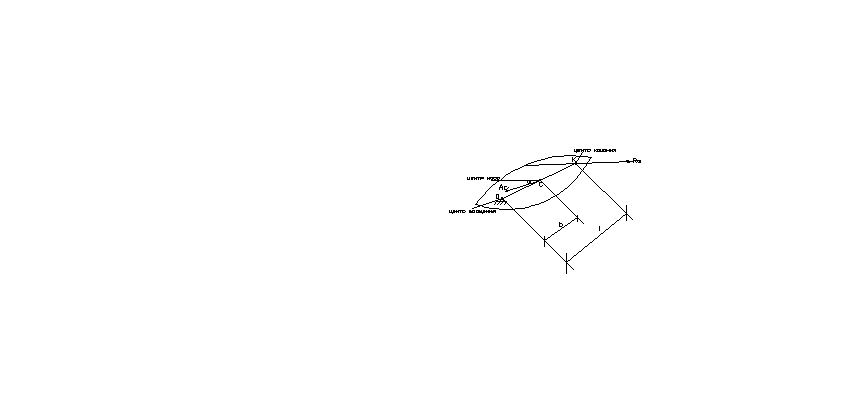
3)плоско - параллельное движение. Силы инерции приводятся к главному вектору приложенному к данному привидению и к главному моменту сил инерции.

На предыдущем рисунке в точке О: ,,если при вращательном движении центр масс совпадает с осью вращения, то, а главный момент:.

=24.=

Принцип Даламбера для М.Т., для механической системы.

Понятие о силе инерции.

Даламберова сила инерции - векторная величина, численно равная произведению массы точки на модуль её ускорения.

При криволинейном неравномерном движении точки

Принцип Даламбера для точки – позволяет задачи динамики решать средствами статики.

В каждый момент времени сумма сил активных, сил реакции связи и сил инерции, условно приложенных к точке равна нулю.

Принцип Даламбера для систем.

Сумма активных сил, сил реакции связи и сил инерции, условно приложенных к точкам системы, а также сумма моментов всех этих сил, относительно любого центра, должны быть равны нулю.

,

Где

-главный вектор активных сил

- главный вектор сил реакций связи

- главный вектор сил инерции

- моменты этих сил.

Порядок решения задач.

1.изображаем на схеме акт. силы

2. освобождаемся от связей, прикладываем реакции связей, налож. на каждую точку системы.

3.прикладываем силы инерции.

4. выбираем систему координат.

5. составл. ур-е равновесия для каждой из МТ, решаем систему ур-й.

=26=

Общее уравнение динамики.

Общее уравнение динамики относится к уникальному методу исследования задач динамики механических систем.

Рассмотрим голономную систему N материальных точек, подчиненную идеальным связям. Каждая точка системы движется согласно основному закону динамики

где – масса k-ой точки системы, – ее ускорение, – равнодействующая внешних сил, приложенных к k –ой точке (k=1,2,…,N).

Если ввести силу инерции то уравнение (6.1) можно записать в форме равновесия сил

Или(6.2)

Выражение (6.2) соответствует принципу Д‘Аламбера: совокупность всех внешних сил, действующих на механическую систему и сил инерции образует в каждый момент времени уравновешенную систему сил.

Мысленно зафиксируем время t и сообщим каждой точке системы одно из возможных перемещений Умножим скалярно каждое слагаемое уравнения (6.2) на , затем сложим между собой все N полученных уравнений между собой, получим

т.е. ,

6.3)

здесь: – элементарная работа внешних сил, на одном из возможных перемещений ; – элементарная работа сил инерции на том же возможном перемещении.

Уравнение (6.3) называется общим уравнением динамики:

при движении механической системы в каждый момент времени сумма элементарных работ всех действующих на систему внешних сил и сил инерции на любом возможном перемещении равна нулю.

Так как в уравнение (6.3) входит работа сил инерции, величина которой выражается через ускорение точек системы , то эти уравнения дают возможность составлять дифференциальные уравнения движения механической системы.

Если механическая система представляет собой абсолютно твердое тело и если это тело движется поступательно, то множество сил инерции точек тела следует заменить главным вектором сил инерции, приложенным к центру масс этого тела и равным

(6.4)

здесь М – масса тела, ускорение центра масс тела.

Если твердое тело вращается относительно неподвижной оси z, и ось вращения является главной центральной осью, то множество моментов от сил инерции следует заменить главным моментом сил инерции, равным

(6.5)

здесь – момент инерции тела относительно оси вращения, – угловая скорость.

Если твердое тело совершает плоское движение, то множество сил инерции всех точек заменяют главным вектором сил инерции, приложенным к центру масс этого тела и главным моментом сил инерции относительно центра.

=25=

Принцип возможных перемещений.

Положением равновесия называется такое положение системы, в котором система будет находиться все время, если в начальный момент времени она находилась в этом положении, и скорости всех ее точек были равны нулю.

Положение системы будет положением равновесия в том случае, когда в этом положении системы (5.1)

Равенство (5.1) выражает принцип возможных перемещений:

для того,чтобы стационарная механическая система с идеальными конечными связями находилась в положении равновесия, необходимо и достаточно, чтобы в этом положении сумма элементарных работ внешних сил на любых возможных перемещениях системы равнялась нулю.

Принцип возможных перемещений был известен со времен Архимеда под названием ˝золотого правила механики˝ и применялся к простейшим механизмам. Рассмотрим в качестве примера рычаг Архимеда Рычаг имеет одну степень свободы – может вращаться вокруг точки О. Равновесие имеет место, когда элементарная работа при повороте рычага на элементарный угол равна нулю.

Имеем

Поэтомуили ,

выигрыш в силе компенсируется проигрышем в перемещении и наоборот – золотое правило механики.

Принцип возможных перемещений можно применять для определения реакций опор (реакций связей). Для этого связь, реакцию которой необходимо определить, отбрасывают (освобождают систему от этой связи), заменяя ее силой реакции. Эту силу добавляют к внешним силам. Оставшиеся связи должны быть идеальными. Неидеальную связь заменяют идеальной, компенсируя неидеальность соответствующими силами. Так, если связью тела является шероховатая поверхность, то ее заменяют гладкой поверхностью, добавляя к внешним силам силу трения скольжения.

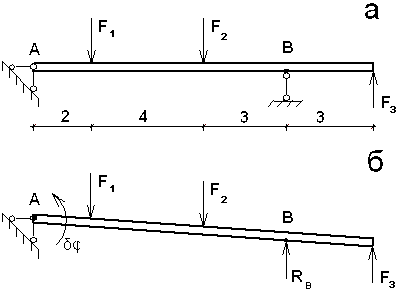
Пример 1. На тело АВ, лежащее на шарнирных опорах А и В, действует нагрузка, как показано на Определить реакцию шарнира В, если F₁=10 кH, F₂=20 кH, F₃=30 кH. Все размеры показаны на рисунке в метрах.

Решение. На заданное тело АВ наложено три связи. Мысленно отбросим шарнирно – подвижную опору В, т. е. одну связь, заменив ее действие искомой реакцией Реакция становится внешней силой. Прикладываем к телу все заданные силы.

Система приобрела одну степень свободы. Теперь на тело наложено две связи. Тело АВ под действием внешних сил будет вращаться в плоскости вокруг шарнира А, возможным перемещением балки будет ее поворот вокруг шарнира А. Повернем балку, например, против хода часовой стрелки на , т. е. зададим системе возможное перемещение.

Запишем принцип возможных перемещений (5.1). Каждое слагаемое в полученном уравнении будет представлять собой элементарную работу, совершаемую соответствующей внешней силой.

Имеем

,

отсюда

Ответ:

Модуль реакции , направлена реакция вниз.

=27=

Уравнение Лагранжа 2-го рода

∑δA_i^a+∑δA_i^u=0

Q^a=∑δA^a_i / δq; Q^u=∑δA^u_i / δq следовательно

Q^aδq+Q^uδq=0

(Q^a+Q^u)δq=0; δq не равно 0; следовательно Q^a+Q^u=0

-Q^u=Q^a

Представим обобщенную систему сил, зависящую от сил инерции через массу тел системы, ускорение и возможное перемещение с помощью преобразований получаем уравнение Лагранжа 2-го рода:

d/dt(δT/δq)-δT/δq=Q

Производная по времени от частной производной кинетической энергии до обобщенной скорости минус частная производная кинетической энергии по обобщенной координате равно обобщенной силе.

T-кинетическая энергия системы в ее текущем положении

q-обобщенная координата

q-обобщенная скорость

Q- обобщенная сила системы

Q=∑δA_i / δq

=33=

С кинематической точки зрения удар характеризуется скоротечностью процесса и значительным изменением скорости ,при незначительном изменении координаты, с динамической точки зрения, удар характерезуется мгновенным возникновением значительных по величине импульсов.

При ударе необходимо учитывать не только силы вызывающие удар ,но и вид движения тел при ударе, а также и материял удоряемого тела.

В простейших случаях удар это практически мгновенное приложение либо снятие связей.

Простейшие виды удара

1) Столкновение 2 тел одно из которых движется поступательно.

2) Отрыв части тела приведший к вращению.

3) Ковка,штамповка забивание сваи

Основной характеристикой при ударе является ударный импульс,

Рассмотрим 2 тела двигающиеся в одном напровлении;

V₁>V₂

V₁-U _{фаза диформаций, скорость первого тела- V1}¹

V₂-U ¹

Действие ударной силы на материальную точку.

Во время удара как правило силами не ударного характера принебригают.

Теорема об изменении количества движения системы при ударе ,для первой точки где,

Для ? системы применение количества движения системы за некоторый промежуток вренени равно ветторной сумме внешних ударных импульсов приложенных к точкам системы.

Теорема о изменении количества движения

Изменение момента количества движения системы при ударе ,за время удара равно сумме моментов внешних ударных импульсов за то же время

Запишем теорему о изменении момента количества движения

Момент относительно оси z_а и z_b = 0 т.к.эти импульсы пересекают ось

Определение угловой скорости вращения после удара

Угловая скорость вращения после удара изменяется на величину ран\вную моменту импульса относительно той же оси.

=34=

Действие ударной силы на материальную точку. Теорема об изменении количества движения материальной точке при ударе.

mU –mV = S

_ _ _

m(U – V)= S

_ _ _

U – V= S

_ _ _

U=S / m +V

Во время удара как правило силами неударного характера пренебрегают.

Теорема:

На некоторую систему материальных точек действуют ударные силы.

Пусть ν_i-скорость до удара

U_i- после удара

Следовательно:

mU_i – mV_i = S_i^e + S_iⁱ

∑mU_i - ∑mV_i = ∑S_i^e + ∑S_iⁱ

∑S_iⁱ=0 следовательно K-K_o=∑S_i^e

K,K_o- количество движения из начального положения в конечное

Изменение количества движения системы при ударе равно геометрической сумме внешних ударных импульсов, действующие на точки системы.

_ _

r_c= ∑m_ir_i / M

_ _

M_rc= ∑r m_i r_i

_{_ _ _ _}

Mdr_c / dt=∑m_i dr_i /dt следовательно MV_c= m_iV_i

_{_ _}

MU_c – MV_c = ∑S^e_i

=35. =

Теорема об изменении кинетического момента механической системы при ударе.

m_kU_k - m_kU_{k =} S^e_k + Sⁱ_k

(r _k×m_kU_k) – (r _k×m_kV_k) = (S^e_k×r _k) + (Sⁱ_k×r _k)

∑(r _k×m_kU_k) – ∑(r _k×m_kV_k) = ∑(S^e_k×r _k) +∑ (Sⁱ_k×r _k)

I – I₀ = ∑m₀(S^e_k) + ∑m₀(Sⁱ_k)

L_z - L_{zo =} ∑m_z(S^e_k)

Если ∑m_z(S^e_k) = 0 то L = const

Изменение момента количества движения системы при ударе за некоторый промежуток времени равно сумме моментов внешних ударных импульсов за тоже время.

=36. =

Теорема об изменении количества движения механической системы при ударе.

Для одной точки

τ τ

mU-mV=∫ Fdt+ ∫F*dt

0. 0

F*-сила неударного характера

∑m_kU_k - ∑m_kτ_k=∑Fdt + ∑F*dt

K- K₀=∑S_k

Для идеальной системы изменение количества системы занимает промежуток времени равный векторной сумме внешних ударных импульсов приложенных к точке системы.

K_y –K_0y=∑S^e_ky

Если ∑S^e_kx=0 то kx=const

Если ∑S^e_ky=0 то ky= const

=37=

Запишем теорему об изменении количества движения системы:

; , так как эти импульсы пересекают ось.

,

Последняя формула-определение угловой скорости вращения после удара.

Угловая скорость вращения тела после удара изменяется на величину, равную отношению момента ударного импульса к моменту инерции тела относительно той же оси.

Чтобы избежать возникновения ударных реактивных импульсов в опорах, ударный импульс должен быть приложен в центре удара, так как лежащая в плоскости z, a, y, отстоящая оси вращения на расстоянии , при этом точка К располагается в плоскости, проходящей через точку О, для которой осьz главная ось инерции.

=38=.

Удар тела о неподвижную поверхность. Линия удара, центральный, косой удар. Коэффициент восстановления при ударе.

Центр масс тела до удара лежит на общей нормали n тела и неподвижной поверхности, скорость v тела до удара направлена по этой нормали (а);

Ударная сила – мгновенная реакция поверхности Nуд.

Удар делится на две фазы:1) от момента прикосновения тела к поверхности до момента полной остановки тела в деформированном состоянии. m-масса тела: -длительность фазы

2)От конца фазы первой фазы до момента когда тело отделяется поверхности со скоростью u, частично восстанавливая свою форму:

Для скоростей имеется соотношение - коэффициент восстановления.

Для реальных веществ 0<K<1

=39=

Где V-скорость до удара; U-скорость после удара;

-угол до падения; - угол отражения.

По теореме об изменении количества движения :

Спроецируем это уравнение на ось тангенсов:

, .

Спроецируем тоже уравнение на ось нормалей:

(1)

, подставим V и U в формулу (1) получим:

=40=

В случае абсолютно неупругого удара потери кинетической энергии механической системы равны кинетической энергии системы, если бы её тела двигались с потерянными скоростями:

, где -скорости тел системы до удара,-скорости тел системы после удара для абсолютно неупругого удара.

Для частично неупругого удара:

, где к- коэффициент упругости .

Для случая когда , то, если, то тело 1 больше по массе (пример: забивка сваи или гвоздя).

тело 2 больше по массе (пример: ковка металла).

=41=