§ 7. Модальные логики

В классической двузначной логике рассматривались простые и сложные ассерторические суждения, т. е. такие, в которых не установлен характер связи между субъектом и предикатом, например: “Морская вода соленая” или “Дождь то начинал хле­стать теплыми крупными каплями, то переставал”.

В модальных суждениях раскрывается характер связи между субъектом и предикатом или между отдельными простыми суждениями в сложном модальном суждении. Например: “Необходимо, что металлы - проводники электрического тока” или “Если будет дуть попутный ветер, то, возможно, мы приплывем в гавань до наступления темноты”.

Модальными являются суждения, которые включают мо­дальные операторы (модальные понятия), т. е. слова “необхо­димо”, “возможно”, “невозможно”, “случайно”, “запрещено”, “хорошо” и многие другие (см. главу III, § 6 “Деление сужде­ний по модальности”). Модальные суждения рассматривают­ся в специальном направлении современной формальной ло­гики - в модальной логике.

Изучение модальных суждений имеет длительную и многогран­ную историю. Мы отметим лишь некоторые из ее аспектов. Мо­дальности в логику были введены Аристотелем. Термин “воз­можность”, по Аристотелю, имеет различный смысл. Возможным он называет и то, что необходимо, и то, что не необходимо, и то, что возможно. Исходя из понимания модальности “возможность”, Аристотель писал о неприменимости закона исключенного тре­тьего к будущим единичным событиям.

Наряду с категорическим силлогизмом Аристотель исследу­ет и модальный силлогизм, у которого одна или обе посылки и заключение являются модальными суждениями. Я. Лукасевич в книге “Аристотелевская силлогистика с точки зрения современ­ной формальной логики” две главы посвящает аристотелевской модальной логике предложений (гл. VI) и модальной силлоги­стике Аристотеля (гл. VIII)'. Аристотель рассматривает модаль­ную силлогистику по образцу своей ассерторической силлоги­стики: силлогизмы подразделяются на фигуры и модусы, неправильные модусы отбрасываются с помощью их интерпре­тации на конкретных терминах.

Согласно Аристотелю, случайность есть то, что не необхо­димо и не невозможно, т. е. р -случайно означает то же самое, что ир -не необходимо ир -не невозможно, но Лукасевич отмечает, что аристотелевская теория случайных силлогизмов полна серьезных ошибок². Итог исследований Лукасевича та­кой: пропозициональная модальная логика Аристотеля имеет ог­ромное значение для философии; в работах Аристотеля можно

_____________________________

'Lukasiewicz J. Aristotle's Syllogistic from the Standpoint of Modem Formal Logic. ClarendonPress.Oxford, 1957;Лукасевич Я.Аристотелевская силлоги­стика с точки зрения современной формальной логики. М., 1959.

²Ibid.Ch. VIII. § 60.

найти все элементы, необходимые для построения полной систе­мы модальной логики; однако Аристотель исходил из двузначной логики', в то время как модальная логика не может быть двузнач­ной. К идее многозначной логики Аристотель подошел вплотную, рассуждая о “будущем мореном сражении”. Следуя Аристотелю, Лукасевич в 1920 г. построил первую многозначную (трехзнач­ную) логику. Так осуществляется связь модальных и многознач­ных логик.

Значительное внимание разработке модальных категорий уде­ляли философы в Древней Греции и особенно Диодор Крон, рас­сматривавший модальности в связи с введенной им временнбй переменной. В средние века модальным категориям также уделя­лось большое внимание. В XIX в. категорию вероятности разрабатывали Дж. Буль и П. С. Порецкий.

Возникновение модальной логики как системы датируется 1918г., когда американский логик и философ Кларенс Ирвинг Льюис (1883-1964) в работе “ASurveyofSymbolicLogic” сформулировал модальное исчисление, названное им впослед­ствии S3.

В книге “SimbolicLogik”, написанной им совместно с К. Лэнгфордом в 1932 г., он сформулировал еще пять модальных логиче­ских систем, связанных с S3 и между собой. Это - системыS1,S2,S4,S5,S6.

Приведем описание модальной системы S1².

I. Исходные символы:

1. р, q, rи т. д. - пропозициональные переменные;

2. ~ р -отрицаниер

3. р* q –конъюнкцияpиq;

4. рq - строгая импликация льюисовской системы;

5. ◊р- модальный оператор возможности (возможноp);

6. р = q -строгая эквивалентность,р=qравносильно ( рq)*(qp)

_____________________________

'Отметим, что этот теперь общепринятый термин - “двузначная логика” -был введен Лукасевичем.

²Cм.-.LewisC.J^LandfordC.H. Symbolic Logic. NewJork, 1932.P. 123-126. В их работе вместо скобок стоит знак “ • ”, мы же употребляем скобки.

II. Аксиомы системы S1:

1) p*qq*p;

2) p*qp;

3) pp*p;

4) (p*q)*rp*(q*r),

5) р~ ~ р;

6)(pq)*(qr)[pr};

7) p*(pq)q.

Аксиома 5 может быть выведена из остальных, как было по­казано позднее. Так как конъюнкция связывает “сильнее”, чем импликация, то скобки можно опустить или заменить их точка­ми; как это сделано у Льюиса.

III. Правила вывода S1:

1) Правило подстановки. Любые два эквивалентных друг дру­гу выражения взаимозаменимы.

2) Любая правильно построенная формула может быть подставлена вместо р,илиq.или r и т. д. в любом выражении.

3) Если выводим о ри выводим оq,то выводимор • q .

4) Если выводим о ри выводим орq ,то выводимоq.

Льюис построил модальную пропозициональную логику S1 в виде расширения немодального (ассерторического) пропозицио­нального исчисления. При этом основные черты S1 и других его исчислений были скопированы с формализованной логической системыPrincipiaMathematicaРассела и Уайтхеда, сформули­рованы с помощью понятий, только терминологически отличаю­щихся от понятий, использованных вPrincipiaMathematica. Кро­ме Рассела и Уайтхеда, идеи классической логики развивали многие современные математические логики, например, амери­канский логик и математик С. Клини'. Исчисления Льюиса по-

____________________________

'Kleene S. С. Mathematical Logik. New York - London - Sydney, 1967.

строены аксиоматически по образцу Principia, и по аналогии сPrincipiaЛьюис доказывает ряд специфических теорем.

В классической двузначной логике логическое следование отождествляется с материальной импликацией и допускают­ся такие формы вывода:

p→ (q→p).(1)

т. е. истинное суждение следует из любого суждения (“исти­на следует откуда угодно”),

p→(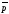→q) (2)

т. е. из ложного суждения следует любое суждение (“из лжи сле­дует все, что угодно”). Это противоречит нашему содержательно­му, практическому пониманию логического следования, поэтому данные формулы, как и некоторые другие, и соответствующие им принципы логического следования называются парадоксами ма­териальной импликации.

Льюис создал свои новые системы с целью избежать этих парадоксов и ввести новую импликацию, названную им “стро­гой импликацией”, такую, чтобы логическое следование представлялось не чисто формально, а по смыслу (содержатель­но) и новая импликация была ближе к связке естественного язы­ка “если, то”. В строгой импликации Льюиса рqневозможно утверждать антецедент, т. е.р,и отрицать консеквент, т. е.q ¹.

В системах Льюиса были устранены парадоксы материаль­ной импликации, т.е. формулы (1) и (2) стали невыводимыми, но появились парадоксы строгой импликации. К ним относятся, например, такие формулы:

(~ ◊ ~p)(q p) (3)

(~ ◊ p) (p q) (4)

Итак, отождествлять строгую импликацию Льюиса со следова­нием нельзя.

________________________

'Антецендент - первый член импликации, которому предпослано слово “если”. Консеквент - второй член импликации

С целью исключить парадоксы строгой импликации Льюиса немецкий математик и логик Ф. В. Аккерман (1896 -1962) по­строил свою систему модальной логики. Он ввел так называемую сильную импликацию, которая не тождественна строгой имплика­ции Льюиса, и модальные операторы Аккермана и Льюиса также не являются тождественными. Аккерман все логические терми­ны и модальные операторы определяет через сильную импликацию так: NAравносильно→λ,МАравносильно.ЗдесьА -любая правильно построенная формула системы Аккермана;N-оператор необходимости;М-оператор возможности;-от­рицаниеA; → обозначает сильную импликацию;-логическая постоянная, обозначающая “абсурдно”. Эта постоянная в свою очередь определяется так:А&,где&обозначает конъюнк­цию. И последняя формула читается так: из противоречия, т. е.А ине-А,следует абсурд. В системе Аккермана не выводятся фор­мулы, структурно подобные парадоксам материальной или строгой импликации.

Системы Льюиса и Аккермана являются бесконечнозначными. В отличие от этих систем первоначально построенные сис­темы Лукасевича являются конечнозначными: одна - трехзначная (1920), другая - четырехзначная (1953). В четырехзначной системе Лукасевича¹также обнаружены парадоксы. Главный из них состоит в том, что ни одно аподиктическое предложение не истинно, т. е. ни одно суждение видаL(гдеLобозначает не­обходимость, а -любая формула) не является истинным. Это означало бы, что необходимых суждений нет, т. е. модальный оператор “необходимо” упраздняется. Лукасевич пишет: “Лю­бое аподиктическое предложение должно быть отброшено”². Сам Лукасевич считал это достоинством своей системы, а понятие “необходимость” - псевдопонятием. С такой точкой зрения, ко­нечно, согласиться нельзя.

Интерпретации модальных логик различны. Известный авст­рийский философ и логик Р. Карнап (1891-1970) пытался ин­терпретировать модальные понятия (операторы) с помощью так

____________________________

'См.' Lukasiewicz J. Aristotle's Syllogistic from the Standpoint of Modem For­mal Logik. ClarendonPress.Oxford, 19S7.Ch. VII;Лукасевич Я.Аристотелев­ская силлогистика с точки зрения современной формальной логики. М., 1959.

4bid.Ch. VII. § 50.

называемой теории “возможных миров”, в которой допускается наличие множества “миров”, один из которых -действительный, реальный мир, а остальные - возможные миры. Необходимым объ­является то, что существует во всех мирах, возможным - то, что существует хотя бы в одном.

Р. Карнап в 1946 г., используя понятие “описание состояния”, предложил интерпретацию модальных операторов, в основе кото­рой лежала идея различия возможного и действительного мира.

В ином направлении шел финский логик Я. Хинтикка. Крити­чески переосмыслив введенное Карнапом понятие “описание состояния”, он разработал технику “модальных множеств”, т. е. миров (1957), - оригинальную семантическую концепцию возмо­жных миров. Разработка семантики возможных миров для мо­дальных логик продолжается.

Разнообразными проблемами модальной логики занимается американский логик Р. Фейс'.

В настоящее время разработаны многие виды модальностей, ко­торые отражены в таблице, помещенной на с. 97 данного учебника.

Теорией модальных логик и построением новых модальных логических систем активно занимаются логики А. А. Ивин², Я. А. Слинин³, Б. С. Чендов⁴,0. Ф. Серебряников, В. Т. Павлов и др.