Patai S., Rappoport Z. 1997 The chemistry of functional groups. The chemistry of double-bonded functional groups / 1355 149

I. INTRODUCTION

This monograph covers the period 1989 1995 and is partially an update of the work by Schaumann1. The scope is essentially the same, attention being focused primarily on thioaldehydes (thials) and thioketones (thiones). In keeping with the spirit of Reference 1, only some new developments in the field of thioketene, hetero cumulene and thioquinone chemistry are considered. Because of the fast evolution in the field, the spirit is somewhat different and physicochemical and theoretical topics are emphasized. Whenever possible, systematic comparisons with homologous carbonyl compounds, a natural yardstick, are

photophysics11,12, photochemistry11,13,14, radical reactions15,16, mass spectrometry17, photoelectron spectroscopy18 and electrochemistry19 of various families of thiocarbonyl compounds.

The last seven years have also witnessed important developments in the field of thiocarbonyl chemistry. Synthetic and reactivity studies have maintained their steady growth. New or improved experimental methods have been applied to the study of the physicochemical properties of these compounds as well as to the generation and observation of important fleeting species. In particular, flash vacuum thermolysis (FVT or FVP)20 and neutralization reionization mass spectrometry21 22.

Thanks to advances in computer technology, a number of theoretical studies have been performed that shed light on structural and spectroscopic properties as well as on the reactivity of thiocarbonyl compounds both in the ground and in excited electronic states.

In this review, quantitative aspects of the structure and reactivity of these compounds are treated first. New developments in the fields of synthesis and reactivity are examined next. As a consequence of their relevance for the development of new materials23 27 and the possibilities they offer for analytical purposes, the number of studies in which thiocarbonyl compounds act as ligands of a variety of metal ions has increased in an almost explosive way. Recent reviews28 30 are also available on specific families of coordination compounds involving thiocarbonyl ligands. A concise survey of the present status of these studies is presented in the last section.

1358 M. T. Molina, M. Ya´nez,˜ O. Mo,´ R. Notario and J.-L. M. Abboud

When warranted by their importance, mention shall be made of the biological or technological aspects of some compounds and reactions. A serious effort was made in order to minimize overlaps with previous reviews.

II.ENERGETICS AND STRUCTURE OF THIOCARBONYL COMPOUNDS. THEIR INFLUENCE ON REACTIVITY AND PHYSICAL PROPERTIES

A.Molecular Properties

As indicated earlier, quantum-mechanical methods, particularly molecular orbital (MO) treatments, are tools used to explore essentially all fields of thiocarbonyl chemistry. Hence, we shall first review the current status and scope of this methodology with respect to a number of important topics. This shall be followed by a survey of the experimental and theoretical data available on the thermodynamics, structure and selected aspects of the reactivity of these compounds.

1.Quantum mechanical studies

a. Molecular orbital (MO) treatments. These theoretical studies are not free, in some cases, from discrepancies between theory and experiment, as we shall illustrate later. Most of these discrepancies simply reflected the inadequacy of the theoretical model used to study a particular problem. We have thus considered it useful to provide a short analysis of the performance of the theoretical models most often used in the framework of ab initio molecular orbital theory, in order to outline the minimal computational requirements necessary to get reliable theoretical predictions when dealing with sulfur compounds in general and with thiocarbonyl compounds in particular.

Since in many instances we shall try to compare the properties of thiocarbonyl compounds with their carbonyl analogs, we recall that, in general, the theoretical treatment of sulfur containing systems is more demanding, essentially because of the larger number of electrons in the sulfur atom. This has restricted the ab initio calculations to relatively small compounds or to the use of small basis sets. Until quite recently, high level ab initio calculations were only reported for a few, small thiocarbonyl systems.

An adequate description of the geometries and electronic properties of sulfur containing compounds requires the inclusion of supplementary d functions in the basis set. Some theoretical work has explicitly analyzed the role of these supplementary d functions, in

particular for hypervalent molecules. Patterson and Messmer31, by means of a generalized valence bond (GVB) treatment of sulfur oxides, concluded that the role of d functions on the S atom is primarily to allow the orbitals to attain their optimum shapes while remaining mutually orthogonal. This implies that the orbitals obtained with a basis set supplemented with d functions are more flexible and are wrapped around the cores more effectively than those obtained from a basis without d functions, thus maximizing the electron nuclear attraction. They also concluded that the role of d functions in electronic structure calculations of hypervalent molecules differs from that in normal molecules, where they act as polarization functions. This conclusion is somewhat at variance with that by Magnusson32, who found that although the level of participation of supplementary d functions in the wavefunctions of hypervalent systems is greater than in normal molecules, there is no difference in the role of the d functions, which are required to properly respond to the rapidly varying molecular potential in the internuclear space. In any case, both studies clearly illustrate the need of including d functions in the treatment of sulfur containing systems. In later work Magnusson33 has shown that whether molecules are hypercoordinated or not, d functions provide a fairly constant 13 kcal mol 1 of the MP4 correlation energy per valence shell electron pair. He also showed that while for Hartree Fock calculations d functions behave as polarization functions, for correlated

calculations their major role is to provide angular correlation. Furthermore, the d function role in the correlated wavefunction seems to be quite independent of the sp basis set level.

In summary, it seems well established that supplementary d functions are indispensable in molecular orbital calculations of sulfur containing compounds. This is particularly true for thiocarbonyl compounds, wherein the anisotropy of the electrondensity distribution around sulfur is significantly greater34 than that around oxygen in carbonyl systems.

The need for a well-balanced basis set for the theoretical treatment of sulfur derivatives is also clear. In particular, a proper description of the angular correlation cannot be achieved by including supplementary d functions exclusively on the sulfur atom since, as has been shown by Magnusson33, supplementary functions on peripheral atoms (for instance O in SO2) contribute more to the correlation energy than the functions centered on the central sulfur atom. Similarly, some discrepancies between Hartree Fock optimized geometries for 6-thioguanine obtained when d functions are included exclusively in the sulfur atom35 with regards to those obtained when d functions are centered on all heavy atoms of the molecule36, may have their origin in the unbalanced character of the former basis set.

Not all the molecular properties present the same sensitivity to details of the basis set used to expand the molecular wavefunction. Thus, Alkorta37 analyzed the geometric and electronic properties of 22 sulfur compounds by means of ab initio calculations and local density functional (LDF) methods. He showed that, while a minimal STO-3G(d) basis set yields standard deviations of 0.033 A˚ for the bond lengths and 3.595° for the bond angles, the standard deviations when a 6-31G(d) basis set is used are reduced to 0.012 A˚ and 1.688°, respectively. However, both basis sets behave rather poorly as far as the dipole moments are concerned. The STO-3G(d) calculations yield too small values for this magnitude, with a standard deviation of 0.558 D, while the 6-31G(d) calculations predict dipole moments which are too large, with a standard deviation of 0.315 D, which does not change significantly when a second set of d functions is added to the basis set. It is only when electron correlation effects are taken into account, at the secondorder Møller Plesset perturbation theory [MP2/6-31G(d) level], that the calculated dipole moments come closer to the experimental values. For this set of compounds, the LDF results provide, in average, the best dipole moments of all methods analyzed in that paper, though it consistently yields too large bond distances for the atoms bonded to sulfur. Although there are in the literature systematic studies of the performance of different density functional methods to describe molecular properties of first-row compounds38, there is no similar study for sulfur containing systems. Nevertheless, density functional methods will likely become a very good and economic alternative to the standard ab initio methods.

It is fortunate that the trends of structural effects on the structures of thiocarbonyl compounds are largely basis-independent. Important examples shall be discussed later.

Abboud and coworkers39 have found the CDS bond length to vary within very narrow limits (1.60 A˚ š 0.1 A˚) for a wide set of thiocarbonyl derivatives, which includes 27 different molecules as well as substituents of different nature [CH3, OH, NH2, OCH3, F, Cl, SCH3, NHCH3, N(CH3)2, C2H5, OC2H5]. Similar behavior is observed when comparing the CDS optimized bond lengths for thiocarbonyl cyanide40, thiopropynal40 and thioformyl cyanide41. These findings are consistent with the conclusions of Mo´ and collaborators42 in the sense that the electronic charge density at the CDS bond critical point, for the same series of compounds, is also quite insensitive to the nature of the substitutent. In this respect, it is worth noting that the thiocarbonyl group, similarly to the carbonyl group43, is hard to perturb42. However, the thiocarbonyl group seems to conjugate better than the carbonyl group. Actually, the most significant structural difference between carbonyl and thiocarbonyl cyanide is that the C C bond is significantly shorter

1360 M. T. Molina, M. Ya´nez,˜ O. Mo,´ R. Notario and J.-L. M. Abboud

in the latter (1.437 A˚ vs 1.462 A)˚ while the corresponding stretching force constant is significantly higher (5.687 vs 5.076 mdyne/A)˚ 40. Something similar is found when the C C bond lengths in propynal and formyl cyanide are compared with those in thiopropynal40 and thioformyl cyanide, respectively. The significant shortening of the C C bond adjacent to the CDS linkage is presumably due40 to the release of electron density into the conjugated system, which is more favorable in the case of thiocarbonyl compounds because of the smaller electronegativity of sulfur.

b. Electron correlation effects. From the discussion in the preceding section it seems clear that some molecular properties, and in particular a correct description of the electronic charge distribution of the molecule, require unavoidably to take into account electron correlation effects. However, these effects are also important in obtaining reliable structures and energetics.

(i) Effects on structures. Correlation effects on molecular geometries are, in general, not negligible. For instance, geometries obtained at the MP2 level are in very good agreement with the experimental structures when a 6-31G(d) basis set is used44. Similarly, when the comparison of experimental and theoretical structures is carried out in terms of the rotational constants, the MP2/6-31G(d) values present a relative error ten times smaller than that found at the HF/6-31G(d) level45.

The computational cost is considerably higher when the geometry optimization is carried out at the correlated level rather than at the Hartree Fock level. We draw attention, however, to the fact that some aspects of the molecular structures can only be reproduced when electron correlation effects are taken explicitly into account. The fluoro, chloro and bromo disubstituted derivatives of thioformaldehyde are a paradigmatic example. The CDS bond of thioformaldehyde is reduced by about 0.020 A,˚ 0.010 A˚ and 0.014 A˚ in thiocarbonyl difluoride, dichloride and dibromide, respectively46 51. This experimental finding is not reproduced by Hartree Fock calculations52 which predict the CDS bond to be elongated by 0.006 A˚ on going from CBr2S to CF2S, contrary to experimental observation. Only when electron correlation effects are taken into account, at the MP2/6- 311G(d,p) level, is the experimental trend fairly well reproduced52 (shortenings of 0.020, 0.008 and 0.013 A,˚ respectively).

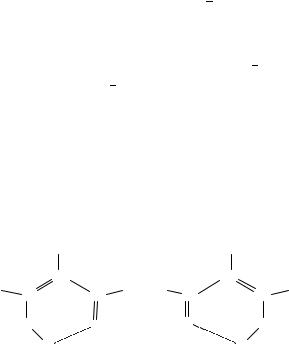
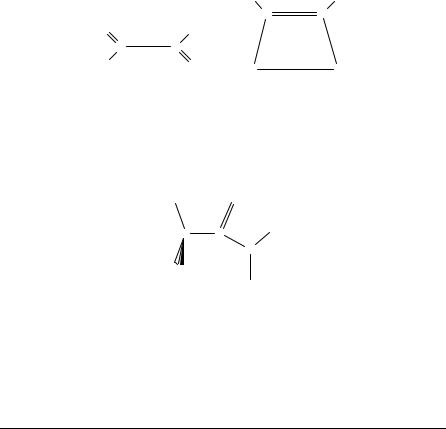
Significant changes in optimized geometries due to electron correlation contributions are also of relevance for systems which present intramolecular hydrogen bonds. We shall present here, as a suitable example, the case of monothiomalonaldehyde (1a) and its thienol tautomer (1b), since in this case the characteristics of the intramolecular hydrogen bonds depend strongly on the inclusion of electron correlation effects in the theoretical treatment.

In Table 1 we present the optimized geometries of both systems obtained at the HF level by using a triple zeta plus polarization basis set53 and at the MP2/6-31 C G(d,p)

1362 M. T. Molina, M. Ya´nez,˜ O. Mo,´ R. Notario and J.-L. M. Abboud

level54. It can be seen that differences between both sets of values are sometimes greater than 0.05 A˚ for bond lengths and greater than 3° for bond angles, respectively. However, the most dramatic changes affect the hydrogen bonds, which upon inclusion of electron correlation effects become more than 0.2 A˚ shorter. As we shall discuss in forthcoming sections, these structural changes will be reflected by the energetics of the corresponding hydrogen bonds.

Other valence tautomerisms such as that between 1,2-dithioglyoxal (2a) and 1,2-dithiete (2b), are also interesting examples of dramatic effects of electron correlation on optimized structures. As illustrated in Table 2, only optimizations carried out at the MP2 level, using either a 6-31G(d) or a 6-31CG(d,p) basis set55,56, are able to reproduce correctly the experimental bond lengths of the most stable conformer, 1,2-dithiete, while HF optimizations yield too short C C bond lengths and too long C S linkages.

Electron correlation effects have been found to be also significant as far as the internal rotation of thioamides is concerned57. MP2/6-31G(d) geometry optimizations57 indicated the eclipsed conformer (3) as the stable structure of thioacetamide, while this conformer was predicted to be a first-order saddle point at the HF/6-31G(d) level57.

H S

H

C C

N

H H

H

(3)

Very few geometry optimizations of thiocarbonyl derivatives have been carried out at a level higher than MP2/6-31G(d). Table 2 clearly shows, for the particular case of 1,2- dithiete (2b), that the effect of enlarging the basis set from 6-31G(d) to 6-31 C G(d,p) has very little effect on the optimized geometry. Something similar has been found by

TABLE 2. Ab initio optimized geometries for 1,2-dithiete (2b) (bond lengths in A,˚ bond angles in degrees)

TABLE 3. MP2-optimized geometries for some thiocarbonyl derivatives XYCDS (bond lengths in A,˚ bond angles in degrees)

aThese values correspond to a CCSD(T)/TZP geometry optimization. bC N bond length.

Csaszar41 for thioformyl cyanide, when comparing MP2/6-31G(d,p) and MP2/6-311G(d,p) optimized structures (see Table 3).

Table 3 also shows the negligible differences between MP2/6-31G(d) and MP2/6-31 C G(d,p) optimized geometries for thioformaldehyde and some monosubstituted derivatives. Table 3 includes also the optimized geometry for thioformaldehyde reported by Martin’s group58. This optimized geometry was obtained using the coupled cluster method with all single and double excitations augmented with a perturbative estimate of the effect of triplet excitations [CCSD(T)]. The close agreement between this CCSD(T) optimized geometry and the MP2 ones clearly illustrates the rather small effects of correlation contributions beyond second order. Hence, we may conclude that, in general, the MP2/6- 31G(d) approach will provide reasonably accurate structures for thiocarbonyl compounds, although for anionic species the MP2/6-31 C G(d) structures should be more reliable59, since a proper description of the electronic charge distribution of anions requires the inclusion of diffuse functions in the basis set60.

(ii) Effects on the energetics. Electron correlation effects are particularly important as far as the energetics of the systems is concerned. Sulfur containing compounds provide also good examples to illustrate this point.

The thiol thione tautomerism is particularly sensitive to the inclusion of these effects. Unfortunately, there are not many theoretical studies on this tautomerism in which electron correlation effects are included. In most studies, they are considered only for the evaluation of the total energies but using HF optimized structures. It is generally agreed, however, that electron correlation effects cannot be neglected if reliable results are sought in these systems36. This has a physical basis, related to the fact that in thiol/thione tautomerism there is a significant change in the nature of the bonds on going from the thiol, which has a S H bond, to the thione, where the S H bond has been replaced by an O H or an N H linkage. The works of Leszczynski35, and of the groups of Lapinski61, Parchment62 and Alhambra36 among others, clearly show the significant effects of second-order electron correlation effects on the stabilization of the thiol forms. In some particular cases there still remain significant discrepancies regarding the experimental energy differences between the different tautomers and the aforementioned theoretical estimations. This is particularly

1364 M. T. Molina, M. Ya´nez,˜ O. Mo,´ R. Notario and J.-L. M. Abboud

true for diazinethiones, where SCF C MBPT(2) calculations predict the thiol tautomer of pyridine-2-thiol to be 6.6 kcal mol 1 more stable than the thione one63, in clear contrast

with the experimental evidence which reduces this difference to 2.4 š 0.2 kcal mol 163 . This was taken as an indication that electron correlation effects beyond second order might be important, at least for this particular system. This was indeed ratified by a recent paper62 where it was shown that the thiol/thione energy difference decreases to 3.6 kcal mol 1 when evaluated at the QCISD(T) (Quadratic Configuration Interaction including single and double excitations and estimating the contribution of the triples to the energy in a perturbative way)64, which is practically correct to fifth order.

These results indicate that an accurate description of the energetics of the system would require what is usually called high level ab initio calculations, where the energy of the system is practically correct to fifth order and the basis set of a ‘near limit’ quality. No doubt such calculations are very expensive and only feasible for very small systems, which are not of interest when one is dealing with thiocarbonyl derivatives, where the parent compound, thioformaldehyde, has already 34 electrons. Pople and coworkers65 have developed a theoretical scheme, usually called Gaussian-2 (G2) theory, which provides total energies effectively at the quadratic configuration interaction QCISD(T)/6-311 C G(3df,2p) level, with a moderately large computational effort. G2 theory is in general accurate to š0.1 eV for dissociation energies, ionization potentials, electron affinities and proton affinities. This general procedure has been also applied with success to reproduce accurately heats of formation, which are obtained by substracting the atomization energies from known enthalpies of formation of the isolated atoms. In particular, the G2 heats of formation of thioformaldehyde and its cation are reported66 to be in good agreement with experimental data. Further examples shall be examined later.

It seems quite obvious that the evaluation of heats of formation requires unavoidably high level ab initio calculations, since high-order electron correlation effects are very important when breaking the different bonds of a molecule. Nevertheless, in thiocarbonyl chemistry there are examples of other processes, such as valence or thiol/thione tautomerisms, where these high level calculations are required to get results in agreement with experiment. An example of this discrepancy between experiment and calculations, when the latter are not carried out at a sufficiently high level of accuracy, is provided by 1,2-dithioglyoxal (2a) and its valence tautomer 1,2-dithiete (2b). There is experimental evidence from PES67, gas-phase microwave studies68 and low-temperature matrix IR spectroscopy69 which shows that 2b is more stable than 2a. Ab initio studies at different levels (see Table 4), including different basis sets and fourth-order correlation calculations, fail to predict the correct stability of 1,2-dithiete. Jonas and Frenking70 have shown that the correct stability order 2b > 2a is obtained only when a set of f functions is

TABLE 4. Relative energies (kcal mol 1) of 1,2- dithiete (2b) with respect to 1,2-dithioglyoxal (2a)