
- •Кинематика материальной точки
- •1. Механическое движение.
- •Скорость
- •Сравнение выражений (1.9) и (1.10) приводит к соотношениям
- •В математике выражение вида
- •Ускорение
- •Сопоставление этого выражения с (1.25) дает, что
- •Лекция 2 кинематика вращательного движения
- •Движение по криволинейной траектории
- •Поступательное движение твердого тела
- •Продифференцировав соотношение (2.6) по времени, получим
- •Лекция 3 Динамика материальной точки Инерциальные системы отсчета. Закон инерции.
- •Сила и масса.
- •Второй закон Ньютона
- •Единицы и размерности физических величин.
- •Третий закон Ньютона
- •Сила тяжести и вес
- •Упругие силы.
- •Силы трения.
- •Лекция 4 Сохраняющиеся величины.
- •Закон сохранения импульса
- •Энергия и работа.
- •Кинетическая энергия и работа.
- •Лекция 5 Консервативные силы
- •Потенциальная энергия материальной точки во внешнем силовом поле
- •Лекция 6 Потенциальная энергия взаимодействия
- •В случае гравитационного притяжения частиц
- •Нетрудно убедится в том, что в этом случае
- •В этой сумме имеется n(n-1) слагаемых (каждая из n частиц взаимодействует с n-1 частицей).
- •Закон сохранения энергии
- •Где определяется формулой (3.30).
- •Соударения тел
- •Лекция 7 Момент силы
- •Закон сохранения момента импульса
- •Плоское движение твердого тела
- •Вращение твердого тела вокруг неподвижной оси
- •Момент инерции
- •Кинетическая энергия вращающегося тела
- •Сумма энергий (Еk)I дает кинетическую энергию всего тела:
- •Кинетическая энергия тела при плоском движении
- •Возведение в квадрат дает
- •Лекция 9 Кинетическая энергия вращающегося тела
- •Сумма энергий (Еk)I дает кинетическую энергию всего тела:
- •Кинетическая энергия тела при плоском движении
- •Возведение в квадрат дает
- •Лекция 10 Механические колебания Колебательное движение, общие сведения о колебаниях
- •Малые колебания
- •Гармонические колебания
- •Введя обозначения
- •Затухающие колебания.
- •Применив обозначения
- •Маятник
- •2.5. Вынужденные колебания. Резонанс. Автоколебания
- •Лекция 11 Упругие волны Распространение волн в упругой среде
- •Уравнения плоской и сферической волн
- •Волновое уравнение
- •Стоячие волны
Движение по криволинейной траектории
При
равномерном движении по криволинейной
траектории
![]() =0,
так что скорость изменяется только по
направлению. Легко сообразить, что
направление скорости будет изменяться
тем быстрее, чем больше кривизна
траектории и чем быстрее движется
частица.
=0,
так что скорость изменяется только по
направлению. Легко сообразить, что
направление скорости будет изменяться
тем быстрее, чем больше кривизна
траектории и чем быстрее движется
частица.
Представив скорость в виде
v=vev (2.8)
(ev-орт скорости v), рассмотрим два частных случая; 1) движение по прямолинейной траектории и 2) равномерное движение по окружности.
При прямолинейном движении ev=const, изменяется только v, поэтому
а=![]() еv
(2.9)
еv
(2.9)
Из
этого выражения следует, что в случае,
когда скорость со временем увеличивается
(т.е.
![]() ),
ускорение направлено так же, как скорость,
а модуль ускорения равен
),
ускорение направлено так же, как скорость,
а модуль ускорения равен![]() .
Если же
скорость со временем уменьшается (т.е.
.
Если же
скорость со временем уменьшается (т.е.
![]() <0), направление ускорения противоположно
направлению скорости, а модуль ускорения
равен
<0), направление ускорения противоположно
направлению скорости, а модуль ускорения
равен
![]() (напомним, что модуль вектора должен
быть положительным).
(напомним, что модуль вектора должен
быть положительным).
При равномерном движении по окружности v=const, изменяется только еv, поэтому
а=v![]() .
(2.10)
.
(2.10)
Из рис.2.3 следует, что за время t орт скорости поворачивается на угол =vt/R и получает приращение еv. По определению производной
![]() .
(2.11)
.
(2.11)
При t0 будет стремиться к нулю и угол . Поэтому, заменив хорду АВ на рис.2.3 б соответствующей дугой, можно положить еv приближенно равным (напомним, что стороны треугольника ОА и ОВ равны единице). При t отношение хорды к дуге будет стремиться к единице.
П ринявеv,
можно написать, что еvnI,
где nI-единичный
вектор, имеющий такое же направление,
как и еv.
При предельном переходе этот единичный
вектор превращается в n
– орт нормали
к траектории в той точке, в которой была
частица в момент t.
Подставив полученное значение еv
в формулу (2.11) и приняв во внимание, что
=vt/R,
получим
ринявеv,
можно написать, что еvnI,
где nI-единичный
вектор, имеющий такое же направление,
как и еv.
При предельном переходе этот единичный
вектор превращается в n
– орт нормали
к траектории в той точке, в которой была
частица в момент t.
Подставив полученное значение еv
в формулу (2.11) и приняв во внимание, что
=vt/R,
получим
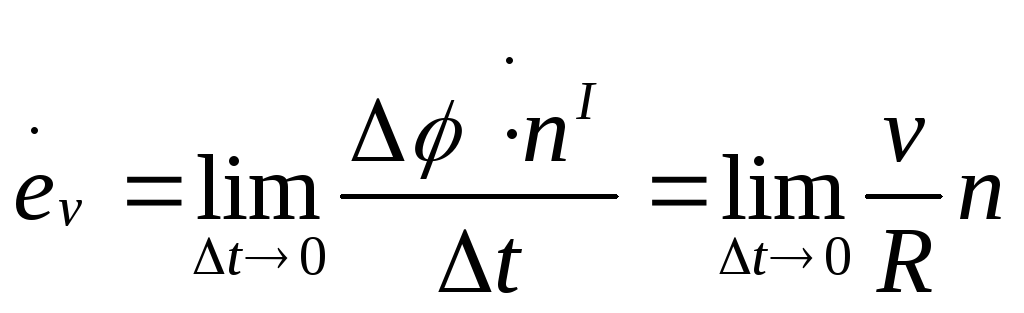 .
.
Как мы и предполагали, быстрота поворота вектора скорости (т.е. поворота еv) оказалась пропорциональной модулю скорости и кривизне траектории. (В случае окружности кривизна траектории характеризуется величиной, обратной радиусу.)
Подставив
найденное значение
![]() в формулу (2.9), получим, что
в формулу (2.9), получим, что
аn=![]()
![]() (2.12)
(2.12)
Таким образом, при равномерном движении по окружности ускорение определяется выражением (2.12). Направлено ускорение по нормали к скорости. Поэтому его называют нормальным ускорением и в обозначении его ставят индекс n.
Каждой точке произвольной искривленной линии можно сопоставить окружность, которая сливается с линией на бесконечно малом участке (рис.2.4).
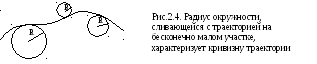
Радиус этой окружности характеризует кривизну линии в данной точке и называется радиусом кривизны.
Если частица движется равномерно по произвольной криволинейной траектории, ускорение также определяется формулой (2.12), причем под r подразумевается радиус кривизны траектории в той точке, где находится в данный момент частица.
При неравномерном движении частицы по криволинейной траектории оба множителя в формуле (2.8) изменяются со временем. Применив правило дифференцирования произведения двух функций, получим выражение
а=![]() ,
,
из которого следует, что в общем случае ускорение распадается на два слагаемых. Одно из них, как мы выяснили ранее, коллинеарно скорости и, следовательно направлено по касательной к траектории. Поэтому его называют тангенцальным (т.е. касательным) ускорением и обозначают а. Второе является нормальным ускорением.
Итак,
а=а+аn=![]() (2.13)
(2.13)
(обычно вместо еv пишут - орт касательной, однако мы предпочитаем писать еv, чтобы подчеркнуть, что это орт скорости). Первое слагаемое характеризует быстроту изменения модуля скорости. Второе слагаемое – быстроту изменения направления скорости.
Составляющие а и аn перпендикулярны друг к другу. Поэтому квадрат модуля ускорения равен сумме квадратов модулей составляющих
а=![]() .
(2.14)
.
(2.14)
