17 Работа и кинетическая энергия

1. Покажем теперь, что работа силы, действующей на тело, однозначно связана с изменением энергии этого тела.

Пусть на тело, движущееся в горизонтальной плоскости без трения, в течение некоторого времени действовала переменная сила, которая изменила скорость этого тела от до, причем во время движения тело не выходило из указанной горизонтальной плоскости (это ограничение означает, что высота тела над поверхностью Земли остается неизменной).

Выясним, на что затрачивается работа этой силы.

П

одсчитаем сначала работу, совершаемую силой на бесконечно малом отрезке пути(рис.22). Согласно (16.5) она равна, где(или) – касательная составляющая силы. Касательная составляющая силы сообщает телу тангенциальное ускорение. По второму закону Ньютона =m (в скалярном виде).

Мы знаем, что численное значение тангенциального ускорения равно производной от скорости по времени: =.

Тогда .

Но есть численное значение скорости в произвольный момент времениt. Следовательно,

. (17.1)

Чтобы найти полную работу, совершаемую силой на всем пути от точки 1 (начальное состояние) до точки 2 (конечное состояние), надо сложить все элементарные работы, т.е. проинтегрировать выражение (17.1).

.

Начальное состояние характеризуется скоростью , конечное -, поэтому пределы интегрирования 1-2 можно представить как

-- :

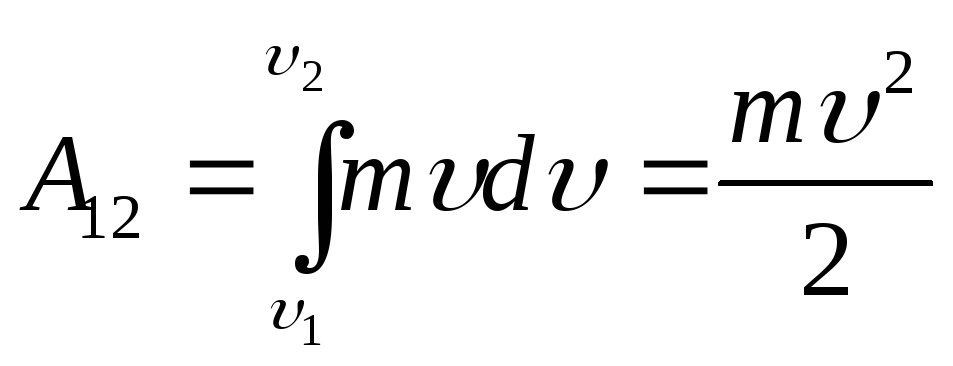
. (17.2)

Мы видим, что работа силы, изменяющей величину скорости тела равна разности двух значений физической величины , где С – некоторая произвольная постоянная. Величинаявляетсяфункцией состояния тела, так как ее изменение не зависит от пути перехода тела из начального состояния 1 в конечное состояние 2, от способов, посредством которых достигнуто изменение скорости от значения до значения. Иными словами, изменение этой величины не зависит от того, каковы были промежуточные состояния, быстро или медленно изменялась скорость тела, какая сила – постоянная или переменная – действовала на него, по какой траектории – прямолинейной или криволинейной – происходило движение и т.д. Если скорость тела массойизменилась отдо, то это значит, что силы, действующие на тело, совершили за это время работу, величина и знак которой определяются разностью. По изменению величиныможно судить о величине произведенной

работы и, наоборот, по совершенной работе можно судить об измене-нии величины .

Функцию механического состояния, зависящую от скорости движения тела, называют кинетической энергией:

=. (17.3)

Константа должна быть определена. Из физических соображений ясно, что кинетическая энергия равнанулю, если равна нулю скорость тела = 0. Отсюда следует, что= 0. Следовательно,

. (17.4)

Используя введенное обозначение, соотношение (17.2) можно переписать:

, (17.5)

где - кинетическая энергия тела в начальном состоянии;

- кинетическая энергия тела в конечном состоянии;

- работа, совершаемая силой, действующей на тело, в процессе перехода его из начального состояния в конечное.

Обозначим -=.

Тогда =. (17.6)

2. В общем случае изменение скорости тела может быть обусловлено совместным действием нескольких сил. В этом случае под в выражении (17.6) следует пониматьалгебраическую сумму работ, совершаемых всеми силами:

=. (17.7)

Если скорость изменяется на бесконечно малую величину, то

. (17.8)

Таким образом, приращение кинетической энергии тела при его переходе из одного состояния в другое равно алгебраической сумме работ, совершаемых всеми силами, действующими на него в процессе этого перехода. Это утверждение носит название теоремы об изменении кинетической энергии, а соотношения (17.6) и (17.8) есть матема-тические выражения (интегральное и дифференциальное) этой теоремы.

Из формулы (17.6) видно, что если работа силы, действующей на тело, положительна, то кинетическая энергия тела возрастает (> 0), тело получает энергию от тех тел, которые являются «источником» силы, если эта работаотрицательна, то энергия уменьшается (< 0), телоотдает энергию окружающим телам.

3. Обладая кинетической энергией, тело способно совершить работу, т.е. способно отдать эту энергию другим телам – заставить их двигаться, изменять скорость, деформироваться и т.д. В этом смысле говорят об энергии как о способности тела совершать работу. Максимум работы, которую может совершить тело в данной системе отсчета благодаря тому, что оно перемещается, обладает скоростью, определяется запасом его кинетической энергии, т.е. величиной .