
Математика практикум
.pdfМинистерство общего и профессионального образования Российской Федерации
Омский государственный институт сервиса Кафедра высшей математики и информатики
Н.В. Алексеенко, Р.И. Воробьева, О.П. Диденко, О.В. Кириченова
МАТЕМАТИКА
ПРАКТИКУМ
ОМСК 2001
4
Математика: Практикум/ / Н.В. Алексенко, Р.И. Воробьева, О.П. Диденко, О.В. Кириченова. Омский государственный институт сервиса, 2001г. – 108 с.
Данное издание предназначено для использования на практических занятиях и для самостоятельной работы студентов. В него включены задачи по всем основным разделам стандартного курса математики.
Практикум составлен с учетом государственного образовательного стандарта высшего профессионального образования и рабочих программ по курсу «Математика».
Практикум предназначен для студентов экономического и худо- жественно-технологического факультетов, изучающих математику.
Разделы 1, 2 составлены Н. В. Алексенко, разделы 3 - 6 – О.П.Диденко, разделы 7, 11 – О. В. Кириченовой, разделы 8 - 10 – Р.И.Воробьевой.
Библиогр.: 17 назв. Табл. 45. Рис. 15.
Рецензент к.т.н., доц. О.А. Попова Ответственный за выпуск зав. кафедрой ВМ и И О.А. Попова
Рекомендовано заседанием кафедры ВМ и И Протокол № 15 от 16.05.01 г.
Утверждено научно-методическим советом спец. 060500, протокол № 10 от 20.06.2001 г.; спец. 060800, протокол № 10 от 18.05.2001 г.
РАЗДЕЛ 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

5
Операции над матрицами
|
|
|
|
Свойства операций над матрицами |
|||
1. |
A |
B |
B |
A. |
|
5. |
(A B) A B . |
2. |
(A |
B) |
C A |
(B C) . |
6. |
. |
|
3. |
(A |
B)C |
AC |
BC. |
7. |
A(BC) (AB)C . |
|
4. A(B C) AB AC . |
|
|
|
8. |
АТ |
Т |
А . |
|
|||||||
1.1. Вычислить матрицу |
D |
(AB)Т |
C2 , где Т – знак транспони- |
||||||||||||
рования: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 4 2 |
|
|
|
2 |
0 |
|
|
|
1 |
3 |
|
|||
1) A |
, |
|
B 1 3 , |
C |
|
; |
|||||||||
|
|
|
|
||||||||||||
|
1 |
0 |
5 |
|
|
|
0 |
5 |
|
|
0 |
4 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 2 0 |
|
|
|
1 |
0 |
|
|
0 1 |
|
|
||||
2) A |
|
, |
B |
1 2 , |
C |
; |
|
||||||||
|
1 |
0 |
3 |
|
|
1 |
1 |
|
|
2 |
3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
0 |
|
|
|
3 4 2 |
|
|
1 |
1 |
0 |
|
|||
3) A 1 3 , |
|
B |
, |
C 0 0 2 ; |
|||||||||||
|
0 |
5 |
|
|
|
1 |
0 |
5 |
|
|
1 |
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
0 |
|
|
|
|
|
|
|
|
0 |
1 |
2 |
|
|
|
|
|
|
1 |
2 |
0 |
|
|
|
|
|
|
|||
4) A |
1 2 , B |
, C |
1 0 1 . |
||||||||||||
1 0 3 |
|||||||||||||||
|
1 |
1 |
|
|
|
|
|
|
|
|
1 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.2. Вычислить матрицу D = CАВ:
1 |
2 |
3 |
1 |
1) A 1 0 2 , |
B 2 , C 2 0 5 ; |
||
4 |
5 |
3 |
1 |

6
|
|
|
|
0 |
1 |
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2) A 1 3 1 , B |
|
5 , C 12 0 0 . |
|
|
|
|
|||||||||||||
|
|
|
|
3 |
4 |
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1.3. |
Даны |
|
матрицы |
|
А, |
В. |
|
|
Вычислить |
матрицу |
||||||||||
X A2 |
AB BA 3E , где |
Е - единичная матрица соответствующей |
||||||||||||||||||
размерности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
№ |
Матрица А |
|
Матрица В |
|
Матрица А |
Матрица В |
|
||||||||||||
|
|
|
3 |
|
1 |
0 |
|
1 0 |
0 |
|
3 |
|
1 |
1 |
3 |
0 |
0 |
|
||
|
1 |
|
2 |
0 1 |
|
0 3 |
0 |
6 |
0 |
2 –1 |
0 –3 0 |
|
||||||||
|
|
|
1 |
1 3 |
|
0 0 |
2 |
|
1 |
0 –2 |
0 |
0 1 |
|
|||||||
|
|
|
1 |
4 |
1 |
|
3 |
0 |
0 |
|
0 |
0 |
3 |
1 |
0 |
0 |
|
|||
|
2 |
|
2 |
1 |
0 |
|
0 |
5 |
0 |
7 |
1 |
2 |
1 |
0 |
1 |
0 |
|
|||
|
|
|
–1 |
0 0 |
|
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
2 |
|
||||
|
|
|
1 |
0 |
1 |
|
4 |
0 |
|
0 |
|
1 |
0 |
0 |
3 |
0 |
0 |
|
||
|
3 |
|
4 1 |
0 |
|
0 –1 0 |
8 |
0 |
3 |
4 |
0 |
5 |
0 |
|
||||||
|
|
|
2 |
0 |
1 |
|
0 |
0 |
|
2 |
|
0 |
1 |
5 |
0 |
0 |
1 |
|
||
|
|
|
2 |
|
1 |
1 |
|
5 |
0 |
|
0 |
|
2 |
|
5 |
0 |
4 |
0 |
0 |
|
|
4 |
|
–1 3 0 |
|
0 |
1 0 |
9 |
1 |
4 0 |
0 |
3 |
0 |
|
|||||||
|
|
|
0 |
1 –2 |
|
0 |
0 –2 |
|
0 |
0 –1 |
0 |
0 |
2 |
|
||||||
|
|
|
0 1 |
2 |
|
–1 0 0 |
|
2 |
1 |
0 |
1 |
0 |
0 |
|
||||||
|
5 |
|
3 |
|
0 |
1 |
|
0 2 |
0 |
10 |
0 |
2 |
0 |
0 |
2 |
0 |
|
|||
|
|
|
0 –1 –2 |
|
0 0 |
4 |
|
0 |
0 |
4 |
0 |
0 |
3 |
|
||||||
1.4. Вычислить А 3 :
1 |
1 |
|
1 |
|
1 |
0 |
0 |
|
|
|
|
|
|||
1) A 3 |
|
1 2 |
; |
2) A 0 |
2 |
0 . |
|
2 |
|
1 |
0 |
|
0 0 |
3 |
|
|
|
|
|
|
|||
1.5. Предприятие выпускает продукцию двух видов: P1 , P 2 и использует сырье трех типов: S1 , S2 , S3 . Нормы расхода сырья характеризуются матрицей A { i j} , где i j (i = 1,2; j = 1, 2, 3) – количество единиц сырья типа S j , необходимого для производства единицы продукции вида Pi . План выпуска продукции задан матрицейстрокой В. Стоимость единицы каждого типа сырья задана
|
|
|
|
|
7 |
|
|
|
|
матрицей-столбцом С. |
Определить затраты сырья, необходимые |
||||||||
для планового выпуска продукции, и общую стоимость сырья. |
|||||||||
|
№ |
Матрица |
|
А |
Матрица В |
Матрица С |
|
||
|
|
1 |
2 |
3 |
|
|
|
10 |
|
|
1 |
|
100 |
150 |
20 |
|
|||
|
4 |
0 |
5 |
|
|
||||
|
|
|
|
|
10 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
|
|
|
10 |
|
|
2 |
|
50 |
100 |
10 |
|
|||
|
1 |
1 |
0 |
|
|
||||
|
|
|
|
|
10 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
0 |
|
|
|
10 |
|
|
3 |
|
200 |
100 |
20 |
|
|||
|
1 |
0 |
1 |
|
|
||||
|
|
|
|
|
30 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
20 |
|
|
4 |
|
100 |
100 |
10 |
|
|||
|
1 |
2 |
4 |
|
|
||||
|
|
|
|
|
10 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
10 |
|
|
5 |
|
150 |
100 |
10 |
|
|||
|
0 |
1 |
1 |
|
|
||||
|
|
|
|
|
10 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
4 |
|
|
|
10 |
|
|
6 |
|
100 |
200 |
10 |
|
|||
|
1 |
1 |
2 |
|
|
||||
|
|
|
|
|
10 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
40 |
|
|
7 |
|
100 |
150 |
10 |
|
|||
|
2 |
3 |
0 |
|
|
||||
|
|
|
|
|
10 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
5 |
0 |
|
|
|
10 |
|
|
8 |
|
100 |
50 |
10 |
|
|||
|
1 |
0 |
4 |
|
|
||||
|
|
|
|
|
22 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0 |
1 |
|
|
|
30 |
|
|
9 |
|
50 |
50 |
10 |
|
|||
|
0 |
3 |
1 |
|
|
||||
|
|
|
|
|
20 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
0 |
|
|
|
5 |
|
|
10 |
|
200 |
300 |
10 |
|
|||
|
3 |
2 |
1 |
|
|
||||
|
|
|
|
|
20 |
|
|||
|
|
|
|
|
|
|
|
|
|
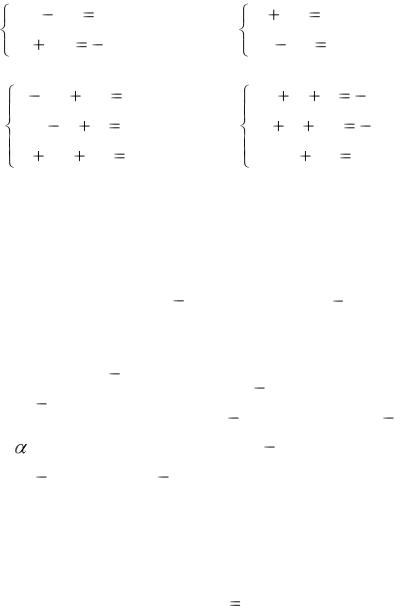
1.6. Записать в матричной форме системы уравнений, пользуясь понятием произведения и равенства матриц:
|
|
|
|
|
|
8 |
|
|
|
1) |
2x |
3y |
1, |
|
2) |
y |
4z |
0, |
|
3x |
4 y |
2; |
|
2 y |
3z |
1; |
|
||
|
|
|
|
||||||
|
x |
4 y |
2z |
11, |
|
x |
y |
z |
2, |
3) 2x |
y |
z |
9, |
4) 3x |
y |
4z |
13, |
||
|
x 2 y 3z 7; |
|
|
9 y 5z 5. |
|||||
Определители и их свойства
1.7. Вычислить определители 2-го и 3-го порядков:
|
|
1 |
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Sinx |
|
|
|
|
|
|
|
|
|
|||||||
1) |
; |
|
|
|
|
2) |
|
|
|
; |
|
|
3) |
Cosx |
|
|
; |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
2 |
4 |
|
|
|
|
|
|
|
|
3 0 |
|
|
|
|
|
Sinx |
|
Cosx |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4) |
|
11 |
9 |
|
; 5) |
|
123 |
0 |
|
; |
6) |
|
1 |
2 |
|
|
3 |
|
; 7) |
|
2 |
2 |
|
1 |
|
; |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
1 |
|
2 |
|
|
3 |
1 |
|
2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
0 |
2 |
|
|
|
|
10 |
|
1 |
|
|
|
|
|
|
1 |
2 |
|
2 |
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
3 |
|
|
|
|
1 |
|
0 |
|
|
0 |
|
|
|
2 |
10 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
8) |
|
b |
1 |
|
2 |
; 9) |
0 |
|
3 |
0 |
; 10) |
0 |
|
1 |
|
0 |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
c |
3 |
|
1 |
|
|
|
|
0 |
|
0 |
|
|
4 |
|
|
|
0 |
|
0 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1.8. Доказать, что определитель диагональной матрицы равен |
||||||||||||||||||||||||||||||||||||||||||
произведению |
элементов главной диагонали. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
1.9. Решить уравнение |
det A |
0 для заданной матрицы A. |
|
|
||||||||||||||||||||||||||||||||||||||
|
№ |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|||||
|
Матрица |
|
|
х |
3 |
|
|
|
2–х |
|
1 |
|
1 х х |
|
3–х 1 |
6 |
|
|
1–х 0 2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
х 1 х |
|
|
|
3 2–х 6 |
|
|
|
1 1–х –1 |
|||||||||||||||||||||||||||
|
A |
|
|
|
3 |
х |
|
2 |
|
3–х |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
х х –2 |
–9 –2 –7–х |
|
|
|
0 0 2–х |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1.10. Найти миноры и алгебраические дополнения всех элементов |
||||||||||||||||||||||||||||||||||||||||||
матрицы В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
№ |
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 –1 |
2 |
|
1 0 |
|
|
2 |
1 |
3 4 |
|
|
0 1 2 |
1 |
|
|||||||||||
|
Матрица |
|
1 |
|
2 |
|
|
–1 |
|
0 |
|
|
|
|
|
1 |
3 |
4 2 |
|
1 1 1 0 |
|
||||||||||||||||||||||
|
В |
|
|
|
|
3 – 4 |
5 7 |
|
|
2 |
3 |
|
1 |
–1 |
3 4 |
|
3 4 2 1 |
2 3 4 1 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
4 –2 |
3 |
1 –1 1 |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
1 3 |
|
|
1 |
0 0 |
1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
9
1.11. Вычислить определители следующих матриц разложением по элементам целесообразно выбранной строки (столбца).
№ |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
1 |
0 |
3 1 |
2 |
3 –1 1 |
1 2 2 0 |
4 |
6 –2 |
4 |
|||||||
Матрица |
0 |
1 –1 2 |
1 |
0 –1 |
2 |
–1 0 1 –3 |
1 2 –3 1 |
|||||||||
2 –1 |
1 0 |
0 –3 0 |
1 |
0 |
0 –2 |
1 |
4 –2 |
1 |
0 |
|||||||
|
||||||||||||||||
|
–1 |
0 |
1 4 |
1 |
2 |
3 |
0 |
0 |
3 |
1 |
1 |
6 |
4 |
4 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.12. Вычислить определитель матрицы двумя способами - разложением по первой строке и последнему столбцу.
№ |
|
1 |
|
|
2 |
3 |
|
4 |
|
|
5 |
|
||
|
1 0 |
2 |
0 |
–1 0 –2 0 |
2 1 0 0 |
0 0 1 2 |
1 |
2 |
0 |
0 |
||||
Матрица |
3 1 |
0 |
3 |
1 –3 0 0 |
1 0 3 1 |
1 1 –2 1 |
3 –1 1 2 |
|||||||
5 0 –2 –1 |
2 1 1 –1 |
2 2 4 –2 |
3 0 2 0 |
1 |
4 –2 0 |
|||||||||
|
||||||||||||||
|
1 1 |
4 |
0 |
3 2 4 2 |
1 –1 0 0 |
0 1 –1 0 |
5 |
0 |
0 |
1 |
||||
№ |
|
6 |
|
|
7 |
8 |
|
9 |
|
10 |
|
|||
|
3 1 |
0 0 |
2 0 |
9 1 |
1 –1 0 0 |
0 |
0 –1 1 |
0 |
2 |
0 –1 |
||||
Матрица |
–2 –1 3 0 |
1 4 |
0 0 |
2 –2 5 1 |
3 |
1 |
2 0 |
3 |
0 –1 2 |
|||||
1 4 |
0 1 |
–1 3 2 0 |
–1 0 3 2 |
0 –2 |
1 0 |
5 |
1 |
0 |
0 |
|||||
|
||||||||||||||
|
0 0 |
1 2 |
5 1 |
0 –2 |
4 1 0 0 |
5 |
0 |
0 3 |
0 –1 –2 0 |
|||||
Обратная матрица. Ранг матрицы
1.13. Найти обратные матрицы для следующих матриц.
№ |
1 |
|
2 |
|
|
3 |
|
4 |
|
5 |
|
|
Матрица |
1 |
2 |
3 |
4 |
Cosx |
–Sinx |
1 |
2 |
0 |
|
2 |
|
3 |
4 |
5 |
7 |
Sinx |
Cosx |
–1 0 |
3 –4 |
|||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
№ |
7 |
|
8 |
|
|
9 |
10 |
|
11 |
|
||
Матрица |
–1 |
1 |
2 5 |
7 |
–3 2 4 |
1 |
2 –1 |
1 |
2 |
3 |
||
6 3 |
4 |
2 1 0 |
4 |
7 –2 |
0 |
1 |
2 |
|||||
|
2 |
5 |
||||||||||
|
5 –2 –2 |
1 0 1 |
2 |
3 0 |
0 |
0 |
1 |
|||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
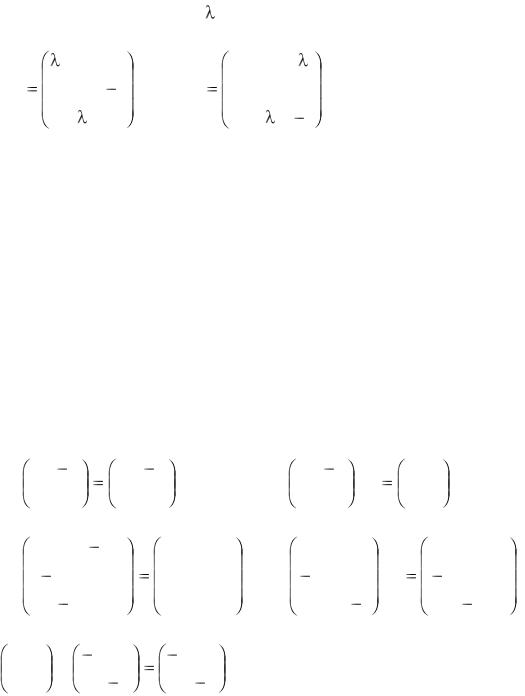
10
|
№ |
|
|
|
|
13 |
|
|
14 |
|
|
|
15 |
|
|
|
|
|
|
16 |
|
|
|
17 |
|
|
|
||
|
|
|
|
|
3 2 1 |
|
1 –2 3 |
|
|
4 |
7 |
0 |
0 |
|
|
|
1 |
1 |
1 |
1 |
1 2 3 4 |
|
|
||||||
|
|
|
|
|
|
|
|
1 2 0 0 |
|
1 1 –1 –1 |
0 1 2 3 |
|
|
||||||||||||||||
|
Матрица |
|
2 3 1 |
|
2 |
3 –4 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
0 0 7 –4 |
1 –1 1 –1 |
0 0 1 2 |
|
|
||||||||||||||||||||
|
|
|
|
|
2 1 3 |
|
3 –2 –5 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
0 0 5 –3 |
1 –1 –1 1 |
0 0 0 1 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1.14. При каких значениях |
|
матрица А не имеет обратной: |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
4 |
1 |
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) A 2 5 |
|
1 ; 2) A 0 1 5 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
0 |
1 |
|
|
|
|
2 |
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
1.15. Определить ранг матрицы В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ |
|
|
|
|
1 |
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 0 3 |
|
5 1 |
0 2 –1 3 |
|
|
|||||||
|
Мат- |
|
|
2 |
5 6 |
1 2 1 4 |
|
|
1 3 7 |
2 5 |
|
|
5 3–3 –1 |
|
|
||||||||||||||
|
|
|
|
|
|
4 3 1 |
|
7 5 |
|
||||||||||||||||||||
|
рица |
|
|
|
4 –1 5 |
|
0 5–1 4 |
|
–1 0 4 |
8 3 |
|
|
–1 0 1 0 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
0 3 –5 –3 3 |
|
||||||||||||||||||||
|
В |
|
|
2 –6 –1 |
–1 3 4 6 |
3 6 10 –4 7 |
|
|
1 1 3 4 |
|
|
||||||||||||||||||
|
|
|
|
|
2 3 –2 |
|
|
2 4 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 6 0 6 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Системы линейных уравнений |
|
|
|
|
|
|
|
|||||||||||||||
|
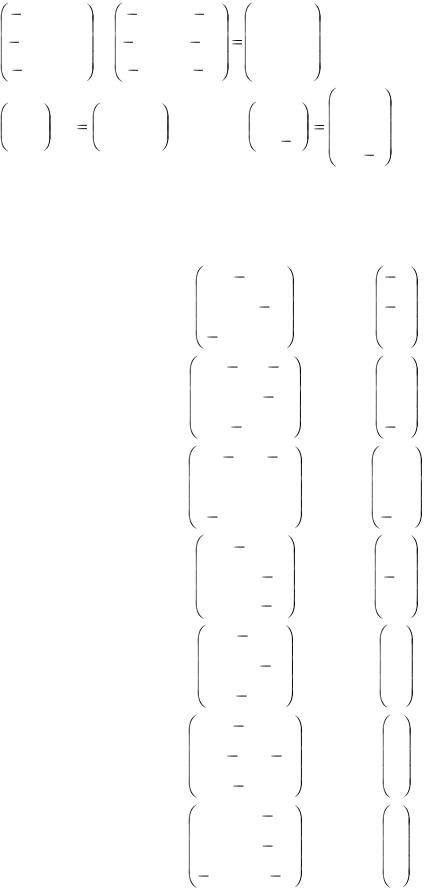
1.16. Решить матричное уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1) X |
3 |
2 |
2 |
4 |
; |
|
|
|
2) |
|
4 |
|
6 |
X |
|
2 5 |
; |
|
|
|
||||||||
|
|
|
|
5 |
4 |
6 |
8 |
|
|
|
|
|
|
2 |
1 |
|
|
|
|
1 |
3 |
|
|
|
|
||||
|
|
|
|
5 |
9 |
10 |
42 |
|
|
0 |
0 |
|
|
1 |
2 |
|
3 |
|
|
|
7 |
5 |
7 |
|
|
||||
|
3) X |
|
|
3 3 6 |
0 42 0 ; 4) |
|
|
1 1 2 X |
2 2 1 ; |
||||||||||||||||||||
|
|
|
|
7 |
21 |
28 |
0 |
0 |
42 |
|
|
3 |
|
2 |
|
1 |
|
|
11 |
1 |
7 |
|
|
||||||
5) |
2 |
1 |
X |
3 2 |
|
2 |
4 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
|
2 |
5 |
3 |
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
1 |
2 |
3 |
|
2 |
5 |
7 |
1 |
0 |
0 |
|
|
6) |
|
2 |
3 4 X 4 9 |
10 |
0 |
1 0 |
; |
|
|||||
|
|
1 |
1 |
2 |
|
1 |
2 |
2 |
0 |
0 |
1 |
|
|
|
2 |
|
1 |
|
1 0 7 |
|
4 3 |
|
2 |
8 |
|||
7) |
|
X |
; 8) X |
|
1 1 . |
||||||||
|
1 |
1 |
|
8 |
1 |
2 |
|
1 |
1 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
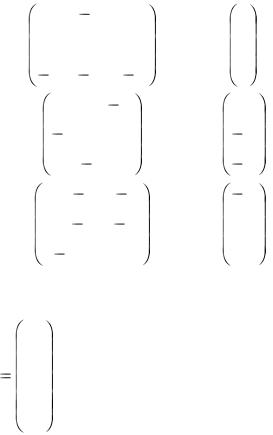
1.17. Доказать, что система линейных уравнений АХ = В имеет единственное решение и найти его матричным методом, по формулам Крамера и методом Гаусса.
№ |
|
А |
|
В |
|
4 |
2 |
3 |
5 |
1 |
3 |
1 |
2 |
8 |
|
1 |
5 |
2 |
4 |
|
|
|
|
|
|
5 |
1 |
3 |
2 |
2 |
2 |
3 |
1 |
4 |
|
1 |
2 |
3 |
5 |
|
|
|
|
|
|
1 |
2 |
4 |
9 |
3 |
2 |
3 |
1 |
2 |
|
3 |
1 |
5 |
15 |
|
|
|
|
|
|
4 |
5 |
7 |
6 |
4 |
3 |
2 |
9 |
4 |
|
1 |
2 |
3 |
0 |
|
|
|
|
|
|
2 |
1 |
1 |
7 |
5 |
1 |
1 |
1 |
2 |
|
2 |
1 |
3 |
11 |
|
|
|
|
|
|
1 |
1 |
3 |
0 |
6 |
2 |
2 |
1 |
7 |
|
3 |
2 |
5 |
0 |
|
|
|
|
|
|
2 |
5 |
8 |
8 |
7 |
4 |
3 |
9 |
9 |
|
2 |
3 |
5 |
7 |
|
|
|
|
|
12
|
1 |
3 |
5 |
3 |
8 |
7 |
3 |
2 |
3 |
|
1 |
2 |
3 |
9 |
|
|
|
|
|
|
2 |
5 |
7 |
4 |
9 |
3 |
4 |
2 |
9 |
|
4 |
7 |
9 |
8 |
|
|
|
|
|
|
4 |
3 |
2 |
9 |
10 |
1 |
3 |
5 |
0 |
|
3 |
2 |
1 |
7 |
|
|
|
|
|
1.18. Найти множество решений однородной системы АХ = 0,где x1
Xx2 , 0 - нулевой вектор.
x3
x4
№. |
|
А |
|
№ |
|
А |
|
|
|
3 –8 –7 –1 |
|
3 –1 2 1 |
|||||
1 |
–1 |
7 –5 –1,5 |
2 |
–4 |
5 –3 –1 |
|||
|
1 |
6 –3 |
5 |
|
2 |
3 |
1 |
3 |
|
3 –1 4 2 |
|
–1 –3 1 –8 |
|||||
3 |
–1 –2 –7 –1 |
4 |
2 –4 5 –12 |
|||||
|
5 –4 –1 |
3 |
|
4 |
2 |
3 2 |
||
|
1 8 –6 –2 |
|
2 1 –4 |
2 |
||||
5 |
–2 –3 1 –1 |
6 |
4 –9 2 |
4 |
||||
|
–3 –2 –4 –4 |
|
–1 5 –3 –1 |
|||||
|
3 |
1 1 –3 |
|
2 –4 –1 1 |
||||
7 |
1 |
3 –2 2 |
8 |
1 –7 –6 –3 |
||||
|
5 |
7 –3 1 |
|
–3 1 –4 –5 |
||||
|
|
|
|
|
|
|
|
|
1.19. Методом Гаусса найти общее решение и фундаментальную систему решений для следующих систем уравнений:
