Решение задач из файла «Постановка задач. Пояснения»

Задача 1. Предполагается, что ссуда размером 5000 тыс. рублей погашается ежемесячными платежами по 141,7 тыс. рублей. Рассчитать, через сколько лет произойдет погашение, если годовая ставка процента – 16% (функция КПЕР()). При помощи инструмента Таблица подстановки проанализировать зависимость срока погашения от процентной ставки (10%, 15%, 20%, 25%) и значения платежей (100, 120, 140, 160 и 180 тыс. рублей). Первая часть задачи решается следующим методом:

Рисунок 2. Формула для решения задачи

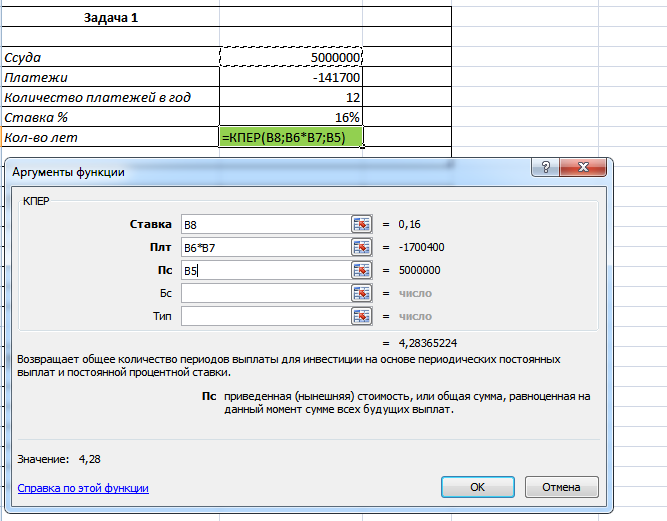
В аргументе «ПЛТ» умножаем ежемесячный платеж на 12, так мы получаем ежегодный платеж, поскольку процентная ставка у нас указана годовая, а не ежемесячная.

Теперь решение второй части задачи (создание таблицы подстановки)

Метод создания таблицы уже был указан выше, поэтому лишь обращу внимание, что адреса на эти аргументы «Подставлять значения по столбцам» и «Подставлять значения по строкам» нужно брать только с условия задачи, иначе таблицу просто не получится создать.

Рисунок 3. Создание таблицы подстановки 1

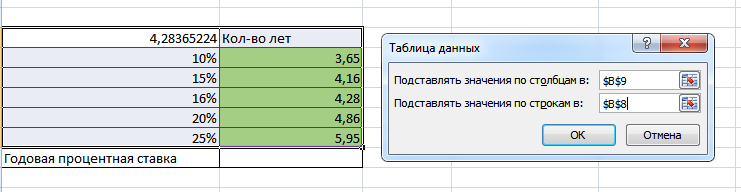
Рисунок 4. Создание таблицы подстановки 2

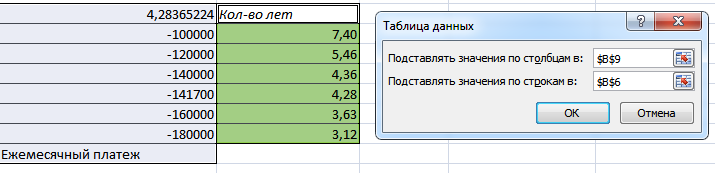
Задача решена, ответ найден, таблицы выведены. Переходим к следующей задаче

Задача 2. Существует два варианта денежных вкладов по 50 тыс. руб. в течение трех лет: в начале каждого года под 19% годовых или в конце каждого года под 27% годовых. Определить наиболее предпочтительный вариант (функция БС(), изменяется аргумент ТИП).

Рисунок 5. Формула для решения задачи

Сначала разбираемся с 1-ым вариантом – где проценты начисляются в начале года. Самое главное в этой функции – значение Тип, здесь мы его ставим на уровень 1, так как проценты начисляются в начале года. Конечная сумма указана ниже на рисунке. Теперь переходим ко 2-му варианту – с начислением процентов в конце года. Процесс такой же, как выше, только лишь с той разницей, что в аргументе Тип мы уже выставляем значение 0 или же оставляем его пустым. В итоге мы видим, что вклад с меньшей процентной ставкой оказался более выгодным, поскольку проценты начислялись в начале каждого года.

Задача 3. Ежегодная плата за приобретенную недвижимость на следующие 25 лет составляет 25 000 рублей. Если считать покупку недвижимости займом с 8% годовых, то какой должна быть его величина, чтобы рассчитаться с займом через 25 лет. (функция ПС())

Рисунок 6. Формула для решения задачи

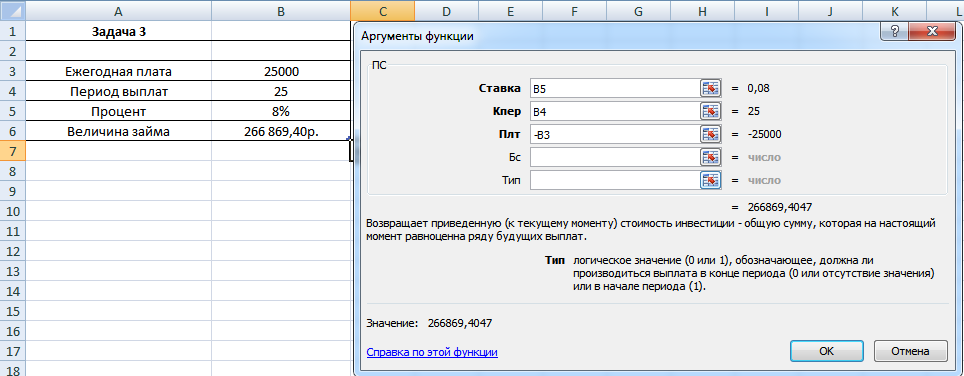
Как видно на рисунке – процесс решения не вызывает сложностей. Открываем функцию ПС, в аргументы проставляем соответствующие значения, и ответ готов.

Задача 4. Рассчитать будущую стоимость облигации номиналом 100 тыс. руб., выпущенной на 4 года, если предусмотрен следующий порядок начисления процентов: в первый год – 12,5%, в следующие два года – 14%, в последний год – 17% годовых БЗРАСПИС (первичное; план).

Рисунок 7. Формула для решения задачи

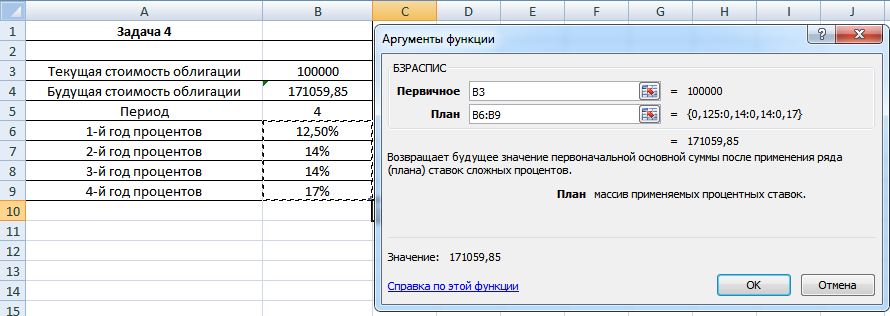
Процесс решения данной задачи также несложен и наглядно виден на изображении.

Задача 5. Ожидается, что будущая стоимость инвестиции размером 150 тыс. руб. к концу четвертого года составит 300 тыс. руб. При этом за первый год доходность составит 15%, за второй – 17%, за четвертый – 23%. Рассчитать доходность инвестиции за третий год, используя аппарат подбора параметра к функции БЗРАСПИС (первичное; план).

Рисунок 8. Формула для решения задачи

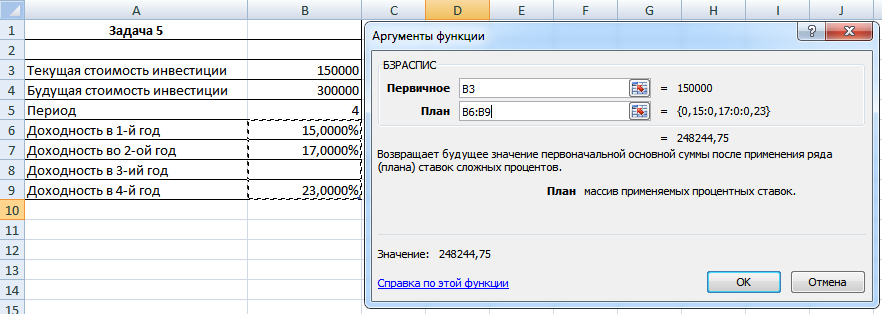
Несмотря на отсутствие значения процентной ставки за 3-ий год – также выделяем все 4 года начисления процентов (пусть 3-ий и отмечен как ноль), делается это в отдельную ячейку. Получится значение, меньшее, чем необходимые нам 300 тысяч, но к указанному значению нам поможет средство под названием Подбор параметра. Находится он там же, где и Таблица подстановки. Мы его запускаем, и видим примерно следующее:

Рисунок 9. Подбор параметра

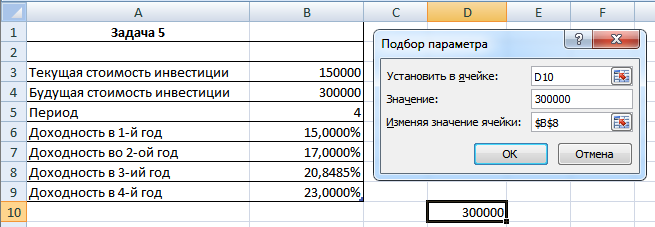
Теперь в этой отдельной ячейке мы должны установить значение в 300 тысяч путем наиболее точного подбора ставки процента на 3-ий год. Здесь указан уже готовый ответ, а поэтому во время подбора нажимаем на пустую ячейку с процентами на 3-ий год, что приведет к подбору точной ставки процента на этот год. Задача решена.

Задача 6. Облигации приобретены 01.07.96 по курсу 79,123 и имеют купонный доход в размере 12%, который выплачивается с периодичностью один раз в год. Предполагаемая дата погашения – 31.12.97 по курсу 100. Определить годовую ставку помещения. Рассчитать аргумент Доход, используя аппарат подбора параметра к функции Цена().

Рисунок 10. Формула для решения задачи

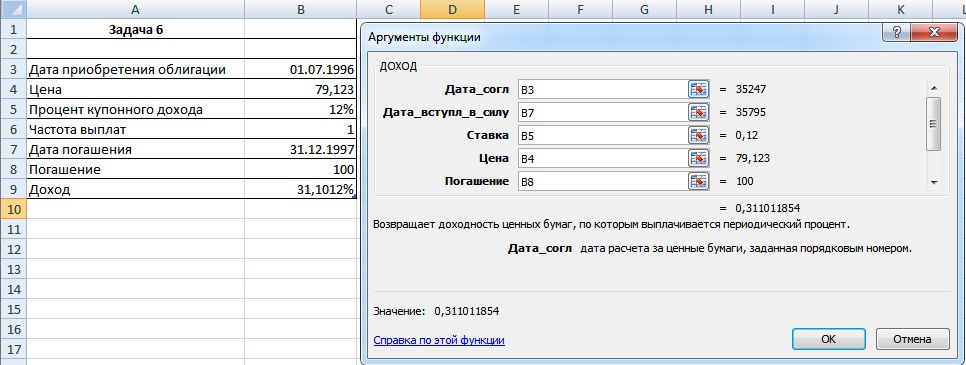
Вышеупомянутый аппарат подбора параметра использовать необязательно, так как и без него можно рассчитать Доход следующим образом: открываем функция Доход, в аргументы ставим соответствующие значения (там ниже в функции указана еще и Частота выплат), и получается ответ, указанный в десятичной дроби (нужно конвертировать в проценты). Задача решена.

Задача 7. Дать заключение по инвестиционному проекту для 5-ти регионов, используя средство Таблица подстановки, если известно, что:

• проект рассчитан на 5 лет;

• ставка дисконтирования по 1-му региону составляет 5%, по 2-му – 6%, по 3-му – 7%, по 4-му – 8%, по 5-му – 9%.

Другие данные о проекте приведены в таблице.

Таблица 1. Значения для расчетов

Год	Доходы	Расходы	Итого за год
1	100	800	-700
2	300	400	-100
3	500	300	200
4	700	-	700
5	800	-	800

Рассчитывается с помощью функции ЧПС().

Рисунок 11. Формула для решения задачи

Поскольку значения для всех 5 регионов одинаковы, за исключением процентных ставок, то и формулы для расчета будут идентичные. В аргумент Ставка указываем ячейку со значением процента, а в аргумент Значение1 массив значений Итого за год за все 5 лет этого проекта. Для первого региона это значение равняется 618,11; для вычисления остальных достаточно лишь расширить данную формулу на соответствующие ячейки для других регионов.

Задача 8. Для приобретения квартиры молодая семья планирует в дополнение к собственным накоплениям в размере $12 000 взять в банке ипотечный кредит сроком на 20 лет под 11,5% годовых. Ежемесячно семья может выплачивать по кредиту не более $700.

На какой кредит может рассчитывать семья? (Функция ПС()) Какой может быть стоимость приобретаемой квартиры?

Какой может быть стоимость приобретаемой квартиры, если взять в банке кредит с другими условиями: а) на 10 лет под 10,5% годовых; б) на 15 лет под 11% годовых?

Используя команду Таблица подстановки, рассчитать возможную стоимость приобретаемой квартиры: а) при различных размерах собственных накоплений и разных сроках действия кредита; б) при различных ежемесячных платежах по кредиту и разных сроках его действия.

Рисунок 12. Формула для решения задачи

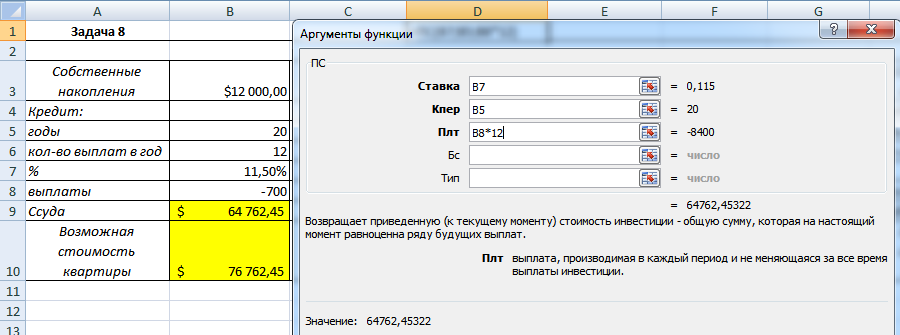
Сначала рассчитываем сумму кредита, на которую может рассчитывать семья. Возможная стоимость квартиры рассчитывается просто – необходимо сложить сумму сбережений и максимальный размер кредита.

Условие А (на 10 лет под 10,5% годовых)

Рисунок 13. Формула для решения задачи

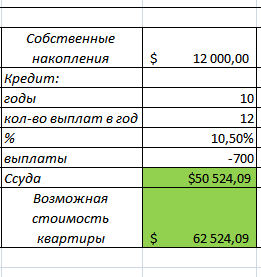
Процесс вычисления тот же самый, разница лишь в годовой ставке процента и периоде погашения кредита. То же самое и про условие Б (на 15 лет под 11% годовых)

Рисунок 14. Формула для решения задачи

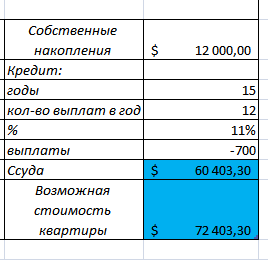
Теперь про таблицы подстановки, которых здесь нужно создать сразу две.

Условие 1 - при различных размерах собственных накоплений и разных сроках действия кредита

Рисунок 15. Таблица подстановки А

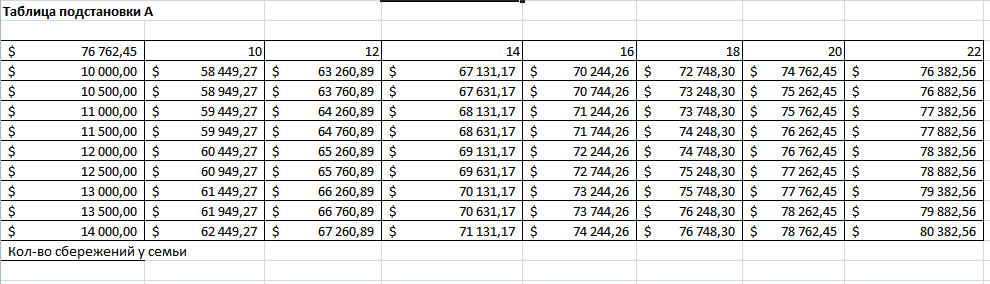
Процесс его создания уже был указан в начале, поэтому лишь напомню, что в верхнем левом углу должно стоять не просто значение, а формула, при помощи которой это значение выводится.

Теперь про условие 2 - при различных ежемесячных платежах по кредиту и разных сроках его действия

Рисунок 16. Таблица подстановки Б

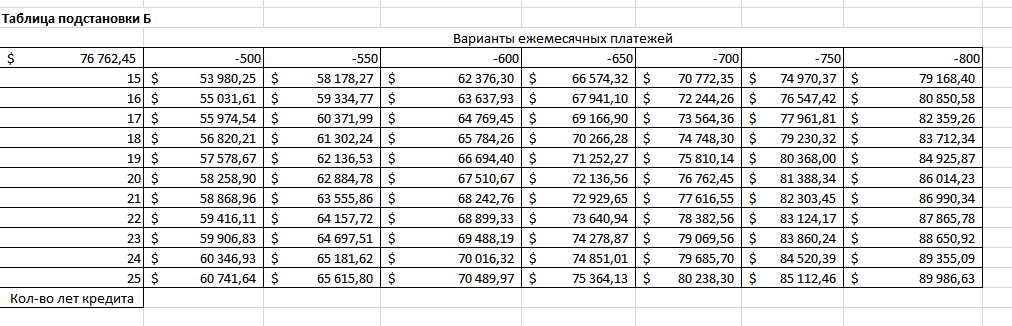
Никакой разницы в создании таблицы, а поэтому повторяться уже не имеет смысла.

Задача 9. Облигации номиналом 1000 рублей с купонной ставкой 12%, периодичностью выплат один раз в год выпущены 01.07.96. Дата первой оплаты купонов – 01.07.97, базис расчетов -1. Облигация приобретена 15.11.96 (дата соглашения). Определить накопленный купонный доход. (Функция НАКОПДОХОД())

Рисунок 17. Формула для решения задачи

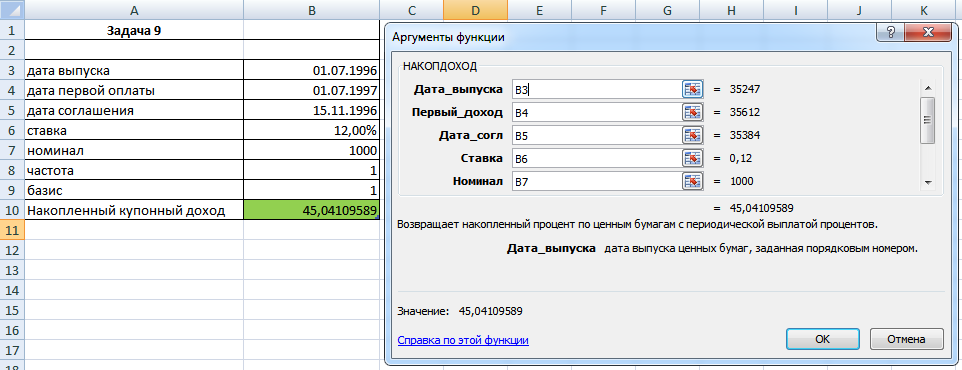
К сожалению – данная функция не помещается в один список, поэтому лишь поясню, что метод и функция решения мало чем отличаются от указанной в задаче 6, существенная разница лишь в использовании другой функции под названием НАКОПДОХОД.

Задача 10. У Вас на депозитном счету 10 570,5 рублей, положенные под 1% ежемесячно. Счет открыт 12 месяцев назад. Каков был начальный вклад? (Функция ПС())

Рисунок 18. Формула для решения задачи

Заострять внимание на уже решенных с подобной функцией задачах не будем, поэтому сразу перейдем к следующей задаче

Задача 11. Если использовать учетную ставку 0,75% в месяц, сколько необходимо выплатить вначале за имущество, которое по оценке будет стоить 5 000 000 рублей? Ежемесячная плата составляет 25 000 рублей в течение пяти лет. (Функция ПС())

Рисунок 19. Формула для решения задачи

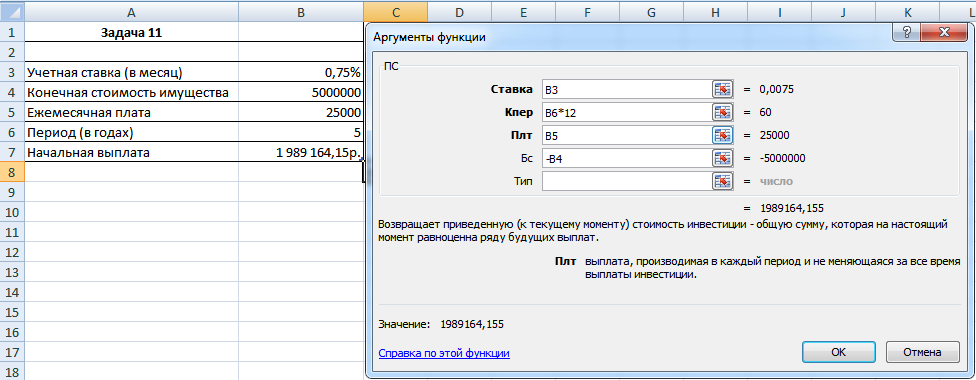
Здесь решено было умножить кол-во лет на 12, чтобы в формуле указывалось кол-во месяцев.

Задача 12. Вы можете позволить себе ежемесячные выплаты 2 500 рублей со ставкой 0,45% (в месяц) в течение 20 лет. Сколько можно занять, чтобы полностью погасить заем? (Функция ПС())

Рисунок 20. Формула для решения задачи

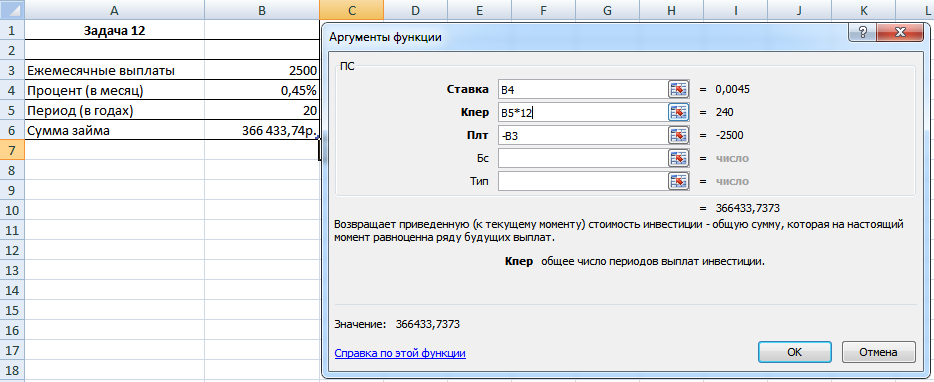
Случай абсолютно идентичный предыдущей задаче. Также умножаем кол-во лет на 12, чтобы получить кол-во месяцев.

И теперь переходим к последней задаче

Задача 13. Определить, какой из двух представленных проектов является наиболее привлекательным для инвестора. Ставка банковского процента составляет 13% годовых. Другие данные о проектах приведены в таблице. Рассчитывается с помощью функции ЧПС().

Таблица 2. Значения для расчетов

Рисунок 21. Формула для решения задачи

В аргумент Ставка мы указываем процент, а в аргумент Значение1 мы выставляем массив доходов. Подсчитав их сумму, теперь необходимо из них вычесть сумму инвестиций для нахождения уровня прибыли. То же самое проделываем и со вторым проектом, после – сравниваем. И как видно из рисунка – первый проект оказался выгоднее второго.