
Волны / Неуважев В.Е. Математическое моделирование турбулентного перемешивания (2000)
.pdf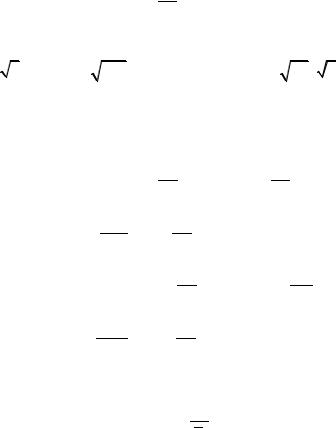
Как и раньше, рассмотрим сперва уравнение для плотности смеси (2.1), которое с учетом допущения (8.4) перейдет в следующее:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ ρ |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∂ |
|
|
ρ |
|
|
|
, |
|
|
|
при |
|
|
|
|
x> |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ τ |
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ ρ |
|
|
|
|
|
|
|
|
|
∂ |
|
2ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
x< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8.5) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при |
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ τ |
2 ∂ |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ τ= |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cµ |
|
∂ |
|
|
|
t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Эти уравнения совпадают с ранее полученными (7.32). Определение |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
эффективной ширины остается прежним [см. (7.2)]: |
|
|
|
|
|
|
|
|
|
β 2 ) |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
L1 = 2η 1 τ; |
|
|
L2= |
|
|
|
2η1 |
|
|
|
|
β 2τ ; L= |
L+ 1 |
|
|
|
|
=L2 |
|
|
|
2η+1 (1 |
|
|
τ . |
(8.6) |
||||||||||||||||||||||||||||||||||||||||||||||
Прежде чем провести осреднение уравнений (8.1) и (8.2) разделим их |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
на коэффициент диффузии Dε + |
. Аналогично мы поступали в §7 для k– |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
модели. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Перейдем к эйлеровым координатам и получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
∂ ρ k |
+ ρ |
ε t |
|
|
|
|
= |
|
|
|
g |
Dε |
∂ |
ρ + |
|
|
|
|
|
α 8 ∂ |
|
|
|
|
ρ D∂ |
+k |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
∂ τ |
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
∂ x D ∂ |
|
|
|
|
|
|
|
|
|
|
|
ε |
x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ∂ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
ε + |
|
|
|
|
|
|
|
|
|
|
|
ε+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
D |
|
|
|
|
∂ ln ρ |
|
|
∂ ρ k |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
∂ lnρ |
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||
+ |
|
|
|
|
|
|
|
|
+ |
|
|
|
∂ ρ |
− |
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂ x |
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
D |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
x 3 |
|
|
∂ |
|
|
τ |
|
|
|
D |
+ |
|
|
∂ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8.7) |
||||||
|
∂ ρε |
|
|
|
|
|
|
|
c ρε |
|
|
|
2 |
|
|
|
|
|
cµ cε 1k |
|
|
∂ ρ α |
|
|
|
|
|
|
∂ |
|
ε ∂ |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
8 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
+ |
|
|
|
|
ε 2 |
|
|
|
|
t |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
ρ |
D |
|
|
|
|
+t |
|
|
|||||||||||||||||
|
|
∂ τ |
|
|
|
kD |
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
∂ |
|
|
|
|
|
|
|
|
∂ |
x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x D |
|
|
ε∂ |
|
|
|
|
x |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
ε + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
D |
|
|
|
∂ ln ρ |
|
|
|
|
∂ ρε |
|
|
|
|
|
7 |
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
D |
|
∂ |
|
lnρ |
|
|
|
|
|
|
||||||||||||||||||||||||
+ |
|
|
|
|
|
|
|
|
|
|
t + |
|
ε t |
∂ |
− |
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||||||||||||
|
Dε + |
|
|
|
|
|
|
∂ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dε + |
|
∂ |
x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ x 3 |
|
|
|
∂ |
|
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь, согласно (8.5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ τ= |
|
|
Dε + dt= |
cµ |
ε∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
Dε + |
|
|
|||||||||||||||||||||||||||||||||||
Как уже отмечалось, значок «+» в коэффициенте диффузии |
|
|
означает, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
что из формулы (8.4) берется только верхнее значение при x > 0 . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
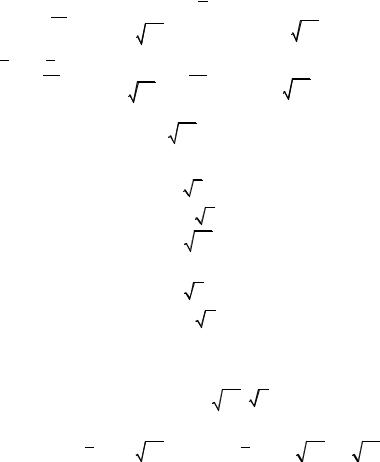
Проведем осреднение по области [ − L2 , |
L1 ] . Значения L1 |
и L2 связаны с |
||||
переменной τ соотношениями |
(8.6). |
Здесь следует |
заметить, |
что |
||
отношение коэффициентов |
Dε |
, |
входящее в (8.7), будет в точке x = |
0 |
||
|
||||||
|
Dε + |
|
|
|
|
|
иметь разрыв, а это нужно учитывать при получении осредненных формул. Окончательный результат после осреднения получим в виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
ε |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|||||
|
|
dk |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
− |
P0 |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
2= |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
; |
|
||||||
|
|
|
2 |
|
|
2 |
4η 12 (1 + β 2 ) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2η 1L (1 + |
β |
2 ) |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
dL |
|
|
|
|
|
L |
|
|
|
cµ k |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
dε |
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
P |
|
|
|
|
|
|
|
|||||||||||||
|
t |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
||||||||||||||||||||
|
|
|
|
− |
|
P |
|
+ |
|
|
|
|
|
ε 2 |
|
|
|
|
|
|
|
t |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
ε 1 1 |
|
|
|
|
|
|
; (8.8) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4η 12 (1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2η 1L (1 + |
β 2 ) |
|
|
|
|
|
|
|||||||||||||||||||||
|
dL2 |
|
|
|
2 L2 |
|
|
β 2 ) 2 cµ k 3 |
|
|
|
|
|
|
|
k |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dL2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 4η 12 (1+ |
|
β |
2 ) |
|
|
|
cµ |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε t |
|
|
|
|
|
|
|
|
|
|
|
||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Φ( |
|
|
|
|
2η 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = − |
0.5− |
|
|
|
|
A02 |
|
|
X |
|
; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
6 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Φ(η |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = |
|
|
|
|
|
|
2 |
gA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2η 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = − |
0.5− |
Φ( |
|
|
|
|
2 η 1) |
A02 |
|
|
X |
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Теперь поясним алгоритм получения выше приведенных формул. Он во многом напоминает процедуру осреднения для k–модели. А именно, использованы следующие формулы:
|
L1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
2 ) |
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
||||
а) |
|
ρ kdx = kM ; |
где M = |
2η |
|
τ ; |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
ρ |
+ ρ |
β |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
− L2 |
|
|
Dε |
|
|
∂ ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
L1 |
|
|
|
|
|
gΦ (η |
|
) β |
|
|
|
ρ( |
|
|
)= |
|
|
|
|
|
2 ) |
|
||||||||||||
б) |
∫ |
g |
|
|
|
|
|
|
|
|
|
dx = |
|
1 |
|
2 |
−ρ |
2 |
gAΦρ |
β |
0 |
+1β |
; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
Dε + |
|
|
|
∂ x |
|
|
|
|
|
|
|
|
|
1 |
|
|
0 1 |
|
2 ( |
|
||||||||||||
|
− L2 |
|
|
|
|
|
|
|
|
∫∂ ρ ∂ ε |
|
|
t |
dx≈ |
0 ; |
|
|
|
|
|
|
|
|||||||||||||
в) ∫ ∂ ρ ∂ k dx ≈ 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
L1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
− L2 |
|
∂ x |
∂ |
x |
|
|
− |
|
|
x∂ |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
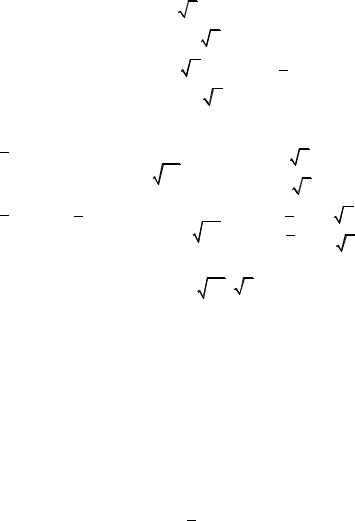
L1 |
|
∂ ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) ∫ |
k |
dx = |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∂ τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
− L2 |
|
|
|
|
|
|
|
|
|
|
|
|
Φ( |
2η 1 ) |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
L1 |
|
|
∂ ln ρ |
2 |
|
D |
|
|
A0 |
X P Mk |
|
|
||||||||||||
д) ∫ |
ρ k |
|
|
|
|
|
|
|
|
ε |
|
dx = |
|
|
|
|
|
|
|
|
|
; |
|
|
|
∂ x |
|
|
|
|
|
|
|
|
|
|
|
|
τ |
||||||||||
− L2 |
|
|
|
|
|
Dε + |
|
|
|
|
4 2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Φ( |
2η 1 ) |
2 |
|
|
|
|
|
|
|
L1 |
|
|
|
∂ ln ρ |
2 |
|
D |
|
|
|
A0 |
X P M ε |
|
|
||||||||||
е) ∫ |
ρε t |
|
|
|
|
|
|
|
ε |
|
dx = |
|
|
|
|
|
|
|
|
t |
. |
|||
|
∂ x |
|
|
|
|
|
|
|
|
|
|
|
τ |
|
||||||||||
− L2 |
|
|
|
|
|
Dε + |
|
|
|
|
4 2 |
|
|
|
|
|
||||||||
Возвращаясь к системе уравнений (8.7) с учетом соотношений а) – е) |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Φ( |
2η 1 ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
d ( |
kM ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
+ |
|
|
ε t |
|
|
|
M = Φ |
(η |
|
) β ρ( −ρ |
|
|
) −g |
|
|
k ; |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 MX |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
0 |
P |
|
|
|
|
|
|
|
|
|
|
|
dτ |
|
|
|
|
c |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 2 |
|
|
τ |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Φ( |
2η 1 ) |
|
|
|
|
|
|
|
|
|
|
||
|
d ( ε t M ) |
|
|
|
|
c |
|
ε |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
2 |
|
|
ε |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(η |
|
) g β |
|
ρ( |
|
|
|
|
) |
|
|
t |
||||||||||||||||||||||||||
|
|
|
|
|
|
+ |
|
|
ε 2 |
|
|
|
t |
|
M = |
cΦ |
|
|
−ρ |
|
|
−t |
|
|
|
|
A |
MX |
|
|
|
|||||||||||||||||
|
dτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P τ |
||||||||||||||||||||||||||||
|
|
|
|
|
c k 3 |
|
ε |
1 |
|
1 |
|
|
|
|
2 |
|
1 |
|
2 |
|
k |
3 2 |
0 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2η 1 (1+ |
|
|
|
2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Используя соотношение L = |
|
β |
|
τ , получим (8.8). |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Если положить β 2 |
= 1, |
что справедливо при числах Атвуда близких к |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
нулю, то |
|
|
в |
системе (8.8) |
следует |
положить |
X P = |
1 |
и A0 |
= A . Такой |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
симметричный случай был изучен в работе [ ].
3. Свойства решений системы (8.8). Решение при кусочно–постоянном ускорении
Исследуем свойства решений системы уравнений (8.8). Заметим, что эти уравнения интегрируются в двух случаях: при постоянном ускорении
|
|
= |
const |
( P = const) , а также при отключенном ускорении |
g |
||||
|
|
|
|
1 |
|
|
= |
0 ( P= |
0) . Последний случай отвечает асимптотическому режиму, |
g |
||||
|
|
|
1 |
|
на который выходит решение задачи о перемешивании слоя смеси с начальной кинетической энергией k ( 0) , имеющего в начальный момент
конечную ширину L0 .
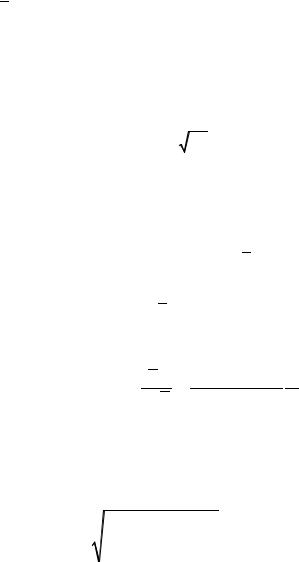
|
Пусть |
|
= const . |
В этом случае, естественно при |
L = 0 принять |
||
|
g |
||||||
ε t |
|
|
|
|
|
|
|
= k = 0 . |
Эта точка |
является особой для системы |
уравнений (8.8). |
||||
Исследование поведения интегральных кривых, проведенное в Приложении 5, показывает, что при нулевых начальных данных решение многозначно: существует однопараметрическое семейство интегральных кривых, удовлетворяющее нулевым начальным данным. Кроме того, помимо этого свойства, есть единственное решение, которое при постоянном ускорении обеспечивает квадратичный закон от времени. Это решение получено в Приложении 5 и имеет вид:
|
|
|
0.5η |
1 |
( |
1+ |
β |
2 ) |
c |
µ |
( c |
− |
c |
1 |
) 2 |
Pt 2 |
|
||
|
|
L = |
|
|
|
|
|
ε 2 |
ε |
|
1 |
. |
(8.9) |
||||||
|
|
2 |
|
|
|
(1− 2P )− |
0.5+ |
|
|
|
|
||||||||
|
|
|
∏ |
|
c |
|
2P |
|
|
||||||||||
|
|
|
|
|
ε i |
|
|
0 |
|
|
|
|
2 |
|
|
||||
|
|
|
i= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
|
= 0 , |
( P = |
0) .Система |
уравнений (8.8) |
значительно |
|||||||||||||
g |
|||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
упрощается
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε t |
|
2 |
|
|
|
|
|
|
|
dk |
= |
|
|
|
k |
P0− |
|
|
|
|
|
; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dτ |
|
|
|
τ |
|
|
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
cµ k |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
dε t |
|
|
ε |
|
|
|
|
|
|
cε 2ε |
|
|
3 |
|
||||||||
|
= |
t |
|
|
P − |
t |
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
dτ |
|
|
|
τ |
2 |
|
cµ |
|
k 3 |
|
||||||||||||
ε |
2 |
|
3P − 1− |
2P |
|
= |
k |
||||
t |
0 |
2 |
|
||
Эта система имеет интеграл |
|
|
|
|
|
cµ k P0 ( 3 − 2cε 2 ) τ
Используя его, получим решения системы уравнений (8.10).
|
|
|
|
|
|
|
|
|
|
τ |
|
Bε |
− 1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Bε |
|
|
|
||||||||
|
|
|
|
|
k = |
|
|
|
|||||||||||||
|
|
|
|
|
k1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
τ1 |
|
|
|
|
|
|
|||||
|
|
|
|
3P − 1− |
2P |
3 |
|
|
|
1 |
|
2 Bε − 3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
2 B |
|
2 B |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
ε t = |
|
k |
τ |
τ |
|||||||||||||||||
cµ P ( 3 |
− 2c ) |
|
1 |
ε |
ε |
||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
2 |
|
|
|
|
||||||
|
|
|
0 |
|
|
|
|
ε 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bε |
= |
|
|
|
1.5 − |
|
cε 2 |
|
|
|
|||||||
|
|
|
|
1 − P2+ |
|
|
cε 2 ( P−0 |
1) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
(8.10)
(8.11)
(8.12)
k1 и τ1 вычисляются согласно формулам |
|
(П.5.3) и (П.5.4) в конце |
||||||||||||||||||||||||||||
интервала t0 , на котором ускорение постоянно: |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
( c |
− |
|
c |
1 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k1 = |
|
|
|
1 |
|
ε 2 |
|
|
ε |
|
|
|
|
|
|
τ1 ; |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
cε 2 |
( 0.5 − |
P0 )− |
|
0.25+ |
P2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c P ( c |
2 |
− |
c |
1 |
) 2 t 2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
τ1 |
= |
|
|
|
µ |
1 |
ε |
|
|
ε |
|
|
0 |
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
P + |
|
|
|
|
( P− |
0.5) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
16 |
0.25 − |
|
c |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∏ |
|
|
|
|
2 |
|
ε i |
|
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Получим формулу для ширины |
L . Решение (8.12) подставим в третье |
|||||||||||||||||||||||||||||
уравнение (8.8), которое может быть представлено в виде: |
|
|
||||||||||||||||||||||||||||
|
dτ |
|
|
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
c |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dt |
|
|
|
ε t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ , а затем для ширины L |
|||||||||
Окончательно получим сперва выражение для |
|
|
||||||||||||||||||||||||||||
при t ≥ |
t0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
cµ k1 |
( 3 |
− 2cε 2 ) |
|
|
Bε |
||||||||||
|
|
|
|
|
τ = |
τ |
1+ |
|
|
(−t t |
|
) ; |
||||||||||||||||||
|
|
|
|
|
|
|
( 3P |
− |
|
1− |
|
2P ) |
τ |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
B |
|
|
|
0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
0 |
|
|
|
|
|
|
|
2 |
1 |
|
|
|
||||
|
|
|
1 |
|
L = L |
1+ |
|||
|
||||
B |
||||
10 |
|
|
||
|
|
|
ε |
|
где L10 = L ( t= |
|
t0 ) . |
||
Обратим внимание,
принимает значение k1 ,
разрывным в силу того,
выражения (П.5.2) при t ≤
ε t2 ( t0 − 0)= ε
cµ k1 ( 3 |
− 2cε 2 ) |
|
|
Bε |
|
|||
(−t |
t |
) |
(8.13) |
|||||
( 3P − |
1− |
2P ) |
τ |
|||||
|
0 |
|
|
|||||
0 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
t = |
t0 |
|
|
|
|
|
|
||||
что |
при |
|
кинетическая |
|
энергия |
k |
|
||||||||
а значение |
фиксированной функции ε t |
будет |
|||||||||||||
что |
при |
ее |
вычислении |
используются |
разные |
||||||||||
t0 и (8.11) при t = |
t0 . Именно: |
|
|
|
|
|
|
|
|||||||
|
0.25 − |
P + |
c |
( P− |
0.5) |
|
|
|
3 |
|
|
|
|
||
|
|
k |
|
|
|
||||||||||
1 |
|
|
2 |
ε 1 |
0 |
|
cµ |
1 |
|
|
|
|
|||
|
|
c |
− c |
|
|
τ |
|
|
|
|
|||||
|
|
|
|
ε 1 |
ε 2 |
|
|
1 |
|
|
|
|
|||
|
|
|
|
P − |
1+ |
2P |
|
|
3 |
|
||
|
|
2 |
( t0 + 0)= |
k |
||||||||
|
||||||||||||
ε t |
P ( 3 |
− |
2c |
) cµ |
τ . |
|||||||
|
|
|
|
0 |
|
2 |
|
1 |
|
|||
|
|
|
|
0 |
|
ε 2 |
|
|
1 |
|
||
Однако, значение ε t |
будет в точке t = |
t0 |
непрерывным в частном случае |
|||||||||
выбора постоянной cε = 1.5.
Таким образом, решение для полной ширины будет определяться формулой (8.9). на интервале [ 0,t0 ] постоянного ускорения и (8.13) при
выключенном ускорении. Формулу (8.10) можно представить в более общем виде, пригодном в и случае медленно изменяющегося ускорения,
если перейти, как и раньше в |
§7 |
для |
lv–модели, от времени |
t к |
|||||||||||||||
перемещению s = |
|
gt 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
) |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
c |
|
Φ A (1 + β |
|
β |
|
( c |
|
− c |
) 2 s |
|
|||||||
L = |
|
|
µ |
|
1 0 |
|
|
2 |
|
|
2 |
ε |
2 |
ε 1 |
|
. |
(8.14) |
||
|
|
|
|
2 |
|
|
|
|
|
|
( 2P− 1) |
|
|||||||
|
|
|
|
|
2 |
|
0.5 − |
2P + |
c |
|
|
|
|||||||
|
|
|
|
|
∏ |
|
|
|
2 |
ε 1 |
|
|
0 |
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Обратим внимание, |
что зависимость от числа Атвуда A проявляется через |
||||||||||||||||||
параметры |
A0 , |
|
|
β 2 , |
P0 , |
|
P2 , |
которые определены выше. |
Позже |
||||||||||
эта зависимость будет исследована более детально.
Из формул (8.13) и (8.14) вытекают важные следствия относительно постоянных ke –модели:
1) степень затухания турбулентного перемешивания при выключенном
ускорении определяется |
только |
постоянной |
cε 2 , 2)интенсивность |
||
турбулентного перемешивания J = |
dL |
зависит линейно от постоянной |
|||
2α s |
|||||
|
|
|
|
||
cµ и разности ( cε 2 − cε 1) , входящей в степени 2. 3) степень затухания |
|||||
турбулентности Bε и интенсивности турбулентного перемешивания J |
|||||
зависят от числа Атвуда |
A через параметры |
A0 , P0 , P2 . Однако, |
|||
чтобы получить окончательные формулы, следует как и в §7 уточнить решение за счет учета дополнительного ускорения.
4. Учет дополнительного ускорения
Прежде чем это сделать, перейдем к частному случаю модели, когда cε 1 = 1.5 . Тогда уравнения (8.8) допускают интеграл, верный как при постоянном ускорении, так и при нулевом. Эта будет формула (8.11). Ее можно переписать, если перейти от τ к L :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 18 − 2Φ |
|
A2 X |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
P |
k |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
ε t = η |
1 cµ (1+ |
β |
|
2 ) |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
(8.15) |
|
||||||||||||||
|
|
|
|
|
3( 2c |
− |
3) |
|
|
|
|
|
L2 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значения |
|
|
A0 и X P |
определены |
в §7 |
(7.39). |
|
Учтем дополнительное |
||||||||||||||||||||||||||||||||||
ускорение, возникающее за счет перемещения u : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
u = − D |
|
∂ |
ln ρ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
ε |
|
|
∂ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ − L2≤ |
x≤ |
L1 ] , |
|||||||||
Усредним |
|
эту скорость |
по |
области перемешивания |
||||||||||||||||||||||||||||||||||||||
предварительно умножив обе части равенства на |
|
ρ . Как и раньше в §7, |
||||||||||||||||||||||||||||||||||||||||
учтем разрывность коэффициента Dε |
. Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
L1 |
|
|
|
|
|
1 |
|
|
|
|
|
A β + (1 |
|
|
) |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|||||||||||||||||||||
|
u |
= − |
|
∫ |
D |
d ρ+ |
∫ |
D |
dρ |
|
= − Φc |
|
|
β |
|
− |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
ε − |
|
|
|
ε + |
|
|
|
|
|
|
µ |
|
|
1 0 |
|
|
2 |
|
2 |
|
|
|
|
|
|
||||||||||||
|
|
|
− |
L2 |
|
|
|
0 |
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε t L |
||||||||||
|
|
|
|
|
|
|
|
− cµ β |
Φ1 A0 |
|
3( 2cε 2 − 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k . |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 η |
1 |
|
18 − 2Φ |
2 |
A2 X |
P |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Здесь использовано соотношение (8.15). Дифференцируя полученную |
|||||||||||||
скорость по времени, получим значение дополнительного ускорения |
|||||||||||||
|
|
|
= − cµ β 2 (1+ |
β 2 ) |
6( 2c |
− 3) AΦ |
|
|
|
|
|
|
|
|
|
|
|
|
|
dk |
|
|
|||||
|
du |
|
1 |
||||||||||
|
|
|
|
ε 2 |
0 |
|
|
|
|
. |
|||
|
dt |
18 − 2Φ 2 A02 X P |
|
dL |
|||||||||
Если его добавить к ускорению g в правые части системы уравнений (8.8),
то окончательно получим:

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Φ1g0 A0 |
|
|
β 2 |
|
|
|
|
|
||||
|
|
|
|
dk |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
||||||||
|
|
Θ |
|
|
|
+ |
|
|
2P |
= |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
(8.16) |
|||
|
|
|
|
|
|
|
|
2η 12 (1 + |
|
|
2 ) |
||||||||||||||||||
|
|
|
0 |
dL |
|
|
3 |
L |
|
|
β |
|
|
|
|
|
|||||||||||||
dL |
= 4η |
|
cµ (1+ |
|
|
β 2 ) |
|
|
3( 2cε 2 |
− |
|
3) |
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
|
|
|
|
k ; |
(8.17) |
||||||||||||||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
18 − 2Φ |
2 A02 X P |
|
||||||||||||||
|
|
P = − |
|
|
P+ |
18 − |
|
2Φ |
A2 X |
P |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
; |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
( 2cε 2 − |
3) |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3 |
|
|
|
|
0 |
|
|
12 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Θ |
0= |
+1 |
|
|
|
|
3( 2cε 2− |
3 ) β 2cµ Φ12 A02 |
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
η 12 (18 − |
|
2Φ 2 A02 X P ) |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Уравнение для интенсивности ε t исключено из рассмотрения с помощью соотношения (8.15). Таким образом, получим систему уравнений (8.16) и (8.17) в переменных k , L, t . Свойства подобных уравнений хорошо
изучены в §7. В том числе и зависимость от ненулевых начальных данных. Вернемся к решению уравнений (8.8) для ускорения, заданного
ступенчатой функцией (7.17), описываемого формулами (8.13) и (8.14). Уточним за счет дополнительного ускорения. Получим, что формула (8.13) и (8.14)перейдут соответственно в следующее:
|
|
|
|
2η 1 (1 + |
|
|
|
2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
β |
|
c |
µ |
k |
( 3 − |
2c |
) |
(−t t |
) |
Bε |
|
|
|
||||||||||
L = |
L |
1+ |
|
|
|
|
|
|
|
|
1 |
|
|
|
ε 2 |
|
|
; |
(8.19) |
|||||||||
|
|
|
|
|
|
|
3P − 1− |
|
|
|
|
|
||||||||||||||||
|
10 |
|
|
L B |
|
|
2P |
|
0 |
|
|
|
|
|
||||||||||||||
|
|
|
|
10 |
|
ε |
|
|
|
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
12c |
µ |
(1 + β |
2 |
) |
β Φ A |
( c |
− c |
1 |
) 2 |
|
|
|
( 2cε 2 |
− 3) |
|
|
|
|||||||||
|
L = |
|
|
|
|
|
2 1 0 |
|
ε 2 |
ε |
|
|
|
|
|
|
. (8.20) |
|||||||||||
|
|
|
|
|
|
Θ + 2P |
|
|
|
|
|
|
18 − 2Φ |
2 |
A2 X |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
3 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||||
Обратим внимание, что вид решения (8.13)сохранился за исключением степени Bε .
|
|
|
|
Θ |
0 |
|
|
Теперь |
Bε = |
|
. |
||||
Θ 0+ |
|
|
|||||
|
|
|
|
|
P3 |
||

Получились довольно громоздкие формулы. Чтобы установить
зависимость |
интенсивности |
турбулентного перемешивания J = |
|
dL |
и |
||||||||||
|
2ds |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
степени затухания турбулентности |
Bε |
как и в §7. Построим графики при |
|||||||||||||
фиксированных |
|
|
эмпирических |
|
постоянных. |
cµ = |
2, |
||||||||
c |
= 1.5, c |
= |
|
15 |
, η = |
2 Φ, |
= |
|
0.89,Φ = |
|
0.97 . |
|
|
|
|
8 |
|
|
|
|
|
||||||||||
ε 1 |
ε 2 |
1 |
π |
|
|
1 |
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
Подчеркнем еще раз, что постоянная cµ |
выбрана так, чтобы интенсивность |
||||||||||||||
перемешивания J для ke и k моделей совпадали при малых числах Атвуда
A . Тогда приходим к следующим простым апроксимационным формулам:
J1 |
= |
dL1 |
= |
0.06(1+ 0.42 A) A ; |
(8.21) |
|||
|
|
|
||||||
|
|
2ds |
|
|
|
|||
|
|
|
|
= |
2+ 0.05A2 L. |
|
||
|
|
|
B |
(8.22) |
||||
|
|
|
ε |
7 |
|
|
||
|
|
|
|
|
|
|
|
|
Сравнение результатов двух моделей показывает, что зависимость интенсивности перемешивания от числа Атвуда получается фактически одной и той же, степень затухания в ke модели – несколько ниже. Эту несущественную разницу трудно заметить экспериментально.
Подчеркнем основной результат, следующий из полученных аналитических формул, как для ke модели – (формулы (8.19), (8.20)), так и для k модели (формулы (7.48) и (7.54)). Интенсивность турбулентного
перемешивания J1 и степень затухания турбулентности Bε довольно заметно зависят от числа Атвуда. Для J1 в литературе принято считать зависимость от числа Атвуда линейной. Здесь установлена нелинейность, из которой следует, что при A = 1, постоянная перемешивания как бы возрастает на 42%. Также степень затухания Bε возрастает на 18%.
5. Влияние начальных возмущений
Ограничимся частным случаем ke уравнений, когда cε 1 = 1.5 , т.е.
будем изучать поведение решения уравнений (8.16), (8.17). Сперва заметим, что подобная система уравнений уже была исследована в §7. (уравнения
(7.12), (7.13), а с учетом несимметрии это система (7.44). Здесь будем исследовать систему уравнений (8.16), (8.17) при ненулевых начальных условиях
t = 0; L= |
|
L0 ; k= |
|
|
|
k0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
При постоянном ускорении из (8.16) имеем решение для |
k |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
2 Φ1 A0 L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
k = |
|
|
|
|
|
|
|
|
4P3 ) + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2(1 + |
|
β 2 )η 12 (Θ +0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β Φ g A L |
|
|
|
|
|
|
|
|
4 P . |
(8.23) |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L Θ 0 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||
|
|
|
+ |
|
|
− |
|
|
|
|
|
|
2 1 0 0 0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
2(1 + |
|
|
|
β 2 )η 1 |
|
(Θ +0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4P3 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что при определенных начальных данных, приводящих к |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
занулению квадратной скобки, получается сразу автомодельное решение. В |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
других случаях будет иметь место выход на автомодельное решение, |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
которое определяется первым слагаемым в выражении (8.23). Второе |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
слагаемое с ростом L стремится к нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
Уравнение для ширины (8.17) после подстановки в него решения (8.23) |
|
|
|
|||||||||||||||||||||||||||||||||||||||
примет вид: |
4(1 + |
|
β 2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
dL |
|
|
|
|
|
|
|
|
|
|
|
3( 2c |
2 |
|
− 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
cµ |
|
|
|
|
|
|
|
ε |
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|||
|
d 2s |
|
|
|
|
|
2 |
|
|
|
|
|
|
18 − 2Φ 2 A0 X P |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
β Φ A L |
|
|
|
|
|
2k |
|
|
|
|
|
|
|
|
|
β Φ A L |
|
L |
Θ 0 |
|||||||||||||||||
× |
|
|
|
|
|
|
|
|
2 1 0 |
|
|
|
|
|
|
+ |
|
|
|
|
η |
12− |
|
|
|
|
|
|
|
|
2 1 0 0 |
|
|
|
|
|
4 P3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||||||||||||||||
(1 + |
|
|
|
β 2 ) (Θ +0 |
4P3) |
g |
|
|
+(1 |
|
β 2Θ) (+ 0 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
4P3) |
|
|
|
|
|||||||||||||||||||||||||||
(8.24) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из полученного уравнения видно, как происходит выход на автомодельное |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
решение. Пусть начальные данные таковы, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
β |
2 Φ1 A0 L0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
k0 |
= |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
g0 |
|
(1 + |
|
|
β 2 )η 12 (Θ +0 |
4P3 ) |
|
|
|
|
|
|
|||||||||||||||||||||
Тогда (8.24) можно проинтегрировать и получить
