Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

Физика

Файл:

Волны / Неуважев В.Е. Математическое моделирование турбулентного перемешивания (2000)

.pdf

Скачиваний:

Добавлен:

15.08.2013

Размер:

1.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 144 5 6 7 8 9 10 11 12 13 14 > Следующая >>>


L =	2α *4		bη		0.9− η	0.1 g4ηb −η1	2 gs ,

		v
L* =		2α *4		bη	0.9− η	0.1 g5 s .

		v

Рис.5.2. Зависимость безразмерной координаты фронтов перемешивания bη 0.1,η 0.01η, 0.η9 , 0.99 g и безразмерной плотности δ b0g от ln n

На рис.5.2 нанесены результаты численного интегрирования уравнения (5.24). Из них следует, что

lim	η		− η	= 0.87+ 0.96= 183. .
n→∞ b		0.9		0.1 g
Поэтому
				lim	L*	=	2α *4	20.5 ,	(5.31)
				lim	s	=	v	20.5 ,	(5.31)
				n→∞	s		v

т.е. предел конечен. Также будет конечно и отношение	L1	при n → ∞	.

	s

Отношение же полной ширины L к s по–прежнему неограниченно растет.

Это следует отнести к недостаткам выбранной модели, с которым можно смириться, так как этот рост происходит за счет «хвоста» малой массы. Между тем в случае, когда в коэффициенте диффузии D использовалась полная ширина, в перемешивание включалась неограниченная масса.

В заключение приведем аналитические формулы приближенного решения, справедливые во всем диапазоне n , если за эффективную

ширину L* принять L* = 2L1 . Для этого воспользуемся результатами численного интегрирования уравнения (5.24), представленными на рис. 5.1

и 5.2. Значение δ b0g с хорошей точностью можно аппроксимировать формулой:

δ	b	g	=	0.5−	0.034 A− 0.006 A3,	=A	n −	1
		0					n +		.	(5.32)
								1
Значения				η 1	и η 2 могут быть	определены,		если		воспользоваться

формулой (5.27), переписанной в виде двух формул:

z0η 1 z2dη

= −

ln ∆ b0g ,

(5.33)

z−0η

z2dη

ln n∆ b0g .

(5.34)

Также будем считать, что

z =

cη 12−

η 2 h,

если

0≤

η ≤

для любых n

(5.35)

z3 = −

2η ,

если −

≤2

η≤

0 для>> n 1 .

(5.36)

Подставим (5.32) в (5.29) и получим

∆ b0g =

1 −

0.068 A2−

0.012 A4

(5.37)

1 +

Из (5.35), (5.37), (5.33) следует

η 15

9 15

для

0≤

A≤

(5.38)

1− 0.068A2−

0.012 A4

Из (5.36), (5.37), (5.34) следует

( − η 2 ) 5=

( ln 2n) 3 ,

для

n>>

1 .

144 18 9

Окончательно получим:

1 +

540

для 0 ≤

A≤ 1

1 −

0.068 A2−

0.012 A4

(5.39)

Здесь использована формула

α *4

b2η 1g5 ,

полученная

из

(5.23) в

предположении,

что

L* =

2L1 .

Безразмерную

плотность ∆

можно получить из уравнения (5.16), которое в переменных

η ,

z имеет вид

∆

′

∆

где значок

означает дифференцирование по

в отличие от (5.16), где

дифференцирование по

. С учетом (5.35), (5.38) получим:

∆ = ∆ ( 0)

x−

1−

для 0 ≤

x≤

L , где ∆ b0g

зависит от

A согласно(5.37).

§ 6. Свойства lv–модели турбулентного перемешивания. Автомодельные решения

вобщем случае

Вэтом параграфе рассмотрены свойства автомодельных решений системы уравнений (5.9) при α 2 = 0 . Роль этого параметра будет отдельно

рассмотрена в § 7. Сперва положим также и β = 0 .

1. Модель перемешивания при α 2 = 0,			β = 0 .
Рассмотрение будем вести в эйлеровых координатах. Исходные
уравнения (5.9) при β = 0	и	α 2 = 0	несколько упростятся.	В
коэффициенты уравнений для ξ	и	∆ войдут постоянные α и v ,		что

неудобно при исследовании общих свойств решения. Оказывается,

существует

преобразование,

приводящее

уравнению,

содержащему в

коэффициентах постоянные α

и v только в комбинации

Это преобразование следующее:

2α 2λ(

−λ

λ) 2

, ξ

λ( −ξ

) ,

=α λ

2 α (λ 1 −λ 2 )

(6.1)

После подстановки (6.1) в (5.9) получим

vξ 2

λ +

ξ ξ

−

2−

−

λ+

0 , (6.2)

′

(λ 1 −λ 2 )

α 2

2 y′

−

ξ ′ =

ξ y

(6.3)

Уравнения

(6.2)

(6.3)

нужно

дополнить

граничными

условиями

(5.11), (5.12) на левой и правой границах перемешивания, которые в новых переменных будут иметь вид

λ = λ 2	: ξ (λ 2 ) = 0, y( λ 2) = −	2	λ	2 ,	(6.4)

	3


λ =	λ 1 : ξ (λ 1) =	0, y( λ 1) =		2	λ	1 .	(6.5)

	y(λ 2 ) и	y(λ 1)	3
Значения функций			устанавливаются				путем

дополнительного исследования поведения решения в окрестности граничных точек, которые для системы уравнений (6.2) и (6.3) являются особыми.

Покажем, что искомое решение должно выходить из точки (6.4) и входить в точку (6.5). Для этого нужно установить, что

2λ

1 g

y1 =

0; y1= ∞ ; >y1

Рассмотрим все допустимые

значения

y1:

0 и

конечно.

y1 = 0 . Система уравнений (6.2)–(6.3) в окрестности точки bλ

1, 0, 0g

примет вид

2 I

1 y

ξ ′ =

−

J ,

y′ = −

3 ξ

Можно показать, что среди решений, выходящих из точки							bλ	1, 0, 0g		нет
искомого, удовлетворяющего			очевидным условиям			ξ	>	0,	y>	0 .
Действительно, разделив одно уравнение на другое, получим
	dξ	=		3y2 − ξ	ξ .
	dy	=		y	ξ .
	dy			y
Видно, что среди кривых, лежащих в					квадранте ξ >	0,		y>	0 ,	нет
решения, проходящего через начало координат.

2)y1 = ∞ . В этом случае уравнения (6.2)–(6.3) эквивалентны урезанной

системе

′+

yξ ξ

−1

ξy

2 y′

′

−

+ ξ

y+2

Безразмерная

комбинация

y2ξ

точке

λ = λ 1 равна нулю.

Действительно, если вернуться к исходным величинам, то

2ξ

≈

∂ ρ

ρ∂ x

т.е. выражение y2ξ есть поток смеси и поэтому на фронте перемешивания

равно нулю.

Последняя система уравнений после сделанного замечания заметно упрощается:

2	λ ξ1 ′ = − y2 ,	y′ =	3	y3	.
3
			4λ 1 ξ

Поделив одно уравнение на другое и проинтегрировав, получим:

dy	= −	y	,	y=	cξ	− 1
						2 .
dξ		2ξ

3)y1 > 0 . y1 – постоянная. Урезанная система примет вид

2			2			F
	λ ξ1	′ = −	y1	,	−	G
3	λ ξ1	′ = −	y1	,	−	G
3						H

2				I		F	2	2 y′I
λ	+	1	ξ	′J	ξ=	G y1 +			J ,

3				K		H		y1 K

откуда неминуемо следует, что

y1	=	2	λ	1,	ξ ′λb 1 g = − λ2	1 .

	3				3

Аналогично исследуется другая точка и показывается, что

y2	=	2	λ	2 ,	ξ ′λb 2 g = − λ2	2 .

	3				3

Разложение решения в окрестности фронтов перемешивания может быть получено в виде рядов соответственно в точках λ 1 и λ 2 :

y =

λ i +

−

λ i3

(λ i

−

λ ) +

L ,

(6.6)

ξ = −

λ i (λ

− λ i ) −

λ i3

(λ i

−

λ ) 2

+ L;

i = 1,2 .

(6.7)

Значения λ 1 и λ 2 неизвестны. Искомое решение должно проходить

еще через одну особую точку,

лежащую

интервале

(λ 2 ,λ 1) .

Действительно,

коэффициент

при

ξ ′ в уравнении

(6.2)

на концах

интервала (λ 2 ,λ 1) принимает разные знаки,

поэтому в некоторой точке

λ 3 обратится в нуль. Эта точка имеет седлообразный характер, поэтому при численном интегрировании преодолевается без особых затруднений.

Заметим, что особая точка λ 3 отвечает лагранжевой координате,

которая в начальный момент совпадала с границей раздела. В этой точке

выполнено условие (5.2), имеющее в безразмерных координатах вид равенства.

	2	λ	3 +		y32ξ 3 =		0 ,		(6.8)
3

что в свою очередь приводит к связи
2			1				vξ 32
		y3	=		ξ 3 +			,
				3		α 2 (λ 1 − λ 2 ) 2
которая является следствием (6.2) и 6.8).
Дополнительное соотношение
			∫λ 1 y 2 dλ =				ln n		(6.9)
			λ 2

замыкает краевую задачу и позволяет найти единственное решение.

Формально задача переопределена: для системы из двух обыкновенных дифференциальных уравнений известны значения искомых функций y и

ξ как при λ = λ 1 , так и при λ = λ 2 (на основании разложений (6.6) и (6.7). Поэтому начиная численное интегрирование из точки λ = λ 1 и

доводя его до точки λ = λ 2 , в которой одна из функций, например, ξ ,

принимает заданное значение, можно получить результаты, когда функция

y будет отлична от значения y = −	2	λ	2 . Однако в действительности

3

этого не происходит в силу особого характера точки. Достаточно

интегрирование довести до точки λ 2 , в которой ξ				=	0 , как условие
y =	−	2	λ 2 выполнится автоматически. В этом убеждают нас результаты

	3
численного интегрирования.				=
	Таким образом, каждой фиксированной точке λ				λ 1 ставится в
соответствие решение, определяемое вплоть до точки				λ	= λ 2 . Интеграл
(6.9)	укажет, какому конкретному значению n отвечает построенное
решение.
	Если требуется найти решение для заданного n ,			то оно вычисляется

итерациями. Следует заметить, что в коэффициент уравнения (6.2) вошло

		v		λ 2 ,λ 1
выражение			, зависящее от интервала интегрирования		и
	α 2 (λ 1 − λ 2 ) 2
	α 2			α	2
комбинации		. Для определения решения с заданной комбинацией
	v			v

применяется метод, в котором неизвестный коэффициент находится вместе с решением путем итераций.

Как уже отмечалось, в принятой модели решение будет определяться

			плотностей n					α	2
начальным	перепадом		плотностей n			и параметром			. Проведем
исследование зависимости решения от этих величин.									v
исследование зависимости решения от этих величин.
Вначале фиксируем n				(n =	10)	и рассмотрим следующие значения
параметра	α 2	: 0.0018;	0.061; ∞		. Параметр		α 2	, как будет показано в §
	v						v

7, определяет степень затухания турбулентного перемешивания при выключенном ускорении, поэтому область его изменения фактически определена. Однако представляет интерес рассмотреть его влияние на профиль решения.

Результаты сравнения представлены на рис. 6.1. По пространству

выбрана переменная λ 1 , так что правые концы профилей совмещены.

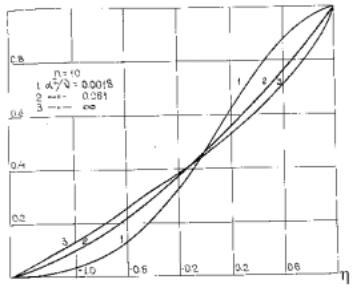
Рис. 6.1. Профиль безразмерной плотности δ				в зависимости от параметра
α 2	при n = 10,		β = 0 , здесь переменная η	=	λ	.
	при n = 10,		β = 0 , здесь переменная η	=		.
v					λ 1
						α	2
	Из сравнения следует, что при изменении параметра						в довольно
широком диапазоне значений от 0.061 до ∞							v
широком диапазоне значений от 0.061 до ∞				различия между профилями
(кривые 2 и 3)							α	2
(кривые 2 и 3)		несущественны. С другой стороны, для значений						в
								v
интервале 0 < α		2	< 0.0018 профиль безразмерной плотности (кривая 1)
		v

мало отличается от профиля в приближении Беленького–Фрадкина на интервале от λ 0.1 до λ 0.9 . На фронтах перемешивания различия будут существенными из–за негладкого примыкания профиля в рассматриваемом

случае (см. разложение (6.6):	∆ ′	(λ = λ i ) =	2	λ i (− 1) i − 1 ,	i = 1,2 ). Из
			3
	∆

<<< < Предыдущая 1 2 34 / 144 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в папке Волны

#
15.08.201330.89 Mб136Крауфорд Ф. Волны.pdf
#
15.08.201330.99 Mб93Лайтхилл Дж. Волны в жидкостях.pdf
#
15.08.20131.54 Mб45Неуважев В.Е. Математическое моделирование турбулентного перемешивания (2000).pdf
#
15.08.201323.96 Mб576Рабинович М.И. Трубецков Д.И. Введение в теорию колебаний и волн.pdf