Ledeneva_T_M_Algoritmy_teorii_grafov_Kodovye

31

Связь между наиб ольш ими независимыми множествами и наиб оль- ш имипаросочетаниямиустанавливаетсяспомощ ью реб ерныхграфов.

ПРИ М ЕРЫ

1.И сточник информации посылаетсооб щ ения, являю щ иесяпоследо-

вательностями сигналов из множестваX = {x1, ..., xm}. П рипередачевследствие помех возникаю т искажения сигналов, поэтому напринимаю щ ей станциинекоторыесигналы могутб ыть приняты задругие, т.е. перепутаны. Рассмотрим граф G, в котором каждому сигналу соответствуетверш ина, а реб ро (xi, xk) присутствуеттогдаитолько тогда, когдасигналы xi иxk могут б ыть перепутаны. Т огда, чтоб ы получить б езош иб очный код следуетпользоватьсясигналами из независимого множестваверш инграфаG. Стремлениеполучить максимальноеколичество таких сигналов приводитк задаче отысканиянаиб ольш его независимого множестваверш инв графеG.

2. И меетсяn проектов, которыедолжны б ыть выполнены, причем для реализациинекоторого проектаxi треб уетсянекотороеподмножество Ri наличныхресурсов из множества{1, ..., r}. П редположим, что каждыйпроект, задаваемый совокупностью ресурсов, можетб ыть выполнензаодини тот жепромежуток времени. П остроим граф G, каждаяверш инакоторого соответствуетпроекту, ареб ро (xi, xk) - наличию об щ ихсредств об еспеченияу проектов xi и xk, то есть условию Ri Ç Ri = Æ. М аксимальноенезависимое множество графаG представляетсоб оймаксимальноемножество проектов, которыеможно выполнить одновременно заодинитотжепромежуток времени. В практическихситуацияхб ываетвесьманепросто выполнить множество проектов, соответствую щ их максимальному независимому множеству наданном отрезкевремени, поскольку исполнениенекоторыхпроектов можетб ыть по каким-то причинам отложено. Т огдакаждому проекту ставитсяв соответствии ш траф, который увеличиваетсясростом времени отсрочкив исполнениипроекта, ив каждыйрасчетныймоментвремени надо выб ирать из семействамаксимальныхнезависимыхмножеств такоемножество, которое максимизирует некоторую функцию ш трафов наверш инах, содержащ ихсяв выб ранном множестве.

3. З адача он аим ен ьш ем покр ы т ии (З НП): пусть At - транспонирован-

ная матрицасмежности графас единичными диагональными элементами. Задачаопределениянаименьш его доминирую щ его множестваграфаG эквивалентназадаченахождениятакого наименьш его множествастолб цов в матрицеAt , что каждаястрокаматрицы содержитединицу хотяб ы в одном из выб ранныхстолб цов. Задачао поискенаименьш его множествастолб цов, “покрываю щ их” всестроки, известнакак задачао наименьш ем покрытии. В об щ ей ЗН П матрица, состоящ аяиз 0 и 1, необ язательно являетсяквадратной. К рометого, каждому столб цу j сопоставляетсянекотораястоимость cj и треб уетсявыб рать покрытие(или, в другой терминологии - доминирую - щ еемножество верш ин) снаименьш ейоб щ ейстоимостью . Заметим, что задачаопределениянаименьш его доминирую щ его множестваесть ЗН П сcj = 1 длявсехj.

32

4. П редположим, что верш ины неорграфаG представляю таэропорты, ареб раэтапы полетов (б еспосадочныеперелеты), которыеосущ ествляю т- сяв заданноевремя. Л ю б ой марш рутв этом графе(удовлетворяю щ ийряду условий, которыемогутвстретитьсянапрактике) соответствуетнекоторому реально выполнимому марш руту полета. П усть имеетсяN такихвозможных марш рутов и длякаждого из нихопределенаего стоимость. Задачанахождения множества марш рутов, имею щ его наименьш ую суммарную стоимость и такого, что каждый этап полетасодержитсяхотяб ы в одном вы- б ранном марш руте, являетсязадачейо наименьш ем покрытиисматрицейT, в которой элементtij равен1, если i-й этап содержитсяв j-ом марш руте, и равен0 в противном случае.

4. С помощ ью понятия доминирую щ его множествареш ается задача размещ ения“центров”, покрываю щ ихзаданную об ласть:

∙размещ ениетелевизионной или радиопередаю щ ейстанциинанекоторой территории;

∙ размещ ениевоенныхб аз, контролирую щ ихданную территорию ;

∙размещ ениецентров торговли, об служиваю щ ихнекоторыйрайон.

5.И меетсямножество населенных пунктов, связанных дорожной сетью . В некоторых из них надо разместить предприятияоб служиваниятак, чтоб ы расстояние от каждого из населенных пунктов до какого-либ о из предприятийнепревосходило заданнойвеличины. Размещ ениеследуетвыполнить так, чтоб ы об ойтись минимальным числом предприятий. Е сли поставить в соответствиенаселенным пунктам верш ины графа, в котором две верш ины смежны тогдаи только тогда, когдарасстояниемежду соответствую щ имипунктаминепревыш аетзаданнойвеличины, то задачасводитсяк

построению в графенаименьш его доминирую щ его множества.

6. З адача он азн ачен иях. И меетсяконечноемножество исполнителей {x1, ..., xn}, каждыйиз которыхможетвыполнять некоторыеиз раб от{y1, ...,

первых, выполнить всераб оты, аво-вторых, минимизировать об щ иезатраты. Строитсядвудольный взвеш енный граф, в котором дведоли X и Y, каждоереб ро означает, что соответствую щ ий исполнитель можетвыполнить раб оту, авесреб ра- wij. В озможность выполнениявсехраб отравносильна сущ ествованию в графесоверш енного паросочетания, аназначение, минимизирую щ еевсезатраты, соответствуетнаиб ольш ему паросочетанию сминимальным суммарным весом.

З АД АЧ И И У П РАЖ НЕНИ Я

1. П ривестипример, показываю щ ий, что каждоереб ро в неорграфеG содержитсяровно в (n-2) треугольниках, но граф необ язательно совпадаетс

независимого множестваВ Х \ А справедливо неравенство |B| ≤ |Г (В ) А |.

33

3. П оказать, что для лю б ых двух графов G¢ и G¢¢ справедливо неравенство a(G¢´ G¢¢) ³ a(G¢) × a(G¢¢), гдепроизведениеG¢´G¢¢ двух гра-

фов G¢=(X¢,U¢) иG¢¢=(X¢¢,U¢¢) есть граф Н =(Y,B), у которого Y = { xi,xj |

xiÎX¢, xjÎX¢¢}, B={ ( xixj, xkxl ) | xi=xk и(xj,xl) Î A¢¢ или xj = xl и( xi, xk ) Î A¢¢ или( xi, xk ) Î A и(xj,xl)ÎA¢¢ }.

4. Д ляпередачи информациииспользуетсяn символов (б укв) из множестваX = {x1, x2, … , xn}. Рассмотрим граф G = (X, A), в котором (xi, xj) ÎА тогдаи только тогда, когдасимволxi можетб ыть спутанссимволом xj на приемном конце канала связи. Символы использую тся в б локах – k- б уквенных“словах”. П оказать, что число, равноенаиб ольш ему числу слов, которыеможно использовать дляб езош иб очнойпередачиинформации, совпадаетсчислом независимостиa[Gk] графаGk = G´G´… ´G (k раз).

5.П усть G - неорграф. О б основать неравенство a(G) ³ b(G), показав, что каждое максимальное независимое множество есть доминирую щ ее множество.

6.Д ляграфов, изоб раженныхнарис.6, перечислить всемаксимальные независимые, найтинаиб ольш еенезависимоемножество, найтичисло независимости.

Рис.6 7. Д ляграфов, изоб раженных нарис.7, определить наиб ольш ую кли-

ку, построить граф клик.

Рис.7

34

8.П усть орграф допускаетфункцию . П оказать, что лю б оемножество верш ин, накотором функцияГ рандипостоянна, являетсянезависимым.

9.П ривести пример, показываю щ ий, что наименьш еедоминирую щ ее множество можетнеб ыть независимым.

10.П усть G - неорграф б ез изолированныхверш ин. Д оказать, что до-

полнение `D минимального доминирую щ его множестваявляетсядоминирую щ им множеством.

11.П ривестипример орграфасчетырьмяверш инами, имею щ его лиш ь одно минимальноедоминирую щ еемножество, состоящ ееприэтом из единственнойверш ины.

12.О пределить минимальныедоминирую щ иемножестваграфов, изо-

браженныхнарис.8.

13.Д оказать, что конечныйграф б ез петель, несодержащ ийконтуров нечетнойдлины, об ладаетядром.

14.Д оказать, что в неорграфекаждоемаксимальноенезависимоемножество являетсяядром.

15.Д ляграфов, изоб раженныхнарис. 9, перечислить всеядра.

Рис.9 16. П редположим, что некоторая фирмананимает переводчиков с

французского, немецкого, греческого, итальянского, испанского, русского и китайского языков наанглийский, приэтом имеетсяпять кандидатур – А , B, C, D, E. К аждаякандидатуравладееттолько некоторым соб ственным подмножеством из указанного выш емножестваязыков.

35

Т реб ованиянаоплату трудау всеходинаковые. Н еоб ходимо реш ить, какихпереводчиков (суказанныхвыш еязыков наанглийский) надо нанять, чтоб ы затраты назарплату б ылинаименьш ими.

4.З АД АЧ А РАС К РАС К И

Некоторыезадачи, возникаю щ иеприпланированиипроизводства, со-

ставлении графиков осмотраи транспортировки товаров, могутб ыть представлены как задачи теории графов, тесно связанныестак называемой “задачейраскраски”, котораяформулируетсяследую щ им об разом: дляданного графаопределить минимальноеколичество цветов, необ ходимых дляраскраски верш инграфатак, чтоб ы никакиедве смежные верш ины не б ыли окраш ены в одинцвет.

Реберной раскраской неорграфа G=(X,U) k цветами называется функция j: U ® {1,2, ..., k}, такая, что длялю б ыхдвухреб ер u1 и u2 вы-

циклов нечетнойдлины. Д оказать, что G имеетреб ерную 2-раскраску, в которойоб ацветапредставлены в каждойверш инестепенинеменее2.

В ерши нной раскраской графаG = (X, U) r цветаминазываетсяфункцияf: X ® {1, 2, ..., r}, такая, что длялю б ыхдвухсмежныхверш инх1 их2 выполняется f(х1) ¹ f(х2), f(х) называется ф ункци ей раскраски . Хром ати чески м чи слом графаG g(G) называетсянаименьш еетакоеr, что

од ноцветным классом .

Д ляхроматического числасущ ествую тследую щ иеоценки: а) нижниеоценкидляg(G):

1.g(G) ³ r(G), ( Зыков )

2.g(G) ³ [ n / a(G) ],

3.g(G) ³ n / g(`G), ( Н ордхауз, Г аддум )

4.g(G) ³ n2 /( n2-2m); ( Г еллер )

5.еслиграф содержитполныйподраф наm верш инах, то g(G) ³ m; б ) верхниеоценкидляg(G):

6.g(G) £ 1+ max[ d(xi) + 1 ], ( Брукс)

36

xiX

7. g(G) £ n+1- g(`G ). ( Н ордхауз, Г аддум )

Замечание. Д ляхроматических чиселграфаG и его дополнения`G имею тместо неравенства

2 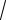n £ g( G ) + g(`G ) £ n+1; n £ g( G ) × g(`G ) £ ((n+1)/2)2.

Г раф называетсякри ти чески м , если удалениелю б ой из его верш ин вместесинцидентнымиейреб рамиприводитк графу сменьш им хроматическим числом.

¨Упраж нение[1, стр. 168] . Д оказать, что всякий критический граф, являю щ ийсяr-хроматическим, об ладаетследую щ имисвойствами:

а) онсвязен;

б ) степень каждойверш ины неменьш е(r-1);

в) несущ ествуетверш ины, удалениекоторой приводитк несвязному графу.

Пусть G - помеченный граф. К аждаяего g-раскраскапорождаетраз-

биениемножестваверш инна g одноцветныхклассов. Е сли g = n икаждая n-раскраскаграфапорождаетодно ито жеразб иениемножестваХ , то граф

G называетсяод нозначно раскраши ваем ым .

♦Упраж нение [1, стр. 165]. Д оказать, что каждый однозначно n- раскраш иваемыйграф связен.

Рассмотрим некоторыепроцедуры раскраш иванияграфа.

Эвр ист ическая пр оцедур а р аск р аш иван ия гр афа

Ш аг 1. G - данный граф. Д лякаждой верш ины графаопределить ее степень. Расположить верш ины в порядкеневозрастанияихстепеней.

Ш аг 2. П ерваяверш инаокраш иваетсяв цвет№ 1; затем список вер- ш инпросматриваетсясверху вниз и в цвет№ 1 окраш иваетсявсякаявер- ш ина, котораянесмежнасдругой, ужеокраш еннойв этотцвет.

Ш аг3. В озвращ аемся к первой в спискенеокраш енной верш ине, окраш иваем еев цвет№ 2 и, двигаясь по списку, окраш иваем верш ины в цвет № 2 так же, как окраш ивалив цвет№ 1.

Ш аг 4. П роцедурапродолжаетсядо техпор, покавсеверш ины неб у- дут окраш ены. К оличество использованных цветов б удет приб лиженным значением хроматического числа.

Замечание: П роцедура позволяет определить лиш ь приб лиженное значение y¢(G) хроматического числаi g(G), которое удовлетворяетсоотно-

ш ению g(G) £ y¢(G) £ max min { d(i)+1, i }, гдеd(i) - степень i-ой верш ины

(индексацияверш инхi осущ ествляетсяв соответствии суб ыванием ихстепеней), причем примененнаяк одному итому жеграфу онаможетдать различные варианты раскраски. Н арис.1 представлены различные раскраски графа, в первом случаехроматическоечисло равно 4, аво втором – 2.

37

Рис. 1

М одифик ация пр оцедур ы р аск р аш иван ия гр афа

Ш аг 1. П оложить r=1 (r - приб лиженноезначениехроматического чис-

ла).

Шаг 2. G(X) - рассматриваемый граф намножестве верш инХ . Д ля каждойверш ины определить степень ирасположить верш ины в порядкеневозрастанияихстепеней.

Шаг 3. П ерваяверш инаокраш иваетсяв цветr ; затем список верш ин просматриваетсясверху вниз ив цветr окраш иваетсявсякаяверш ина, котораянесмежнасдругой, ужеокраш енной в этотцвет. Sr - множество вер-

шин, окраш енныхв цветr.

Ш аг 4. П оложить Х = Х \ Sr . Е слиХ ¹ Æ, то намножестве верш ин Х получить порожденныйподграф G(X) ; положить r = r + 1 иперейтик ш агу 2. И начеостанов - всеверш ины графаокраш ены, r - приб лиженное значение хроматического числа.

Е сли известно, что граф G r-хроматический, то онможетб ыть раскраш енсиспользованием r красок спомощ ью следую щ ейпр оцедур ы , осн о-

ван н ой н а опр еделен ии м аксим альн ы х н езависим ы х м н ож ест в: сначалав одинцветокраш ивается некоторое максимальное независимое множество S[G], затем окраш иваетсяв следую щ ий цветмножество S[ X \ S[G] ] и т.д. до техпор поканеб удутраскраш ены всеверш ины.

Замечание. П оскольку при лю б ой допустимой раскраске графа G множество верш ин, окраш иваемыхв одинитотжецвет, должно б ыть независимым множеством, то всякую допустимую раскраску можно интерпретировать как разб иениевсехверш иннатакиенезависимыемножества. Е с- ли, при этом, каждоенезависимоемножество расш ирить до максимального (путем доб авления к нему других верш ин), то раскраскаграфаG может б ыть истолкованакак покрытиеверш инграфаG максимальныминезависимымимножествами. О чевидно, что в последнем случаенекоторыеверш ины графаG могут принадлежать б олеечем одному максимальному независимому множеству. Э то говорито возможностисущ ествованияразличныхдопустимых раскрасок (использую щ их одно и то же число цветов), так как верш ину, принадлежащ ую разным максимальным множествам, можно ок-

38

расить в лю б ой из цветов, соответствую щ их тем максимальным независимым множествам, которым онапринадлежит.

ПРИ М ЕРЫ

1.З адача ор аск р аск е как задачао наименьш ем покрытии (ЗН П ): За-

метим, что при лю б ой допустимой раскраскеграфаG множество верш ин, окраш иваемых в одини тотжецвет, должно б ыть независимым множеством. П усть построены всемаксимальныенезависимыемножества. Рассмотрим матрицу M = {mik}, у которойmik = 1, есливерш инаi принадлежитk-му максимальному независимому множеству и 0 - иначе. Е слитеперь каждому максимальному независимому множеству сопоставить единичную стоимость, то задачараскраскисведетсяк задаченахождениянаименьш его числастолб цов в матрицеМ , покрываю щ их всееестроки. (i -й столб ец в 0-1 матрицепокрываеттеи только тестроки, в которых напересечении сi-м столб цом стоят1). К аждыйстолб ец из реш енияэтойЗН П соответствуетопределенному цвету, который может б ыть использован для окраски всех верш ин максимального независимого множества, представленного этим столб цом.

2.З адача сост авлен ия р асписан ий. П редположим, что необ ходимо прочитать несколько лекций закратчайш еевремя, причем некоторыелекции немогутчитатьсяодновременно (например, их читаетодини тотже лектор). П остроим граф G, верш ины которого соответствую тлекциям, адве верш ины смежны тогдаи только тогда, когдасоответствую щ ие лекции нельзя читать одновременно. О чевидно, что лю б ая правильная раскраска этого графаопределяетдопустимоерасписание: лекции, соответствую щ ие верш инам графа, составляю щ иеодноцветный класс, читаю тсяодновременно. И , об ратно, лю б оедопустимоерасписаниеопределяетправильную раскраску графа G. О птимальные расписания соответствую т минимальным раскраскам, ачисло часов, необ ходимоедляпрочтениявсехлекций, равно хроматическому числу.

3.Рассмотрим задачур азм ещ ен ия n предметов по ящ икам. П усть каждыйпредметсоответствуетопределеннойверш инеграфа. В сякийраз, когда двапредметаxi и xk немогутб ыть помещ ены в одинящ ик, в графеG вво-

дитсяреб ро (xi, xk). Е сли ящ ики имею тнеограниченную вместимость, так что в каждыйиз нихможно поместить сколько угодно предметов, то задача определениянаименьш его числаящ иков дляразмещ енияпредметов эквивалентназадаченахожденияхроматического числаграфаG, причем каждому ящ ику соответствует определенный цвет, апредметы, окраш енные в одинцвет, укладываю тсяв одинитотжеящ ик.

4. П усть для выполнения каких-либ о n раб от надо распределить m имею щ ихсяв наличииресурсов. Считаем, что каждаяиз раб отвыполняется занекоторыйпромежуток времени, одинаковыйдлявсераб отичто длявыполнения i-й раб оты треб уетсяподмножество ресурсов Si. П остроим граф G: каждой раб отесоответствуетверш ина, реб ро (xi, xk) сущ ествуеттогдаи только тогда, когдадлявыполненияi-йиk-йраб оттреб уетсяхотяб ы один

40

8.В плоскости проведено конечное число об ластей. П оказать, что достаточно двацветадлятакой раскраски графавсехэтихоб ластей, когда лю б ыедвесмежныеоб ластиокраш иваю тсяв разныецвета.

9.О пределить раскраску графов, изоб раженныхнарис.3.

Рис.3

Рис.3 (продолжение)

9. Г раф нарис.4 представляетсхему электрическихсоединений: вер- ш ины соответствую т клеммам, реб рапрямым металлическим полоскам проводников. Д ля физически осущ ествимых соединений проводники не должны пересекать друг друга, поэтому необ ходимо распределить реб рапо нескольким параллельным платам, в каждой из которыхпроводники непересекались б ы. (К леммы доступны навсехплатах). О пределить наименьш ее число плат, необ ходимыхдляреализацииэтихсоединений.