
Ledeneva_T_M_Algoritmy_teorii_grafov_Kodovye
.pdfМ И Н И СТ Е РСТ В О О БРА ЗО В А Н И Я РО СИ Й СК О Й Ф Е Д Е РА Ц И И
Воронежскийгосударственныйуниверситет
Кафедраматематическихметодов исследованияопераций
ЛеденеваТ .М ., РуссманИ .Б.
А ЛГОР И ТМ Ы ТЕ ОР И И ГР А Ф ОВ . К ОД ОВ Ы Е ГР А Ф Ы .
У чеб ноепособ иепо курсу “Д искретнаяматематика” длястудентов дневного ивечернего отделенийфакультетаП М М
В оронеж 2002
У Д К 519.15
2
Л еденеваТ .М ., Руссман И .Б. А лгоритмы теории графов. К одовые графы: У чеб . пособ ие. В оронеж: И зд-во В Г У , 2002. 85 с.
В учеб ном пособ ии излагаю тсяосновы теории графов; представлены разнооб разныеалгоритмы, связанныеснахождением структурныхичисловыххарактеристик графов; приводятсяпримеры сведенияприкладныхзадач к задачам теорииграфов ииспользованииаппаратаэтойтеории. О тдельная главапосвящ енаэлементам теориикодированияикодовым графам. К аждая главасопровождаетсязадачамииупражнениями.
У чеб ноепособ иепредназначено длястудентов, об учаю щ ихсяпо специальности “П рикладная математика”, но может оказаться полезным студентам технических факультетов, изучаю щ их курс “Д искретнаяматематика”.
Рецензент: д.ф.-м.н., профессор Берколайко М .З.
П ечатается по реш ению Н аучно-методического совета факультета прикладнойматематики, информатикиимеханикиВ Г У
В В ЕД ЕНИ Е
О снову теории графов составляетсовокупность методов и представлений, сформировавш ихся при реш ении конкретныхприкладныхзадач.
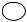
3
Г раф есть совокупность точек илиний, соединяю щ ихэтиточки, причем соединения могут об ладать различными характеристиками. В этой связи граф можно рассматривать как математическую модель длявсякойсистемы, содержащ ей б инарныеотнош ения, поэтому как теоретическаядисциплина теория графов является разделом дискретной математики, исследую щ им отнош ениямежду конечнымимножествамиоб ъектов. М ожно выделить два основных типазадач в рамках теории графов. В первом случаетреб уется ответить на вопрос, сущ ествую т ли графы, об ладаю щ ие определенным свойством, и еслида, то сколько ихиликаково ихмаксимальноеколичество. В другом случае нужно определить, как построить граф или подграф, об ладаю щ ийнекоторым заданным свойством.
К ак прикладная дисциплинатеория графов является замечательным инструментом дляформализации целого рядазадач, связанных сдискретным размещ ением об ъектов. К ним, в частности, относятся: проектирование и исследованиесетей связи, электрических и монтажных схем, программных систем; исследованиеавтоматов, анализ и синтез логических цепей; задачи календарного планирования; поиск информации; разраб откастратегий инвестиций, анализ качества, исследованиедвижениятранспорта, раз-
мещ ение предприятий коммунального об служивания, |
исследованиепове- |
денияиндивидуумов. |
|
1.1. О С НО В НЫ Е П О НЯ Т И Я |
|
П усть задано некоторое конечное множество Х , |
элементы которого |
б удем называть верш инами, и множество U , состоящ ееиз пар элементов (xi,хj) множестваХ . У порядоченнаяпарамножеств G = (X,U) называется граф ом . Е сли в определении графасущ ественно, в каком порядкевыб ира- ю тсяверш ины (т. е. пара(xi ,хj) отличнаотпары (xj ,хi)), то такой граф называю ториентированным или орграф ом , апару (xi, хj) - д угой, при этом считается, что xi - начальная, ахj – конечнаяверш ины дляданнойдуги. Е с- ли начало и конец дуги совпадаю т, то онаназываетсяпетлей. В геометрической интерпретации дуге соответствует направленный отрезок. Е сли в определенииграфанесущ ественпорядок верш инприоб разованиипары (xi ,хj), то граф называю тнеориентированным или неорграф ом , апару (xi ,хj) - ребром . Г раф, полученныйиз орграфазаменойкаждойдугинареб ро, назы-
ваетсяосновани ем орграф а.
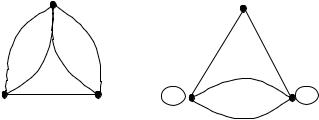
Е сли верш ины графасоединены б олеечем одним реб ром (дугой), то такой граф называетсям ульти граф ом (рис.1, а)), ареб ра(дуги) – кратными. М ультиграф недопускаетпетель. О рграф скратнымидугамиипетлями называетсяпсевд ограф ом (рис.1, б )). Г раф, несодержащ ий петель и кратныхреб ер (дуг), называетсяпростым .
Заметим, что всякийграф G = (X,U) определяетотнош ениенаХ .
4
а) |
б ) |
|
Рис.1. |
Справедливо и об ратноеутверждение: еслиХ – конечноемножество, |
|
то всякоеотнош ениенаХ |
определяетграф, у которого множество верш ин |
совпадаетсХ . И з этого фактаследует, что многиепонятиятеории б инарныхотнош енийраспространяю тсянаграфы. В частности, операции, вводимыедляотнош ений, атакжесвойстваотнош ений порождаю таналогичные определения для графов. Г раф G=(X,U) является си м м етри чески м , если длялю б ойдуги(xi ,хj) U сущ ествуетпротивоположно ориентированнаядуга(xj, хi). П редположив, что реб ро равноценно двум противоположно направленным дугам, можно утверждать, что всякийнеориентированныйграф является симметрическим. Г раф называется анти си м м етри чески м , если каждая парасмежных верш инсоединенатолько в одном направлении и петли отсутствую т. Н арис.2 представлены: а) симметрический орграф, б ) антисимметрический орграф, в) полный антисимметрический орграф. Рефлексивному б инарному отнош ению соответствует граф с петлями. К роме того, для графаможно рассматривать такое свойство как транзитивность. Г раф называется транзи ти вным , если длякаждой пары дуг (x, y) и (y, z) сущ ествуетдуга(x, z), котораяназываетсятранзитивно замыкаю щ ей.
Д веверш ины xi и хj |
называю тся см ежным и , если сущ ествуетсоеди- |
няю щ ее их реб ро (дуга), |
при этом верш ины называю тся и нци д ентным и |
этому реб ру (дуге), ареб ро (дуга) – и нци д ентным (-ой) этим верш инам. |
|
А налогично, дваразличныхреб ра(дуги) называю тсясм ежным и , если они имею т, по крайней мере, одну об щ ую верш ину. В ерш ина, длякоторой не сущ ествуетинцидентных ей реб ер, называется и золи рованной. В ерш ина, длякоторой сущ ествуеттолько одно инцидентноеейреб ро, называетсяви -
сячей.
Д ваграфаG1 и G2 называю тся и зом орф ным и , если сущ ествуетвзаимно однозначноеотоб ражениемежду множествамиихверш ин, сохраняю - щ еесмежность. Э то отоб ражениеназываетсяи зом орф и зм ом . Д ваорграфа изоморфны, если сущ ествует изоморфизм между их основаниями, сохраняю щ ий порядок верш иннакаждойдуге. И нвари антграфаG – это число, связанноесG, котороепринимаетодно и то жезначениеналю б ом графе, изоморфном G. П олныйнаб ор инвариантов определяетграф сточностью до изоморфизма.
П утем в графеG называетсятакаяпоследовательность дуг, в которой конец каждойпредыдущ ейдугисовпадаетсначалом следую щ ей.

|
|
5 |
|
|
x2 |
|
x2 |
x1 |
x3 |
x1 |
x3 |
|
|||
x5 |
x4 |
x5 |
x4 |
|
а) |
x2 |
б ) |
|
x1 |
x3 |
|
|
|
|
x5 
 x4
x4
в)
Рис. 2 Д ля неорграфатакая последовательность реб ер называется цепью. Е сли
путь (цепь) проходитчерез верш ины x1 ,...,хk, то б удем об означать его (ее) символом [ x1 ,...,хk ]. П од д ли ной пути (цепи ) подразумеваетсяколичество дуг (реб ер), которыесоставляю тэтотпуть (цепь). Е сликаждойдуге(реб ру) приписано некоторое число, называемой весом, то граф называется взве- ш енным. Т огдадлинапути(цепи) – это суммавесов дуг (реб ер), входящ ихв этотпуть. П уть (цепь) называется простым (-ой), если в нем никакаядуга (реб ро) не встречается дважды, и составным (-ой) – в противном случае.
Простаяцепь сn верш инамиоб означаетсячерез Pn . П уть (цепь) называется элем ентарным (-ой), если в нем ни однаверш инаневстречаетсядважды.
Путь (цепь), у которого(-ой) начальнаяи конечнаяверш инасовпадаю т, на-
зываетсяконтуром ( ци клом ).
Рассмотрим графы, об ладаю щ иеопределеннымисвойствами.
Г раф, в котором лю б ые две верш ины смежны, называется полным . П олный граф наn верш инах об означаетсяKn . П олный орграф называется турни ром . Э тоттерминполучилсвоеназваниеотсоревнований по круговой системе, графическоепредставлениекоторыхимеетструктуру полного ориентированного графа. В турнирахпо круговой системеиграю тнесколько команд, каждаясо всеми остальными по одному разу. И грапо правилам неможетзакончитьсявничью . В представленииграфом командам соответствую тверш ины, а дуга(x, y) присутствуеттогдаитолько тогда, когдакомандаx поб едилакоманду y. К оличество очков команды соответствуетчислу поб ежденныхею противников.
Г раф G, который можно изоб разить наплоскоститак, чтоб ы никакие двареб ранепересекались в точках, отличных отверш ин, называетсяпланарным графом. Т акойрисунок называю ткарт ой G.
6
♦Упраж нение([5], стр. 231). П оказать, что графы K5 и K3,3 неявля-
ютсяпланарными.
Графы, об разованныеверш инами и реб рами пятиправильныхмногогранников - платоновыхтел: тетраэдра, куб а, октаэдра, додекаэдраиикосаэдра, называю тсяплатоновым и графами. Заметим, что всеплатоновы графы являю тсяполными.
Граф G=(X,U), множество верш инкоторого можно разб ить надванепересекаю щ ихся множестваХ 1 и Х 2 так, что каждоереб ро в G соединяет
какую -ниб удь верш ину из Х 1 с какой-либ о верш иной из Х 2 , называется д вуд ольным . П олныйдвудольныйграф, в котором |X1|=n, |X2|=m об означаетсячерез Kn,m .
♦Упраж нение ([1], стр.32; [2], стр. 21; [6], стр. 36) . Д окажите, что граф G являетсядвудольным тогдаитолько тогда, когдавсепростыециклы в нем имею тчетную длину (теоремаК енига).
Е слизаданграф G, то отнего можно перейтик реб ерному идополнительному графам.
Реберным графом L(G) простого графаG называетсяграф, верш ины которого взаимно однозначно сопоставлены реб рам графаG, причем две верш ины в L(G) смежны тогдаи только тогда, когдасоответствую щ иеим реб расмежны в G.
♦Упраж нение([1], стр. 92). Д оказать, что связныйграф G изоморфен своему реб ерному графу L(G) тогдаитолько тогда, когдаG – простойцикл.
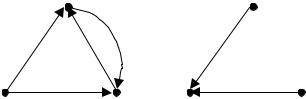
О рграф G′ называетсяобратным к данному орграфу G, еслионимеет тежеверш ины, что иG, адуга( x, y ) принадлежитG′ тогдаитолько тогда, когдадуга( y, x ) принадлежитG. Н арис.3 представленграф G иего дополнение.
y |
y |
x z x z
Рис.3 В графеможно выделить части – подграфы, об ладаю щ иеопределен-
ными свойствами. Рассмотрим граф G = (X,U). G′= (X′,U′) называетсясобственным под граф ом графаG, если Х ′ Х и U′U являю тсясоответственно такими подмножествами X и U, что реб ро (xi, xj) содержится в U′ только в том случае, еслиxi иxj содержатсяв Х ′. Е слиX = Х ′, то такойсоб - ственный подграф называетсяостовным . П орожд енным подграфом графа G намножествеверш инX′ называетсясоб ственныйподграф G′= (X′,U′), такой, что U′ содержитвсетереб раиз U, которыесоединяю тверш ины из X′. Н арис.4 : а) – данный граф G, б ) – остовный подграф, в) – порожденный подграф, г) – соб ственныйподграф.

7
П одграф G′ графаG называется м акси м альным под граф ом по отношени ю кнекотором у свойству P, еслиG′ об ладаетсвойством Р и G′ не являетсясоб ственным подграфом никакого другого подграфа графаG, об - ладаю щ его свойством Р. П одграф G′ графаG называется м и ни м альным под граф ом по отношени ю кнекотором у свойству P, если G′ об ладает свойством Р иникакойподграф графаG, об ладаю щ ийсвойством P, неявляетсясоб ственным подграфом G′. Свойство Р графаG называетсянаслед ственным , есликаждыйподграф графаG об ладаетэтим свойством.
x2
x1
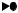 x3
x3
x6 
 x4
x4
x5
а)
x2
x1
 x3
x3
x4
в)
Рис. 4
x2
x1
 x3
x3
x6  x4 x5
x4 x5
б )
x2
x1
 x3
x3
x4
г)
1.2. С Т ЕП ЕННЫ |
Е П О С ЛЕД О В АТ ЕЛЬ НО С Т И |
П усть Г (хi) – множество |
верш ин хj X, для которых в графе G |
сущ ествует дуга(xi ,хj), тогдаэто множество называется окрестностью верш ины хj. И спользуяпонятиеокрестности, граф определяю ткак совокупность множестваверш инимножестваокрестностейв видеG = (X, Г ), гдеГ - неоднозначное отоб ражение, ставящ ее в соответствие каждой верш ине подмножество Г (хi) в Х . Г -1(xi) - множество верш ин xj Х , для которых в графе G сущ ествуетдуга(xi , хj).
Е сли граф ориентированный, то говорят, что дуга(xi, хj) исходитиз верш ины xi и заходитв верш ину хj . Ч исло дуг, которыеимею тверш ину xi своейначальнойверш иной, называю тполустепенью и сх од а верш ины xi и об означаю тd –( xi ). Ч исло дуг, которые имею тверш ину xi своей конечной

|
|
8 |
|
и об означаю тd+(xi ). Заме- |
верш иной, называю тполустепенью зах од а xi |
||||
тим, что d+(xi ) = |Г –1(xi)| , d –(xi ) = | Г ( xi )|. |
|
|
||
¨Упраж нение[6, стр.284]. Д окажите, что |
|
|||
− |
= |
+ |
= m |
d |
å i |
å di |
|||
i X |
x:i |
i X |
x:i |
|
¨Упраж нение[3, стр. 195]. Д окажите, что в б есконтурном графесу- щ ествует, по крайнеймере, однаверш инаснулевойполустепенью заходаи однаверш инаснулевойполустепенью исхода.
Замечание. В ерш инаснулевой полустепенью заходаназывается и с-
точни ком , ас нулевой полустепенью исхода– стоком . Т опологи ческой сорти ровкой б есконтурного графа с одним источником и одним стоком называетсятакаянумерацияверш ин, что длякаждой дуги (i,j) i<j. Т опологическаясортировкаявляетсяосновойнекоторыхалгоритмов об раб откисетевыхграфиков.
Д лянеорграфачисло реб ер, инцидентныхданнойверш инеxi, называетсястепенью (валентностью) верш ины xi иоб означаетсяd(xi). Д ляорграфаd(xi) = d –(xi ) + d+(xi ). Г раф, у которого всеверш ины имею тодну иту же степень, называетсярегулярным (од нород ным ) графом. Е сли степень каждой верш ины равнаr , то граф называется регулярным (од нород ным )
степени r.
¨ Упраж нение [3, стр.12]. Д окажите, что в лю б ом графечисло вер- ш иннечетнойстепеничетно.
¨Упраж нение [3, стр.12]. Д окажите, что суммастепеней верш ин простого графаравнаудвоенному числу реб ер, т.е.
å i d= m2. i X x:i
Замечание 1. Д анное утверждение установлено Э йлером и является историческипервойтеоремойтеорииграфов.
Замечание 2. Разб иением неотрицательного числаn называется конечный наб ор неотрицательных чисел, суммакоторых равнаn. Разби ени е граф а – это представлениечисла2m в видесуммы степенейверш инграфа, что, вооб щ еговоря, невсегдавозможно. Т ак, только дваиз пятиразб иений числа4 (4+0, 3+1, 2+2, 2+1+1, 1+1+1+1) наположительныеслагаемыереализую тсяграфами(рис. 5).
2+1+1 |
1+1+1+1 |
|
|
Рис. 5 |
|
П оследовательность d1 ³ , … |
, ³ dn называется граф и ческой, |
если |
сущ ествует граф G на n верш инахх1, ..., хn такой, что степень |
d(xi) |
|

9
верш ины xi равнаdi длялю б ого i. В этом случаеd = {d1,… ,dn} называется
послед овательностью степеней графаили степенной послед овательно-
стью. И ногда, хотяи редко граф определяетсясвоейстепенной последовательностью однозначно. В об щ ем случаеграфическая последовательность имеетмного реализацийиихчисло определить сложно.
П усть d – правильнаяпоследовательность, т.е. d1 ³ , … , ³ dn. Зафиксируем индексi и через ci об означим остаточную последовательность, которая содержит (n-1) степеней и полученаиз исходной последовательности вычеркиванием i-го члена. П усть, далеепоследовательность di полученаиз последовательностиci в результатеуменьш ениянаединицу каждого из пер-
выхdi членов, тогдаdi называетсяостаточной послед овательностью.
¨Упраж нение [3, стр.157]. Е сли последовательность d графическая, то каждаяостаточнаяпоследовательность di ( = )i)n,также1( являетсяграфической.
Ч тоб ы определить, являетсяли последовательность графической используется, критерий Г авела-Х акими: пусть d – правильнаяпоследовательность, содержащ аяn членов. Е слидлякакого-ниб удь индексаi (1£ i £n) остаточная последовательность di являетсяграфической, то и d - графическаяпоследовательность.
Рассмотрим процедуру (d-процед ура) распознавания графичности последовательностинаосновекритерияГ авела-Х акими:
Шаг 1. П усть {d1 , ... ,dn }- последовательность степеней, упорядоченнаяпо невозрастанию . В ыб ерем произвольноеdi ¹ 0 и исклю чим его из последовательности, приэтом верш ину xi (ведущ аяверш ина) соединим спервымиdi верш инами, несчитаясаму верш ину xi.
Шаг 2. У порядочим по невозрастанию остаточную последователь-
ность.
Шаг 3. Ш аги1-2 выполнять до техпор, поканевозникнетоднаиз следую щ ихситуаций:
а) всечлены остаточной последовательности равны 0. В этом случае последовательность степенейявляетсяграфической. И скомыйграф получается в результате выполнения ш агов, соответствую щ их порядку исклю чениястепеней;
б ) однаиз остаточных степеней отрицательнаэто означает, что по-
следовательность {d1 , ... ,dn} неявляетсяграфической, то есть не сущ ествует простого графа, который ее реализует.
П ри м ер. Рассмотрим последовательность (4, 3, 3, 2, 2). П реоб разова- ниянаосновеd-процедуры приведены в таб лице, представленнойниже.
Т ак как всеостаточныестепениравны 0, то последовательность (4, 3, 3, 2, 2) являетсяграфической. И скомый граф получаетсяв результатевыполненияш агов, соответствую щ ихпорядку изъятиястепеней.
Замечание. В зависимости отвыб ораведущ ихверш инданнаяпроцедураможетстроить различные реализации графической последовательности, в том числеиснекоторымизаданнымисвойствами.

10
Ш |
аг 1 |
x1 |
x2 |
x3 |
x4 |
x5 |
4 |
3 |
3 |
2 |
2 |
||
|
|
3 |
2 |
0 |
1 |
2 |
Ш |
аг 2 |
x1 |
x2 |
x5 |
x4 |
x3 |
3 |
2 |
2 |
1 |
0 |
||
|
|
2 |
1 |
0 |
1 |
0 |
Ш |
аг 3 |
x1 |
x2 |
x4 |
x5 |
x3 |
2 |
1 |
1 |
0 |
0 |
||
|
|
0 |
0 |
0 |
0 |
0 |
Рассмотрим некоторыеутверждения.
♦Упраж нение[6]. П усть d степень верш ины однородного графа. Д о- кажите, что
а) при выполнениеусловияnd = 2m всегдаможно построить соответствую щ ийграф;
б ) длялю б ыхположительныхчиселnd иnd+1, удовлетворяю щ ихусло-
виям
d nd + (d+1) nd+1 = 2m, nd + nd+1 = n,
сущ ествуетсоответствую щ ийграф.
Замечание: В ыражение в а) называется “леммой о рукопожатиях” –
поскольку в каждом рукопожатии участвую тдверуки, то при лю б ом числе рукопожатийоб щ еечисло пожатыхрук четно приусловии, что каждаярука учитываетсястолько раз, в сколькихрукопожатияхонаучаствует.
П ослед овательностью очковтурниранаn верш инахназываетсяпо-
следовательность (s1, s2, … |
, sn), в которой каждоеsi являетсяполустепенью |
||||||||
исходаверш ины турнира. |
|
|
|
|
|
|
|||
♦Упраж нение. [3, стр. 97] Д оказать, что последовательность неотри- |
|||||||||
цательных целых чиселs1, s2, |
… , sn являетсяпоследовательностью очков |
||||||||
турниратогдаитолько тогда, когда |
|
|
|
|
|
||||
n |
− )1 |
nn( |
k |
|
|
− )1 kk( |
|||
а) åsi = |
|
|
; |
б ) длявсех k< n |
åsi |
= |
|
|
. |
2 |
|
2 |
|||||||
i=1 |
|
|
|
i=1 |
|
|
|||
1.3. М АТ РИ Ч НЫ |
Е П РЕД С Т АВ ЛЕНИ Я |
Г РАФ А |
|
||||||
М атри цей см ежности графаG=(X,U) |
(|Х |=n) |
называется матрица |
|||||||
А ={aij}n×n , элементы которойопределяю тсяследую щ им об разом: |
|||||||||
|
aij = |
ì1, |
|
верш ины xiиx j смежнеслыи, |
|
|
|
||
|
í |
|
0, иначе. |
|
|
|
|
|
|
|
|
î |
|
|
|
|
|
|
|
Замечание: В случаекратныхреб ер aij есть количество реб ер, соединяю щ ихверш ины хi и хj. Д ляорграфаaij определяетсякак количество дуг, направленныхотверш ины хi к верш ине хj .
П ри м ер. Г раф G иего матрицасмежностипредставлены нарис.6.
