
Ledeneva_T_M_Algoritmy_teorii_grafov_Kodovye
.pdf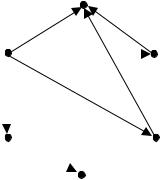
11
|
x2 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
||
|
X1 |
0 |
1 |
0 |
1 |
0 |
1 |
|||
x1 |
||||||||||
X2 |
0 |
0 |
0 |
0 |
0 |
0 |
||||
|
|
x3 |
X3 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|||||||||
|
|
X4 |
0 |
1 |
0 |
0 |
0 |
0 |
||
|
|
|
||||||||
|
|
|
X5 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
|
|
X6 |
0 |
0 |
0 |
0 |
1 |
0 |
|
x6 
 x4
x4
x5 Рис. 6
♦Упраж нение([4], стр. 60; [5], стр. 225; [8], стр. 170) . Д оказать, что дляорграфаG сматрицейсмежностиА (i,j)-ый элементв матрицеА t определяетчисло путейдлины t, ведущ ихиз верш ины xi в xj .
Замечание. М одифицированной матрицей смежности |
~ |
называется |
A |
матрица, у которой вместо 1, об означаю щ ей наличиереб ра, стоитидентификатор этого реб ра. П ри возведении в n степень модифицированной мат-
рицы смежности |
~ |
умножениеб удем рассматривать как конкатенацию – |
A |
приписывание справа к идентификатору, соответствую щ ему i-й строке, идентификатора, соответствую щ его j-му столб цу, суммированиекак об ъ- единениеполученныхв результатеумноженияслов. Д ляопределенияпутей
длины n в орграфе необ ходимо матрицу ~ возвестив степень n.
A
С помощ ью матрицы смежности можно устанавливать различные свойстваграфа. Рассмотрим некоторыеутверждения.
♦Упраж нение. Д оказать, что граф является двудольным тогда и только тогда, когдадля лю б ого нечетного числаn вседиагональные элементы матрицы А n равны 0.
♦Упраж нение([6], стр. 28). Д окажите, что дваграфаявляю тся изоморфными, тогдаи только тогда, когдаихматрицы смежностиполучаю тся друг ихдругаперестановкамистрок истолб цов.
♦Упраж нение([8], стр.171). Д оказать: длятого, чтоб ы n-верш инный граф с матрицей смежности А имелхотя б ы одинконтур, необ ходимо и достаточно, чтоб ы матрица(А 2+А 3 +… +А n) имеланенулевыедиагональные элементы.
♦Упраж нение. Д оказать, что следую щ иесвойстваорграфаэквивалентны:
а) G – б есконтурныйграф;
б ) верш ины орграфаG можно упорядочить таким об разом, что его матрицасмежностиб удетиметь верхнийтреугольныйвид.
Замечание. И з данного утвержденияследует, что б есконтурному графу соответствует треугольнаяматрицасмежности.
12
М атри цей и нци д ентности графаграфаG=(X,U) , |Х |=n , |U|=m на-
зываетсяматрицаB = {bij}n×n , элементы которой определяю тсяследую щ им об разом:
еслиG - орграф
ì |
1, |
верш инаxi - |
если |
дугиu j , |
верш ина |
ï |
- 1, |
верш инаxi - |
если |
дугиu j , |
верш ина |
bij = í |
|||||
ï |
0, |
верш инаxi |
если |
дугеu j , |
инцидентна |
î |
еслиG - неорграф
ì1, |
верш инаxi |
еслиреб ру u j , |
инцидентна |
bij = í |
0, иначе. |
|
|
î |
|
|
Свойстваматрицы инцидентности перечислены в следую щ их утверждениях.
♦Упраж нение[10, стр.147]. В матрицеинцидентности значениелю - б ого минораравно 0, 1 или-1.
♦Упраж нение [10, стр.147]. Ранг матрицы инцидентности произвольного графаравенразностичиславерш иничислакомпонентсвязности.
Замечание. Д лясвязного графасn верш инами ранг матрицы инцидентностиB равен(n-1).
♦Упраж нение. Д оказать, что длялю б ого неорграфаматрицасмежно-
стиА выражается через матрицу инцидентностиВ следую щ им об разом:
А = В В Т - diag[ d1,...,dn ]
где di - степень i-ойверш ины, diag[d1,...,dn] - матрицаразмерности n×n с элементами d1,...,dn наглавнойдиагонали.
1.4. П РЕД С Т АВ ЛЕНИ Е Г РАФ О В В ЭВ М
В ыб ор представления графав Э В М зависит от используемых алгоритмов. Зачастую матрицасмежности является наиб олее удоб ным представлением графа. Д лянеорграфаонаявляетсясимметричной, что позволяетсократить необ ходимыйоб ъем памяти: дляn-верш инного графатреб ует-
|
− |
)1 nn( |
|
ся |
|
|
ячеек. Н едостатком этого представленияявляетсято, что об ычно |
2 |
|
||
|
|
|
|
многиеэлементы матрицы равны 0 ипоэтому б ольш аячасть используемой памяти является лиш ней. К роме того, матрицу смежности удоб но строить по графу, ужезаданному каким-либ о способ ом, но во многихзадачахграф создается динамически, т.е. в ходе реш ения задачи меняю тся множества верш ини (или) реб ер (дуг). В этом случаепредпочтительным являетсяиспользование спи сков см ежности . Д ля задания множестваверш ин, непосредственно достижимыхиз некоторойверш ины x, используетсялинейный однонаправленныйсписок, каждыйэлементкоторого вклю чаетданные(например, некотороечисло) и указатель наследую щ ий элементсписка. Список в целом задаетсяуказателем наего первый элемент, апоследний элементспискасодержитпустой указатель. Задать для верш ины x еесписок смежностиозначаетв произвольном порядкепоместить в данныеэлементов
13
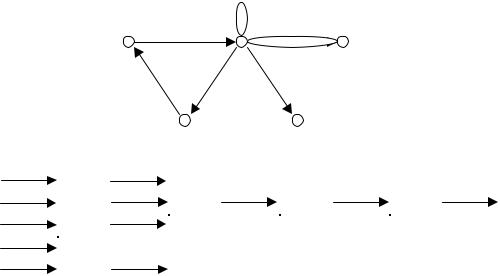
списканомераверш ин, в которыеведутдуги из верш ины x. П ринеоб ходимостисписок смежностиверш инможетдополняться. Д ляэтого в последнем элементесписка“пустой” указатель заменяетсяуказателем надоб авляемый элемент, который становитсяпоследним элементом спискас“пустым” указателем. Е сли количество верш ин орграфаизвестно заранее, то орграф удоб но задавать в виде структуры, называемой м асси вом ли д еров. П од массивом понимаетсяматрица-столб ец, элементамикотороймогутб ыть некоторыеоб ъекты. И хназываю тэлементами массива. Ч исло элементов массивалидеров равно числу верш инграфа, аэлементамимассивалидеров являю тсяпервыеэлементы списков смежности верш инграфа. П ример представления орграфасписками смежности, соб ранными в массив лидеров, представленнарис.7.
|
|
|
|
|
|
|
x1 |
|
|
x2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 |
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
} |
|
|
|
|
|
|
|
|
|
X1 |
∙ |
|
|
X2 |
∙ |
|
|
|
|
|
|
|
|
|
} |
||
X2 |
|
∙ |
|
|
X2 |
∙ |
|
X3 |
∙ |
|
X4 |
∙ |
|
X5 |
∙ |
|
|
X3 |
∙ |
|
|
X1 |
∙ |
|
} |
|
|
|
|
|
|
|
|
|
|
X4 |
∙ |
|
|
} |
|
|
} |
|
|
|
|
|
|
|
|
|
|
X5 |
∙ |
|
|
X2 |
∙ |
|
|
|
|
|
|
|
|
|
|
||
Рис. 7
Н еорграф задать спомощ ью списков смежности можно так же, как и орграф. В список смежности верш ины x войдут всеверш ины, смежные с ней, асписки смежности могутб ыть соб раны в массив лидеров. Н есмотря нато, что представлениеграфав видематрицы инцидентностииграетвесьмаб ольш ую роль в теоретическихисследованиях, практически этотспособ весьманеэффективен. П режде всего, в матрице в каждом столб це только дваненулевых элемента, что делаетэтот способ представления графанеэкономным приб ольш ом количествеверш ин. К рометого, реш ениепрактических задач спомощ ью матрицы инцидентности весьматрудоемко. В озможно представление графас помощ ью кодов и сущ ествую т алгоритмы, ориентированныенатакоепредставление.
З АД АЧ И И У П РАЖ НЕНИ Я
1. И зоб разитеграфически следую щ иеграфы: а) G1 = ({a,b,c}, {(a,b),
(a,c), (a,a), (b,c)}); б ) G2 = ({x1, x2, x3, x4},{(x1, x2),(x1, x4), (x2, x4),(x3, x3) (x3, x4),(x4, x1)}).
14
2.Н арисовать граф, представляю щ ийследую щ ую игру: б росаетсямонетадо техпор, поканевыпадетдважды герб илиреш ка. Е слисначаладва разавыпадетгерб , поб еждаетигрок 1, в противном случаеигрок 2.
3.Сколько сущ ествуетнеорграфов сn верш инами?
4.Д оказать, что граф Kn имеетn(n-1)/2 реб ер.
5.Сколько реб ер имеетграф Km,n?
6.П оказать, что в полном неорграфе Kn каждоереб ро принадлежит
ровно (n-2) треугольникам, то есть циклам длины 3. О б ратноеневерно.
7.Н айдитевыражениедлячислареб ер графаL(G) через степенивер-
шинграфаG.
8.Д оказать, что изоморфизм графов представляетсоб ой отнош ение эквивалентности.
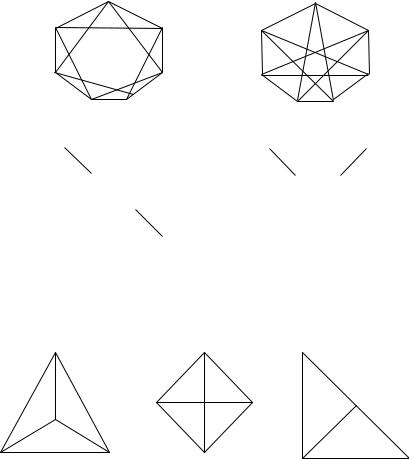
9.П оказать, что графы, изоб раженныенарисунках7а), 7б ), изоморфны, ана7в) и7г) - неизоморфны.
|
а) |
|
|
б ) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) г) Рис. 7
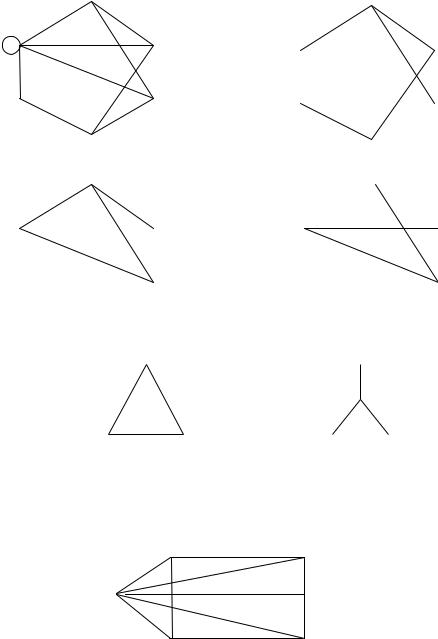
10. Г рафы, изоб раженныенарис. 8а) и8б ) изоморфны, но онинеизоморфны графу нарис. 8в). П очему?
а) |
б ) |
в) |
Рис. 8
11.П ривестипример простого графа, изоморфного реб ерному.
12.П редложитеалгоритм проверки заданного множествареб ер неорграфанато, являетсялионо цепью .
15
13.П риведитепримеры (когдаэто возможно): а) двудольного графа, являю щ егосярегулярным; б ) платоноваграфа, являю щ егосядвудольным.
14.Д ляданного графаG определить типы подграфов
|
|
х2 |
|
х2 |
||
|
х1 |
х3 |
х1 |
|
х3 |
|
|
|
|
|
|
||
|
|
|
G |
|
|
G 1 |
х6 |
|
х4 |
х6 |
|
х4 |
|
|
|
х5 |
|
х5 |
||
|
|
х2 |
|
х2 |
||
|
х1 |
х3 |
х1 |
|
х3 |
|
|
|
|
|
|
||
|
|
|
G 2 |
|
|
G 3 |
|
|
х4 |
Рис.9 |
х4 |
||
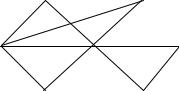
15. П оказать, что реб ерные графы графов, изоб раженных нарис.10, изоморфны.
Рис.10 16. Д ляграфа, изоб раженного нарис.11, построить а) остовный под-
граф G=(X,U), где(x, y) U, если d(x)+d(y) - четноечисло; б ) подграф, не являю щ ийсяпорожденным.
Рис.11
17. Д ля графа, изоб раженного нарис.12, описать: а) порожденный подграф намножествеверш ин{x1, x4, x5}; б ) остовный подграф (X,Y), где
(xi, xj) Y тогдаи только тогда, когда(i+j ) - простоечисло; |
в) остовный |
подграф подграфаиз а), определенный так же как в б ). |
|
18. В осстановить граф G по его подграфам Gi=G-Vi |
, где G1=K4-x, |
G2=P3 K1 , G3=K1,3 , G4=G5=K1,3+x . |
|
|
16 |
|
19. Д ля графа, изоб раженного нарис.12, определить d+(xi), d-(xi), |
||
Г 2(x2), Г 2(x1). |
|
|
x 1 |
|
x2 |
x 6 |
|
x 3 |
|
||
x 5 |
x4 |
|
Рис. 12 20. П остроить граф (если онсущ ествует) споследовательностью сте-
пеней: а) (4, 3, 3, 2, 2); б ) (5, 4, 2, 2, 1); в) (3,3,2); г) (3,2,2,1).
21.П остройтеорграф, длякоторого последовательность (3,3,3,2,2) являетсякак списком полустепенейисходаверш ин, так исписком полустепенейзахода.
22.Н арисовать граф, имею щ ийразб иение5+5+3+3+2+2.
23. П окажите, что простойграф, имею щ ий, по крайнеймере, двевер-
шины, содержитдвеверш ины одинаковойстепени.
24.Д окажите, что несущ ествуетнеорграфа, степенивсехверш инкоторого попарно различны.
25.Д окажите, что если в орграфеG отсутствую тверш ины снулевой
полустепенью исхода(захода), то в G имеетсяпростойконтур.
26.О характеризовать матрицы смежности полных графов, двудольныхграфов. Ч то можно сказать о матрицесмежностипростого графаи его дополнения?
27.П усть матрицасмежностиграфаG имеетб лочную структуру
|
éА 1 |
0 |
ù ... |
||
|
ê |
|
А 2 ... |
ú |
|
А = |
ê |
|
ú |
, |
|
|
... |
||||
|
ê |
|
ú |
|
|
|
ê |
0 |
|
ú |
|
|
ë |
А n û |
|
||
гдекаждое А i являетсяквадратнойматрицейсб улевымиэлементами, авсе остальные элементы равны 0. Ч то можно сказать о свойствах соответствую щ его графа?
28. П усть симметричнаяматрицаА порядкаn, в каждой строкекоторойнаходитсяодинаковоенечетноечисло k ненулевыхэлементов, является матрицейсмежностинеорграфа. П оказать, что число верш инграфаn четное
(аii=0).
29.Д оказать, что еслинеорграф k-регулярный, то число k есть соб ственноечисло матрицы смежностиграфа.
30.Н айтиспомощ ью матрицы смежностиd-(xi) иd+(xi)
|
17 |
1 |
|
21 |
0 |
æ |
|
ö |
|||
ç |
|
0 |
÷ |
12 |
0 |
ç |
|
÷ |
|||
A = ç |
0 |
01 |
÷ . |
1 |
|
ç |
÷ |
|
|||
ç |
1 |
10 |
÷ |
0 |
|
è |
ø |
|
31. П усть Gn - граф смножеством верш ин{х1,...,хn}, в котором верш и- ны хi ихj смежны тогдаитолько тогда, когдаi иj взаимно просты. И зоб разитеграфы G4 и G8 и найдитеихматрицы смежности. П окажите, что, если m<n, то Gm являетсяподграфом графаGn.
32. Ч ему равнасуммачисел, стоящ ихв лю б ой из строк матрицы инцидентности В ? Ч то можно сказать о сумме чисел, стоящ их в лю б ом из столб цов?
34.П окажите, что лю б аястрокаматрицы В являетсялинейнойкомб и- нациейостальныхстрок.
35.Д лялю б ого неорграфаможно определить матрицу соседствареб ер
С=[cij]nn, |
в которой cij=1, еслиi-оеиj-оереб раинцидентны с об щ ей вер- |
ш иной |
и cij=0 в противном случае. cii=0. К ак можно выразить матрицу С |
через матрицу инцидентности? |
|
36. Н аписать процедуру перехода между лю б ыми двумяспособ ами маш инного представленияграфа(А , В , список смежности).
2. Д О С Т И Ж И М О С Т Ь И С В Я З НО С Т Ь
Е сли для лю б ой пары верш инсущ ествуетцепь их соединяю щ ая, то такойграф называетсясвязным , иначеграф называетсянесвязным .
♦Упраж нение ([6], стр. 24). Д окажите, что лю б ойграф либ о сам связен, либ о его дополнение.
П равильная графическая последовательность d можетб ыть реализованасвязным графом тогдаитолько тогда, когдаdn>0 иверно неравенство
n |
|
|
. |
å i |
³ |
- |
|
i=1 |
)1d n( 2 |
||
|
|
|
|
Е слиуказанныеусловиявыполняю тся, то d-процедура, накаждом ш а- |
|||
гекоторойведущ ейявляетсяверш инасминимальнойположительнойостаточнойстепенью , приводитк связному графу.
Д ля орграфов понятие связности является б олее содержательным. М ожно выделить три типасвязности орграфа. О рграф называется слабо связным , если его основаниеесть связный граф; од ностороннесвязным , если длялю б ыхдвухразличныхверш инxi и xj сущ ествует, по крайнеймере, одинпуть из xi в xj илииз xj в xi ; си льно связным , еслидлялю б ых двухразличныхверш инxi иxj сущ ествуетпуть из xi в xj иоб ратно.
Е слив графеG сущ ествуетпуть, идущ ийотверш ины xi к верш инеxj,
то говорят, что верш инаxj д ости жи м а |
из верш ины xi . Т аким об разом, орг- |
|
раф является односторонне связным, |
если для каждой пары верш ин |
|
выполняется условие: xi достижимаиз xj |
или наоб орот; орграф является |
|
сильно связным, если xi достижимаиз xj |
и наоб орот, т.е. верш ины xi и xj |
|
являю тсявзаимно достижимыми. |
|
|
18
Ч тоб ы определить, каким типом связности об ладает данный граф можно использовать следую щ иепризнаки.
¨Упраж нение([4], стр. 62). П усть I – матрица, состоящ аяиз 1; б улевафункцияВ : N®{0,1}, такаячто
ì0, если =x , 0 )Bx(= í
î1, если >x , 0
переводитпроизвольную неотрицательную матрицу в матрицу сэлементамииз {0,1}. Д оказать, что орграф G сматрицейдостижимостиR иматрицей смежностиА :
а) G сильно связентогдаитолько тогда, когдаR = I, где
б ) G одностороннесвязентогдаитолько тогда, когда
B(R+R¢) = I,
гдеR¢ - матрица, транспонированнаяк R;
в) G слаб о связентогдаитолько тогда, когда
B[(I+A+A¢)n-1] = I,
где n –число верш инв G; А ¢ - матрица, транспонированнаяк А . Свойство связности является наследственным, т.е. в данном графе
можно рассматривать подграфы, об ладаю щ ие теми же типами связности, что иисходныйграф. П усть свойство Р – это типсвязности. М аксимальный связный подграф графаG называется ком понентой связности . К аждый граф представляется в виде дизъю нктивного об ъединения своих связных компонент. Разложение графанасвязные компоненты определено однозначно. А налогично, од носторонняя ком понента представляетсоб ой одностороннесвязный максимальный подграф, аси льная ком понента (СК ) максимальныйсильно связныйподграф графаG. И начесильнаякомпонента графаназываетсябиком понент ой, поскольку онасостоитиз верш ин, которые являю тся взаимно достижимыми. И з определений следует, что односторонниекомпоненты графамогутиметь об щ иеверш ины, сильнаякомпонентадолжнасодержаться, по крайнеймере, в однойодностороннейкомпоненте, аодносторонняякомпонентасодержитсяв некоторой слаб ойкомпонентеданного графаG. О чевидно, что всякий сильно связный граф одновременно является одностороннесвязным и слаб о связным. В сякий одностороннесвязный граф в то жевремяявляетсяи слаб о связным. О б ратные утвержденияневерны.
¨Упраж нение([4], стр. 52). Д оказать, что в орграфекаждаяверш ина входитв одну итолько в одну сильную компоненту.
П усть S = {S1, S2, … , Sp} – множество сильных компонент графа G=(X,U). Г раф G*=(S,US) называетсяконд енсаци ей графа, есликаждаяего верш инаSiÎS соответствуетсильнойкомпонентеграфаG, а(Si,Sj)ÎUS тогда итолько тогда, когдав G сущ ествует (x,y)ÎU, причем x ÎSi , yÎSj.
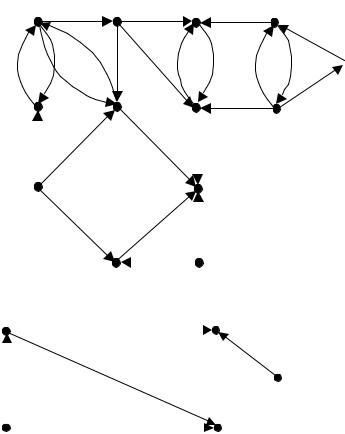
Н арис.1 представленграф G исоответствую щ аяему конденсация. ¨Упраж нение([4], стр. 54; [6], стр. 283). Д оказать, что конденсация
G* орграфаG неимеетконтуров.
19
Рассмотрим задачу определения сильных компонент графа. В ведем некоторыедополнительныеопределения.
М атри цей д ости жи м ости графаG=( X,U ), | X |=n называетсяматри-
цаR = {rij }n×n , элементы которойопределяю тсяследую щ им об разом:
r |
ì1, |
верш инаx |
i |
если верш ины x |
j |
, |
из |
достижима |
= í |
|
0, иначе |
|
|
|
|||
ij |
î |
|
|
|
|
|
|
Заметим, что всякая верш инадостижимасамаиз себ я, поэтому rii = 1длявсехi.
x |
x6 |
x |
x11 |
1 |
10 |
|
 x13
x13
|
x2 |
|
|
|
|
|
|
|
|
|
x8 |
|
|
|
x12 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x5 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1* = { |
|
|
|
|
, x6 }, xy51 x2 x |
* = { y , x }x |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
8 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* = { |
, |
, x x}x |
x |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
13 |
12 |
|
|
|
|
|
|
|
|
|
|
|
* = { |
|
|
|
, xy} x |
|
|
|
||||
x* = {x |
5 |
} |
|
|
|
|
|
|
4 |
, x |
7 |
|
|
|
|||||||
5 |
|
|
|
|
|
|
|
|
|
|
3 |
|
9 |
|
|
|
|
||||
Рис. 1
М атри цей контрд ости жи м ости графаG = ( X, U ), | X | = n называет- |
|
||||
сяматрицаQ = {qij }n×n , элементы которой определяю тсяследую щ им об ра- |
|
||||
зом: |
|
|
|
|
|
ì1, |
верш инаx j |
если |
верш ины xi , |
из |
достижима |
qij = í |
|
0, иначе |
|
|
|
î |
|
|
|
|
|
М ножество д ости жи м ости верш ины xi |
R(xi), состоящ ее из таких |
||||
верш инxj , длякоторыхrij=1, определяетсяформулой: |
|
|
|||
R(xi) = { xi |
} Г (xi) Г 2(xi) ... Г р(xi) , где р ≤ n. |
|
|
||
♦Упраж нение. |
П усть орграф G имеетматрицу достижимости R и R2 |
|
|||
= S = {sij}n×n. Д оказать, что
20
а) сильнаякомпонента, содержащ ая верш ину xi, определяетсяединичными элементами в i-й строке(или i-ом столб це) поэлементного произведенияR×Q;
б ) число верш инв сильнойкомпоненте, содержащ ейxi, равно sii.
М ножество контрд ости жи м ости верш ины xi Q(xi) состоитиз таких верш инxj , длякоторыхqij=1, иопределяетсяформулой:
Q(xi) = { xi } Г -1(xi) Г -2(xi) ... Г -p(xi) , где р ≤ n.
Замечание. Т ак как граф G являетсясвязным, если лю б аяпаравер- ш инсоединенацепью , то очевидно, что дляпроверки связностиграфадостаточно построить множество достижимости или контрдостижимости для произвольнойверш ины х0. Е слиR(x0) = X (илиQ(x0) = X), то граф является связным.
М атрицадостижимости несеточень важную информацию об ориентированном графе. Е еанализ позволяетнайтисильныекомпоненты графа, в которые входятвзаимно достижимые верш ины. Д ля двух таких верш инс номерами i и j должно выполнятьсяравенство rij = rji = 1. П оэтому, чтоб ы найти сильную компоненту, в которую входитi-яверш инаорграфа, нужно просмотреть i-ю строку иi-йстолб ец матрицы R исформировать множество Pi = {j: rij = rji = 1} номеров верш ин, порождаю щ ихискомую сильную компоненту. И з определенияматрицы достижимости вытекает, что в Pi содержатсяномеравсехверш инданнойсильнойкомпоненты. П оскольку дверазличные сильные компоненты не пересекаю тся, верш ины с номерами их множестваPi при поискедругихсильныхкомпонентможно исклю чить из рассмотрения. П роцесс поисканачинается спроизвольной верш ины и заканчивается, когдадля каждой верш ины б удет найденасодержащ ая ее сильнаякомпонента. М ожетоказаться, что некоторые(аможетб ыть ивсе) сильныекомпоненты содержаттолько по однойверш ине, поскольку каждая верш ина, по определению , достижимасамаиз себ я.
П ри м ер. П усть матрицадостижимостиграфаимеетвид
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
R = |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
В соответствиисописанной выш епроцедуройпоиск сильныхкомпо- |
||||||||
нентприведетк следую щ им результатам: Р1 |
= {x1}, P2 = {x2, x3}, P3 = {x4, |
|||||||
x5}, P4 = {x6, x7}.
Рассмотрим другиеалгоритмы.
а) алгор ит м н ахож ден ия сильн ы х к ом пон ен т гр афа н а осн ове м ат р иц дост иж им ост и и к он т р дост иж им ост и:
