Introduction to Python for Science, Release 0.9.23

9.3.2 Solving systems of nonlinear equations

Solving systems of nonlinear equations is not for the faint of heart. It is a difficult problem that lacks any general purpose solutions. Nevertheless, SciPy provides quite an assortment of numerical solvers for nonlinear systems of equations. However, because of the complexity and subtleties of this class of problems, we do not discuss their use here.

9.4 Solving ODEs

The scipy.integrate library has two powerful powerful routines, ode and odeint, for numerically solving systems of coupled first order ordinary differential equations (ODEs). While ode is more versatile, odeint (ODE integrator) has a simpler Python interface works very well for most problems. It can handle both stiff and non-stiff problems. Here we provide an introduction to odeint.

A typical problem is to solve a second or higher order ODE for a given set of initial conditions. Here we illustrate using odeint to solve the equation for a driven damped pendulum. The equation of motion for the angle that the pendulum makes with the vertical is given by

where t is time, Q is the quality factor, d is the forcing amplitude, and is the driving frequency of the forcing. Reduced variables have been used such that the natural (angular) frequency of oscillation is 1. The ODE is nonlinear owing to the sin term. Of course, it’s precisely because there are no general methods for solving nonlinear ODEs that one employs numerical techniques, so it seems appropriate that we illustrate the method with a nonlinear ODE.

The first step is always to transform any nth-order ODE into a system of n first order ODEs of the form:

Introduction to Python for Science, Release 0.9.23

We also need n initial conditions, one for each variable yi. Here we have a second order ODE so we will have two coupled ODEs and two initial conditions.

We start by transforming our second order ODE into two coupled first order ODEs. The transformation is easily accomplished by defining a new variable ! d =dt. With this definition, we can rewrite our second order ODE as two coupled first order ODEs:

ddt = !

d!dt = Q1 ! + sin + d cos t :

In this case the functions on the right hand side of the equations are

f1(t; ; !) = !

1

f2(t; ; !) = Q ! + sin + d cos t :

Note that there are no explicit derivatives on the right hand side of the functions fi; they are all functions of t and the various yi, in this case and !.

The initial conditions specify the values of and ! at t = 0.

SciPy’s ODE solver scipy.integrate.odeint has three required arguments and many optional keyword arguments, of which we only need one, args, for this example. So in this case, odeint has the form

odeint(func, y0, t, args=())

The first argument func is the name of a Python function that returns a list of values of the n functions fi(t; y1; :::; yn) at a given time t. The second argument y0 is an array (or list) of the values of the initial conditions of y1; :::; yn). The third argument is the array of times at which you want odeint to return the values of y1; :::; yn). The keyword argument args is a tuple that is used to pass parameters (besides y0 and t) that are needed to evaluate func. Our example should make all of this clear.

After having written the nth-order ODE as a system of n first-order ODEs, the next task is to write the function func. The function func should have three arguments: (1) the list (or array) of current y values, the current time t, and a list of any other parameters params needed to evaluate func. The function func returns the values of the derivatives dyi=dt = fi(t; y1; :::; yn) in a list (or array). Lines 5-11 illustrate how to write func for our example of a driven damped pendulum. Here we name the function simply f, which is the name that appears in the call to odeint in line 33 below.

The only other tasks remaining are to define the parameters needed in the function, bundling them into a list (see line 22 below), and to define the initial conditions, and

Introduction to Python for Science, Release 0.9.23

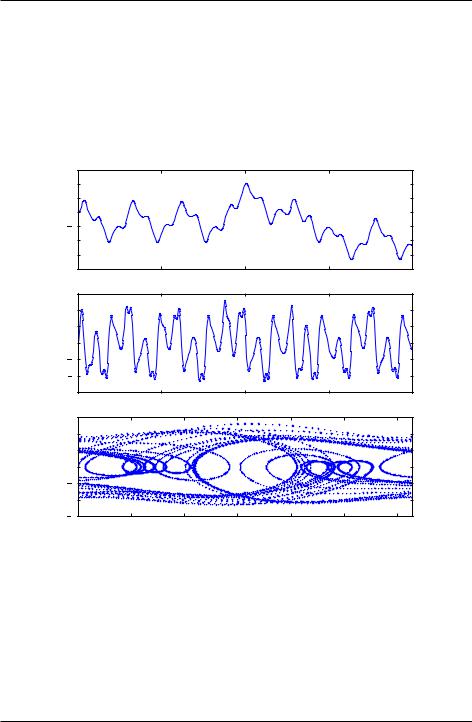
bundling them into another list (see line 25 below). After defining the time array in lines 28-30, the only remaining task is to call odeint with the appropriate arguments and a variable, psoln in this case‘‘ to store output. The output psoln is an n element array where each element is itself an array corresponding the the values of yi for each time in the time t array that was an argument of odeint. For this example, the first element psoln[:,0] is the y0 or theta array, and the second element psoln[:,1] is the y1 or omega array. The remainder of the code simply plots out the results in different formats. The resulting plots are shown in the figure Pendulum trajectory after the code.

1import numpy as np

2import matplotlib.pyplot as plt

3from scipy.integrate import odeint

4

5def f(y, t, params):

6theta, omega = y # unpack current values of y

7 Q, d, Omega = params # unpack parameters

8derivs = [omega, # list of dy/dt=f functions

11

12# Parameters

13Q = 2.0 # quality factor (inverse damping)

14d = 1.5 # forcing amplitude

15Omega = 0.65 # drive frequency

16

17# Initial values

18theta0 = 0.0 # initial angular displacement

19omega0 = 0.0 # initial angular velocity

20

21# Bundle parameters for ODE solver

22params = [Q, d, Omega]

23

24# Bundle initial conditions for ODE solver

25y0 = [theta0, omega0]

26

27# Make time array for solution

28tStop = 200.

29tInc = 0.05

30t = np.arange(0., tStop, tInc)

31

32# Call the ODE solver

33psoln = odeint(f, y0, t, args=(params,))

34

35# Plot results

36fig = plt.figure(1, figsize=(8,8))

Introduction to Python for Science, Release 0.9.23

37

38# Plot theta as a function of time

39ax1 = fig.add_subplot(311)

40ax1.plot(t, psoln[:,0])

41ax1.set_xlabel(’time’)

42ax1.set_ylabel(’theta’)

43

44# Plot omega as a function of time

45ax2 = fig.add_subplot(312)

46ax2.plot(t, psoln[:,1])

47ax2.set_xlabel(’time’)

48ax2.set_ylabel(’omega’)

49

50# Plot omega vs theta

51ax3 = fig.add_subplot(313)

52twopi = 2.0*np.pi

53ax3.plot(psoln[:,0]%twopi, psoln[:,1], ’.’, ms=1)

54ax3.set_xlabel(’theta’)

55ax3.set_ylabel(’omega’)

56ax3.set_xlim(0., twopi)

57

58plt.tight_layout()

59plt.show()

The plots above reveal that for the particular set of input parameters chosen Q = 2.0, d = 1.5, and Omega = 0.65, the pendulum trajectories are chaotic. Weaker forcing (smaller d) leads to what is perhaps the more familiar behavior of sinusoidal oscillations with a fixed frequency which, at long times, is equal to the driving frequency.

9.5 Discrete (fast) Fourier transforms

The SciPy library has a number of routines for performing discrete Fourier transforms. Before delving into them, we provide a brief review of Fourier transforms and discrete Fourier transforms.

9.5.1 Continuous and discrete Fourier transforms

The Fourier transform of a function g(t) is given by

Introduction to Python for Science, Release 0.9.23

Figure 9.3: Pendulum trajectory

Introduction to Python for Science, Release 0.9.23

Here we define the Fourier transform in terms of the frequency f rather than the angular frequency ! = 2 f.

The conventional Fourier transform is defined for continuous functions, or at least for functions that are dense and thus have an infinite number of data points. When doing numerical analysis, however, you work with discrete data sets, that is, data sets defined for a finite number of points. The discrete Fourier transform (DFT) is defined for a function gn consisting of a set of N discrete data points. Those N data points must be defined at equally-spaced times tn = n t where t is the time between successive data points and n runs from 0 to N 1. The discrete Fourier transform (DFT) of gn is defined as

N 1

X

where l runs from 0 to N 1. The inverse discrete Fourier transform (iDFT) is defined as

The DFT is usually implemented on computers using the well-known Fast Fourier Transform (FFT) algorithm, generally credited to Cooley and Tukey who developed it at AT&T Bell Laboratories during the 1960s. But their algorithm is essentially one of many independent rediscoveries of the basic algorithm dating back to Gauss who described it as early as 1805.

9.5.2 The SciPy FFT library

The SciPy library scipy.fftpack has routines that implement a souped-up version of the FFT algorithm along with many ancillary routines that support working with DFTs. The basic FFT routine in scipy.fftpack is appropriately named fft. The program below illustrates its use, along with the plots that follow.

import numpy as np

from scipy import fftpack import matplotlib.pyplot as plt

Introduction to Python for Science, Release 0.9.23

fig = plt.figure(1, figsize=(8,6), frameon=False) ax1 = fig.add_subplot(211)

ax1.plot(t, g) ax1.set_xlabel(’t’) ax1.set_ylabel(’g(t)’)

ax2 = fig.add_subplot(212)

ax2.plot(f, np.real(G), color=’dodgerblue’, label=’real part’) ax2.plot(f, np.imag(G), color=’coral’, label=’imaginary part’) ax2.legend()

ax2.set_xlabel(’f’) ax2.set_ylabel(’G(f)’)

plt.show()

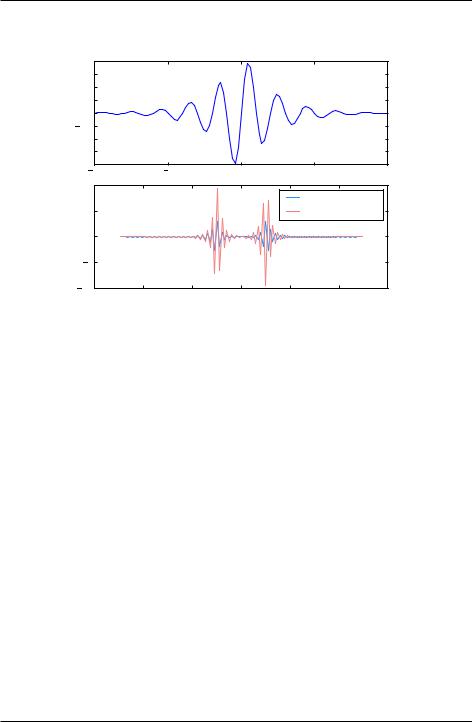
The DFT has real and imaginary parts, both of which are plotted in the figure.

The fft function returns the N Fourier components of Gn starting with the zerofrequency component G0 and progressing to the maximum positive frequency component G(N=2) 1 (or G(N 1)=2 if N is odd). From there, fft returns the maximum negative component GN=2 (or G(N 1)=2 if N is odd) and continues upward in frequency until it reaches the minimum negative frequency component GN 1. This is the standard way that DFTs are ordered by most numerical DFT packages. The scipy.fftpack function fftfreq creates the array of frequencies in this non-intuitive order such that f[n] in the above routine is the correct frequency for the Fourier component G[n]. The arguments of fftfreq are the size of the the orignal array g and the keyword argument d that is the spacing between the (equally spaced) elements of the time array (d=1 if left unspecified). The package scipy.fftpack provides the convenience function fftshift that reorders the frequency array so that the zero-frequency occurs at the middle of the array, that is, so the frequencies proceed monotonically from smallest (most

Introduction to Python for Science, Release 0.9.23

Figure 9.4: Function g(t) and its DFT G(f).

negative) to largest (most positive). Applying fftshift to both f and G puts the frequencies f in ascending order and shifts G so that the frequency of G[n] is given by the shifted f[n].

The scipy.fftpack module also contains routines for performing 2-dimensional and n-dimensional DFTs, named fft2 and fftn, respectively, using the FFT algorithm.

As for most FFT routines, the scipy.fftpack FFT routines are most efficient if N is a power of 2. Nevertheless, the FFT routines are able to handle data sets where N is not a power of 2.

scipy.fftpack also supplies an inverse DFT function ifft. It is written to act on the unshifted FFT so take care! Note also that ifft returns a complex array. Because of machine roundoff error, the imaginary part of the function returned by ifft will, in general, be very near zero but not exactly zero even when the original function is a purely real function.