Правило трапеций

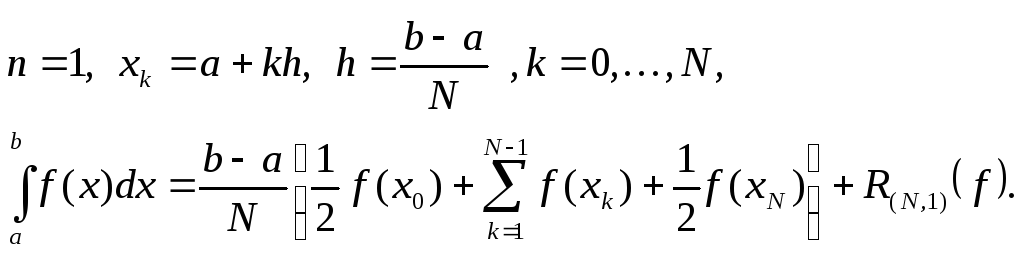
Если , то

Правило Симпсона (парабол)

Если , то

Замечание 5.Алгоритмы численного интегрирования, построенные на основе локально-интерполяционных квадратурных формул (25) имеют существенный недостаток – они насыщаемые. Насыщаемость проявляется в том, что асимптотическое представление погрешности формулы (25) имеет главный член. Отсюда следует неулучшаемость оценки погрешности, сколь бы ни была гладкой функция.

В зависимости от гладкости функции можно выписать любое заданное число членов асимптотического ряда, в который разлагается погрешность. Рассмотрим конкретный пример – правило трапеций. Если, то для погрешности квадратурной формулыимеет место представление

где ине зависит от. Из (28) и следует насыщаемость правила трапеций. Классом насыщения в данном случае является пространство.

Имеются простые способы преодоления дефекта локально интерполяционных квадратурных формул – их насыщаемости. Все они основаны на простом соображении, что у соответствующей линейной комбинации двух значений составной квадратурной формулы с различными, но кратными шагами, главный член погрешности исключается. Например, для правила трапеций в силу (28) , и мы получаем повышение порядка точности, если возьмем линейную комбинацию значений формулы для числа узловисоответственно с коэффициентами 1 и – 4.

Пусть погрешность локально-интерполяционной квадратурной формулы (25) представима в виде

где и константане зависит от. Тогда

Отсюда получаем

и, следовательно, с точностью до имеем

Если , то

Вычисление приближенной оценки погрешности по формуле (29) называется правилом Рунге.

Число

в (30) называется уточненным (экстраполированным) по Ричардсонуприближенным значением интеграла(с погрешностью).

Замечание 6.Используя этот прием, можно уничтожить и следующие члены асимптотического разложения погрешности квадратурной формулы. Однако целесообразнее применять квадратурные формулы, сразу приводящие к ненасыщаемым алгоритмам, например, составные формулы Гаусса. Отметим, что составные квадратурные формулы, основанные на формулах Гаусса с достаточно большим числом узлов, дают хорошие результаты как для очень гладких функций, так и для функций невыской гладкости.

Замечание 7. Каждая квадратурная формула рассчитывается на определенную гладкость подинтегральной функции. Например, для правила Симпсона погрешность, если. Если квадратурная формула имеет алгебраический порядок точности, то при ее применении можно рассчитывать получить «малую погрешность» только в том случае, когдаимеет непрерывные производные до порядка, не меньшего. В противном случае погрешность вычисления интеграла может оказаться большой. Для увеличения порядка гладкости подинтегральную функциюпредставляют в виде двух слагаемых

которые выбирают так, чтобы: содержала все особенностиили их главную часть ивычислялся точно;должна иметь непрерывные производные порядка, большего, для того, чтобы интегралможно было вычислить с достаточной точностью с помощью выбранной квадратурной формулы. Приемы разложения (32) для конкретных классов подинтегральных функций изложены в[3].

1.8. Задание. Вычислить интегралс точностью, используя правило Симпсона и составную квадратурную формулу Гаусса с пятью узлами. Оценить погрешность используемых квадратурных формул и определить число частичных отрезков разбиения, необходимое для достижения заданной точности вычисления интеграла.

Замечание 8.Обычно для вычисления интегралас точностьюиспользуют итерационный процесс с последовательным удвоением числачастичных отрезков разбиения.

Если , то условием останова процесса является выполнение неравенства

при этом интеграл вычисляется по формуле (31).