Для любой таблицы узлов :, используя формулу (8), получаем

где - константа Лебега.

Замечание 3. При любом выборе узлов интерполяции имеет место (см.[4], стр. 118) неравенство С.Н.Бернштейна Введем оператор, преобразующий функциюв интерполяционный многочлен Лагранжа. Оператор- линейный и ограниченный. Нетрудно показать, что. Из неравенства С.Н.Бернштейна и теоремы Банаха-Штейнгауса немедленно следует, что для любой таблицы узлов интерполяции:найдется такая функция, для которой последовательность интерполяционных многочленовнеограниченно расходится.

Замечание 4. Расходимость интерполяционного процесса может вызвать осложнения в задаче вычисления интеграла. При неудачном выборе узлов квадратурный процесс (5), порожденный квадратурной формулой (7)–(8), будет расходящимся (сумма может неограниченно расти).

1.4. Квадратурные формулы Ньютона-Котеса

Возьмем на отрезке равноотстоящие узлыи построим интерполяционную квадратурную формулу (см. (7)-(8))

где

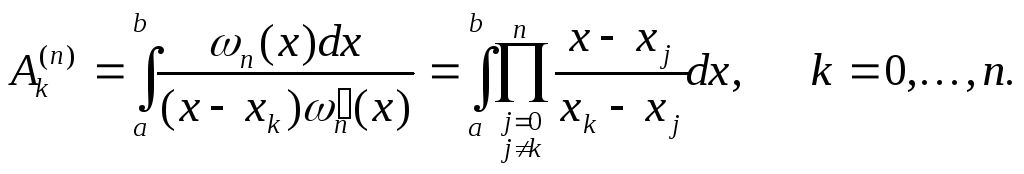
Сделав в интеграле замену переменного , получим

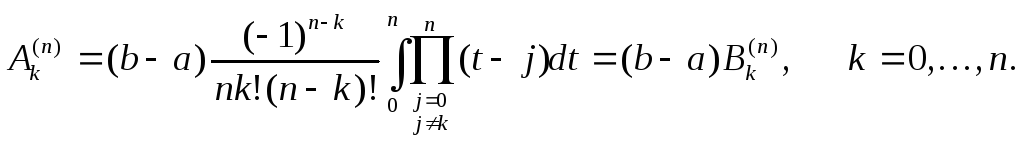
Здесь коэффициенты

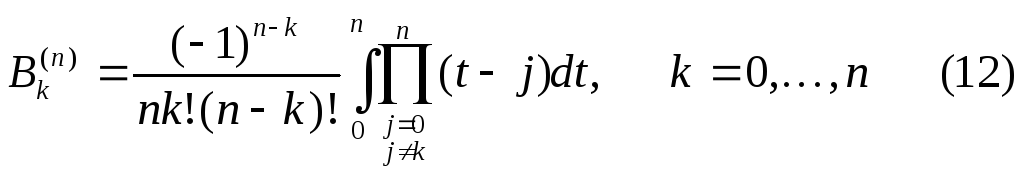
не зависят от промежутка интегрирования и могут быть вычислены заранее.

Интерполяционная квадратурная формула с равноотстоящими узлами и коэффициентами , вычисленными по формуле (12),

называется квадратурной формулой Ньютона-Котеса.

Коэффициенты длявычислены и содержатся в справочниках по численному интегрированию (см.[3], стр. 16-19). Приведем значениядля малых:

Квадратурная формула Ньютона-Котеса точна на константах: . Длявсе коэффициентыположительны. Привстречаются три отрицательных коэффициента, а привсе коэффициенты положительны. Длясредибудут отрицательные. Причем имеет место, как показал Д.Пойа, соотношение

Более того, абсолютные величины будут довольно быстро расти придля любого фиксированного. Это означает, что квадратурный процесс, порожденный квадратурными формулами Ньютона-Котеса (13), является расходящимся (не выполняется условие 2) теоремы 2). Поэтому в приложениях применяются формулы Ньютона-Котеса при небольших значениях().

Если число узлов в формуле Ньютона-Котеса (13) нечетное, то алгебраический порядок точности формулы равени дляпогрешность представима в виде

где ,и множительотрицателен.

Если же число узлов в формуле Ньютона-Котеса (13) четное, то алгебраический порядок точности формулы равени дляпогрешность представима в виде

здесь ,и множительотрицателен.

Приведем наиболее распространенные формулы Ньютона-Котеса:

Формула трапеций

Если , то.

Формула Симпсона (парабол)

Если , то

Формула трех восьмых

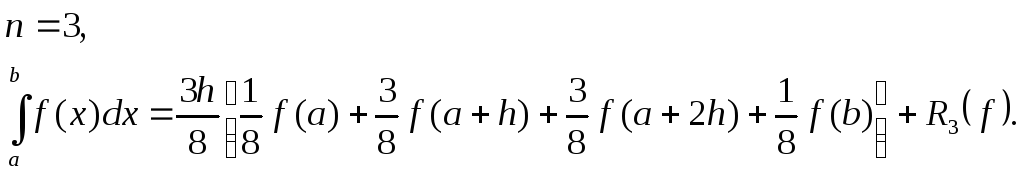
Если , то

1.5. Квадратурные формулы Гаусса

Пусть требуется построить квадратурную формулу сузлами, имеющую максимально возможный алгебраический порядок точности. Нужно определитьпараметра квадратурной формулы: узлыи коэффициенты.

Ясно, что наивысший алгебраический порядок точности квадратурной формулы с узлами не может быть выше, чем. Действительно, возьмем многочленстепени. Тогданои, следовательно, погрешность квадратурной формулы.

Теперь мы можем попытаться построить квадратурную формулу с алгебраическим порядком точности .

Теорема 3.Для того чтобы квадратурная формула (2) с узламиимела алгебраический порядок точности, необходимо и достаточно, чтобы многочленстепенибыл ортогонален налюбому многочленустепени меньшей или равной, то есть для любого многочлена

Квадратурная формула с узлами, имеющая алгебраический порядок точности, называетсяквадратурной формулой Гауссаиликвадратурной формулой наивысшего алгебраического порядка точности.Очевидно, что квадратурная формула Гаусса является интерполяционной.

Для любого N многочлен степени , удовлетворяющий условию ортогональности (14), имеющий вещественные и различные корни, существует и единственен. Поэтому квадратурная формула Гаусса может быть построена.

Для коэффициентов квадратурной формулы Гаусса верно следующее равенство

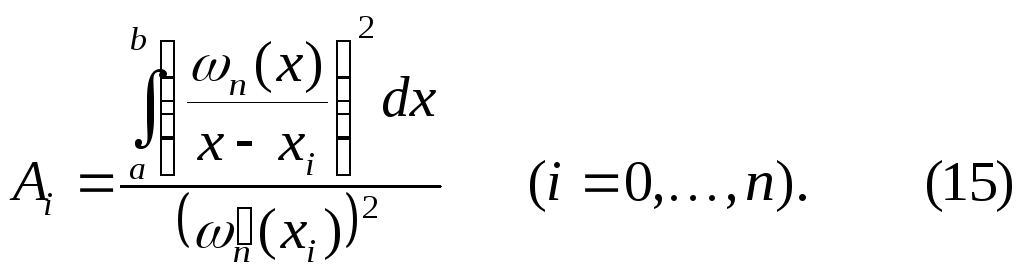
Следовательно, все иОтсюда и из теоремы 2 вытекает сходимость квадратурного процесса, порожденного квадратурной формулой Гаусса.

Квадратурная формула Гаусса дает высокую точность в том случае, когда подинтегральная функция в окрестности отрезка интегрирования обладает высоким порядком гладкости.

Погрешность квадратурной формулы Гаусса для имеет вид

Исторически первым примером квадратурной формулы, имеющей наивысший алгебраический порядок точности, была формула Гаусса для отрезка . Для построения квадратурной формулы использовалась система ортогональных многочленов Лежандра.

Многочлены вида

называются многочленами Лежандра. Из (16) следует, чтоявляется многочленом степени.

Многочлены Лежандра обладают следующими свойствами:

1. Многочлен ортогонален на отрезкелюбому многочленустепени меньше:для любого .

2. Все корни многочлена вещественные, различные и расположены на интервале.

3. Многочлены образуют ортогональную систему на:приипри.

4. Имеет место рекуррентная формула:

Формула (17) позволяет, используя равенства и, найти многочлен Лежандра любой степени.

Если известны корни многочлена Лежандра, то, используя (15), получаем квадратурную формулу Гаусса

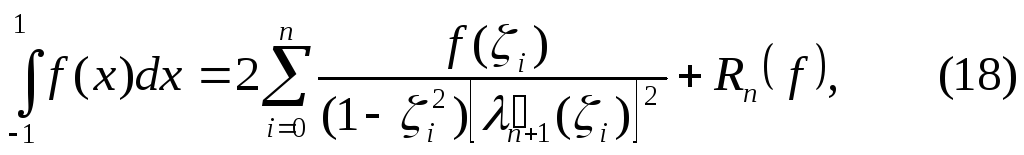
где

Таблицы узлов и коэффициентов формулы (18) приведены в [3]. Отметим, что корнимногочленов Лежандраи коэффициентыквадратурной формулы (18) обладают симметрией наотносительно точки.

Пересчет узлов и коэффициентов квадратурной формулы на произвольный отрезок осуществляется с помощью замены переменной:

Таким образом, из (18) получаем квадратурную формулу Гаусса для произвольного отрезка

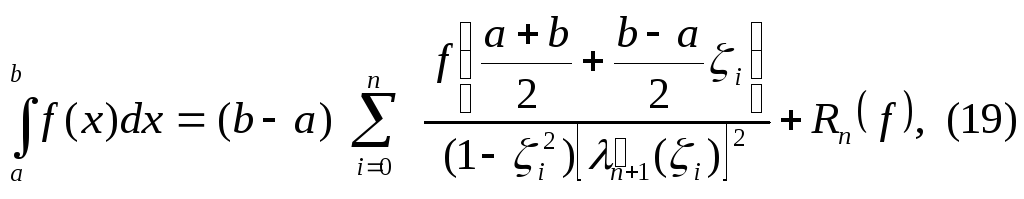
где корни многочлена Лежандра.