
Пространство Rn.
Функции многих переменных:
Множ-во всех упорядоченных наборов х, с координатами х(x1, x2, … xn) из n-веществен. чисел хi€ R для всех n € 1;n назыв. n-мерным арифметическим пространством, обознач. Rn Каждая совокупность х назыв точкой или вектором пространства Rn а число хi-назыв её I координат
Операция сложения и умножения элемента на число вводится как координатное сложение элементов и как умножение каждой координаты на данное число.
Определение Пространство Rn назыв нормированным, если каждому х€ Rn ставится в соответствии неотриц число обозначаемое для всех х€ Rn - ||x|| назыв нормой х и удовлетворяет следующим свойствам
||x||=0↔x=0
||cx||=||c|| ||x|| для всех с€R
||x+y||= ||x||+||y|| для всех х+у€ Rn
Евклидово пространство
![]() - или евклидова
норма.
- или евклидова
норма.
Сходимость последовательности в Rn.
{хn} для всех n€N →xk →xk€Rn
{xk}={x1,x2,…xk..}
{xk}={1/n}={1;1/2;1/3…1/n…}
Если каждому натуральному n€N поставлено в соответствии хк€Rn,то говорят,что задана посл-ть эл-тов в Rn.
Посл-ть хк назыв. Сходящейся к последовательности к эл-ту х0€Rn,если числовая посл-ть стремится к 0.{||xk – x0||}→0,т. Е. если для любого ε>0 сущ kn=k0 (ε)€ N для любого k>k0 : ||xk – x0||<ε.
{xk}→x0 при k→∞ limxk=x0 при k →∞
Замечание.При определении сходимости постед. Не имеет значение способ определения нормы.
Теорема.Сходимость по норме эквивалента по координатной сходимости, т.е. limxk=x0 при k →∞ ↔ limxki=x0 iпри k →∞ для любого i=1;n
Замчание 2. С помощью перехода к координатной сходимости доказыв св-ва сходящ посл-тей: 1)о пределе суммы или разности 2х сход посл-тей; 2)о сходимости произведения сход посл-ти из Rm и сходящейся числовой посл-ти.+
Открытые,замкнутые.компактные мн-ва Rn.
Открытым шаром с центром в точке х0 и рарадиусом δ (иии δ–окрестностью точки х0) назыв мн-ва х€Rn такие,что ||х-х0||<δ= В(х0,δ)
Пусть мн-во Gсодержит Rn точка х0-внутр точка мн-ва G,если она содержится в мн-ве G вместе с некоторым открытым шаром.
Мн-во G назыв открытым,если все его точки внутренние.
Точка х0 назыв предельной точкой мн-ва G,если любая δ-окрестность в этой точке содержит точки мн-ва G, отличные от х0.
[Т] Если х0-предельная точка мн-ва G,то сущ посл-ть хк такая,что хк€G,хк≠х0 и сходится к х0.
Мн-во G замкнуто,если оно содержит все свои предельные точки.
Замечание. Св-ва откр и замкнутых мн-в формулируются аналогично случаю пространства Rn.
Огранич и замкнутое мн-во назыв компактным.
[Т] Если К-компактное мн-во,это эквивалентно тому,что из любой посл-ти {xk} можно выделить сходящ посл-ть,которая сходится к х0€К.
Понятие функции N переменный. Предел функции N переменных.
Ф-ии нескольких(многих) пер-ных,заданных на мн-ве G<Rn, назыв правтло или закон,согласно которому в каждой точке х€Rn ставится в соотвествии единственное число u€R’.
U=f(x)=x вектор=f(x1;x2;…xn)
G-область опр-ния,{u;u=f(x),x€R}-область значения.
По Гейне. Число b называют пределом функции f(M) в точке А (при МА), если для любой последовательности точек {Mn} из множества {M}, сходящейся к точке А (Mn Отлична от А), соответствующая последовательность значений функции {f(Mn)} сходится к b.
По Коши: Число b
называется пределом функии f(M)
в точке А, если для любого числа >0
можно найти такое число >0,
что для всех точек М множества {M}
из
![]() -окрестности
точки А (удовлетворяющих неравенству
р(М,А)<)
выполняется неравенство |f(M)-b|<
-окрестности
точки А (удовлетворяющих неравенству
р(М,А)<)
выполняется неравенство |f(M)-b|<
Замечание. Также,как и в случае одной переменной,доказывается эквивалентность опр-ния предела по Коши и по Гейне,а также св-ва пределов,связанные с арифметич действиями.
[T] Пусть две функции f(M) и g(M) определенные на одном множестве {M}, имеют соответственно пределы b и с в точке А. Тогда функции f(M)g(M), f(M)g(M) и f(M)\g(M) (при с0) имеют пределы в точке А, равные соответственно bc, bc и b\c.
Замечание2.Опр-е не зависит от выбора нормы Rn.
Замечание3. Аналогично случаю ф-ии одной переменной определяется в точке х0 справа и слева и пределы на ∞.
Ф-ия f(x) назыв непрерывной в точке х0€G,если limf(x)=f(x0) при х→х0,т.е.
Функция u=f(M) называется б-м в точке А, если ее предел в ней равен 0
Функция u=f(M) называется б-б в точке А, если ее предел в ней бесконечен
Непрерывность функции N переменных.
Непрерывность функции нескольких переменных
1)Пусть функция u=f(M) определена на множестве {M} н-мерного евклидова пространства. Возьмем точку А{M}, любая -окрестность которой содержит точки множества М.
2)Функция u=f(M) называется непрерывной в точке А, если предел функции в этой точке равен значению функции в этой точке
Следствие: для непрерывных функций знак предела и функции можно поменять местами.
3)Непрерывность функции по Гейне: Функция u=f(M) называется непрерывной в т. А, если для любой последовательности {Mn} сходящейся к А, соответствующая ей последовательность {f(Mn)} сходится к f(A)
4) Функция u=f(M) называется непрерывной в точке K, если для любого >0 найдется отвечающее ему положительное число , такое что для всех M принадлежащих {M}, удовлетворяющих условию р(М,А)< выполняется неравенство |f(М)-f(А)|<
5)Функция u=f(M) непрерывна на множестве {M} если она непрерывна в каждой точке этого множества.
Точки н-мерного евклидово пространства для которых функция u=f(M) не обладает свойством непрерывности называются точками разрыва этой функции.
Приращением или полным приращением функции u=f(M) в точке А называется разность u=f(M)-f(A)
Функция u=f(M) называется непрерывной в точке А, если ее приращение в этой точке является бесконечно малой функцией при M->0.
Непрерывность функции n-переменных по одной из переменных при фиксированных значениях остальных переменных.
Рассмотрим частное приращение функции в точке М (X1,X2,..Xn)
Зафиксируем все переменные этой функции, кроме одной, аргументу X1 дадим приращение x1, имеем:
u=f(x1+x1, x2+x2,…Xn)-f(x1, x2,…Xn)
U=f(x1, x2,…xn)
x1U=f(x1+x1, …xn)-f(x1, x2,…Xn)
Причем x1 М’(x1+x1,…xn){M
Аналогично выводится частное приращение функции по остальным переменным
хnU=f(X1,x2, …, Xn-1, Xn+ xn)-F(x1, x2,…Xn)
Функция u=f(x1,x2,…xn) называется непрерывной в т М(x1, x2, …xn) по переменной Хк, если частное приращение этой функции хкU является б-м функцией при хк->0
Для непрерывных функций справедливые теоремы аналогичные теоремам о непрерывных функциях одной переменной:
функций Пусть функции f(M) и g(M) непрерывны на одном и том же множестве {M}
Тогда функции f(M)g(M), f(M)*g(M) и f(M)\g(M) также непрерывна в точке F
(частное при g(A))
Также справедливы:
теорема об устойчивости знака непрерывной функции
2 теорема Больцано-Коши о прохождении любой непрерывной функции через промежуточ-
ное значение
1 и 2 торемы Вейерштраса.
Частные производные функции N переменных.
Рассмотрим функцию u=f(x1, x2,…xn), заданную на множестве {M}. И пусть точка М(x1, x2, …, xn) внутрення точка области определения множества М
Рассмотрим в данной
фиксированной точке М отношения частного
приращения функции
![]() (Хк0)
Оно должно быть таким, чтобы вновь
полученная т.М с координатами (х1, …Хк-1,
Хк+Хn,Xn+1
….Хn)
принадлежала множеству М.
(Хк0)
Оно должно быть таким, чтобы вновь
полученная т.М с координатами (х1, …Хк-1,
Хк+Хn,Xn+1
….Хn)
принадлежала множеству М.
![]()
Существует
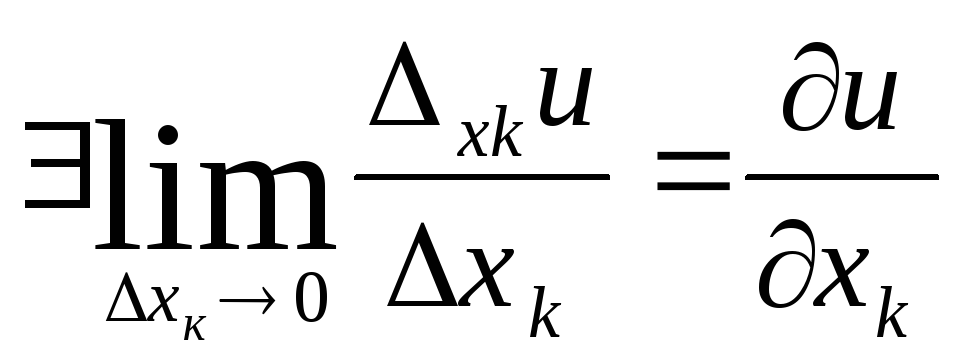 (1)
(1)
D'ef
Если существует предел (1) частных
приращений функции
![]() функцииu=f(x1,
x2,…xn)
в точке М с координатами (х1, х2, ….хn)
по переменной Хк к соответствующему
приращению Хк
аргумента Хк при Хк
-> 0, то этот предел называется частной
производной функции в т.М по аргументу
Хк и обозначается одним из следующих
символов:
функцииu=f(x1,
x2,…xn)
в точке М с координатами (х1, х2, ….хn)
по переменной Хк к соответствующему
приращению Хк
аргумента Хк при Хк
-> 0, то этот предел называется частной
производной функции в т.М по аргументу
Хк и обозначается одним из следующих
символов:
![]() .
.
Замечание. Частная производная представляет собой обычную производную функции. Одной переменной Хк при фиксированных значениях остальных переменных.
Дифференцируемость функции N переменных.
Ф-ия u=f(x) назыв диффер в точке х0,если ее полное приращение в данной точке можно представить в виде ∆u=А1*∆х2+А2*∆х2+…+Аn*∆хn+α(∆х2)*∆х2+…+α(∆хn)*∆хn – ω(х0;∆х),где Аi-некоторые числа,не зависящие от ∆хi.
Перепишем ф-лу: ∆u=A1*∆x1+A2*∆x2+…+An*∆xn+ω(x0;∆x) (2)
|ω(x0;∆x)|/||∆x|| стремится к 0 при ||∆x||→0.
Ф-ия дифференцируема в каждой точке (x1, x2,…,xn),диффер на(x1, x2,…,xn).
[ T]
Если u=f(x1,x2,x3,…,xn)
дифференцируема в точке M(x1,
x2,…,xn),
то существуют частные производные
данной функции по всем переменным,
причем
T]
Если u=f(x1,x2,x3,…,xn)
дифференцируема в точке M(x1,
x2,…,xn),
то существуют частные производные
данной функции по всем переменным,
причем
![]() ,
гдеI=
,
гдеI=![]() .
Доказательство: из условий дифференцируемости
функции запишем:xiU=AiXi+iXi,
I=
.
Доказательство: из условий дифференцируемости
функции запишем:xiU=AiXi+iXi,
I=![]() .
Найдем предел
.
Найдем предел![]() :
:
Следствия:
условие дифференцируемости функции в точке М можно записать в виде: xkU=
 (5)
(5)если u=f(x1,x2,x3…xn) дифференцируема в точке М, то ее представление приращение в форме (2) единственно. Док-во: В ф-ле (2) коэф-ты ∂u/∂xi опр единственным образом(по опр-нию частных произодных).
[Т2] Если u=f(x) диф в точке х0,то она непрер в точке х0. Док-во: lim∆u=0+0=0 при ∆x→0 и ∆хi→0 по опр-нию непрерывности ф-ии,что и т.д.
Замечание. Теорема,обратная теореме 1,не верна.
[Т3] Достаточное условие дифференцируемости функции: Если функция u=f(x1, x2,…,xn) имеет частные производные по всем переменным в некоторой окрестности точки М причем все частные производные непрерывны в самой точке Мо, то указанная функция дифференцируема в этой точке.
Функция u=f(x1,…xn) называется дифференцируемой в т М(x1, x2, …xn), если ее полное приращение представлено в виде
(2)u=A1x1+A2x2+….+AnXn +1x1+…nxn, где А1, А2, …, Аn некоторые числа, не зависящие от X1,X2….X числа, а 1, 2, …m б-м функции соответственно при х1->0, х2->0, …хm->0 Условие называется условием дифференцируемости функции в данной точке М евклидова пространства Еm
Соотношение
(2)называется условием дифференцируемости
функции, причем 1=2….n=0,
при Х1=Х2=Х3…Хn=0
можно записать следующим образом:
![]() u=А1
u=А1![]() Х1+
А2
Х1+
А2![]() Х2)+…+
Аn
Х2)+…+
Аn![]() Хn
Хn
Ф-ия,имеющая в точке х0 непрерывные частные произв-ые,назыв непрерыв диф в точке х0.
Дифференциал функции N переменных.
Дифференциалом du дифференцируемой в точке М(х1,х2,…,хn) функции u=f(x1,x2,…,xn) называется главное линейное относительно приращения аргумента часть приращения этой функции в точке М.
Если все коэффициенты Ai=0, то дифференциал функции в точке М считается равным 0.
Как и в случае 1
перем-ой будем считать,что дифференциал
от независимой переменной совпадает с
ее приращением,т.е. d'xi=![]() i=
i=![]() .du=
.du=![]() (*)
(*)
Замечание1. Ф-ла (*) выписана для случая,когда пргументы хi явл независ переменными.Далее будет доказано,что ф-ла справедлива и в случае,когда хi-зависимые переменные (это св-во назыв инвариантность формы первого диффер-ла).
Замечание2. Геометр смысл диф-ла 2х переменных. (рис.)
Дифференцирование сложной функции.
Рассмотрим вопрос о дифференцировании сложной функции нескольких переменных вида:
U=f(M)=f(X1,x2,…xn) (1)
Xi=i(t1,t2,…,tk), I=1,2,…m (2)
[T]
Пусть функция (2) дифференцируема в
некоторой точке Nо
(![]() ,
а функция (1) дифференцируема в точке
Мо(
,
а функция (1) дифференцируема в точке
Мо(![]() ,
причем
,
причем![]() Тогда сложная функцияu=f(x1,x2,…,xn),
где Х1,Х2,…,Хn
определяется по формулам (2) дифференцируема
в точке Мо, при этом частные производные
этой сложной функции вычисляются по
формулам:
Тогда сложная функцияu=f(x1,x2,…,xn),
где Х1,Х2,…,Хn
определяется по формулам (2) дифференцируема
в точке Мо, при этом частные производные
этой сложной функции вычисляются по
формулам:
![]()
….
![]()
в которых
![]() берутся в точкеMо,
а частные производные
берутся в точкеMо,
а частные производные
![]() берутся
в точкеNо.
берутся
в точкеNо.
Следствие:
Случай,когда ф-ла (2) зависит только от
t1
хi=φi(t),поэтому
ф-ла примет вид
![]()
Неявные функции.
D'ef Если переменная u, являющаяся по смыслу функцией переменных х1,х2,…,хn задается посредством функций уравнений F(U,X1,x2,…,xn)=0, то говорят, что функция задана неявно.
Частные производные неявно заданной функции вычисляются по формулам:
d'u/d'xi=-(d'F/d'xi)/(d'F/d'u), i=1,...,n
Рассмотрим совокупность М неявных функций, которые задаются посредством системы М функциональных уравнений:
/u1=ф1(х1,х2,...,хn)
/u2=ф2(х1,х2,...,хn) (1)
\...
\um=фm(х1,х2,...,хn)
Пусть функции определены, как решение М функциональных уравнений (2)
(2)
/F1(u1,...,um,x1,...xn)=0
/F1(u1,...,um,x1,...xn)=0 (2)
\...
\F1(u1,...,um,x1,...xn)=0
Решением системы (2) будет называться совокупность функций, таких что при их подстановки в систему все уравнения этой системы образуются в тождества.
D'ef Это решение будем называть непрерывным и дифференцируемом в некоторой области D' изменения переменных Х1,Х2,…Хn Если каждая из функций U1,U2,…Um непрерывна и дифференцируема в этой области.
ld'F1/d'u1, d'F1/d'u2,..., d'F1/d'un l
ld'F2/d'u1, d'F2/d'u2,..., d'F2/d'un l = D'(F1,F2,...,Fn)\D'(u1,u2,...,un)
l... l
ld'Fm/d'u1, d'Fm/d'u2,..., d'Fm/d'unl
Такой определитель называют определителем Якоби или Якобианом.
[T] Система (2) будет разрешима, а решение непрерывно и дифференцируемо, если функция f1,f2,…,fn дифференцируема в окрестности точки Мо, d'Fi/d'ui непрерывна в точке Мо, D'(F1,F2,...,Fn)\D'(u1,u2,...,un)
Якобиан отличен от 0 и F1=F2=…=Fn в точке Мо
Производная по направлению. Градиент.

Рассмотрим функцию
трех переменных u=f(x,y,z).
Пусть она определена в некоторой
окрестности точки Мо(хо,yo,zo).
Рассмотрим всевозможные лучи, выходящие
из точки Мо. Каждый такой луч заадется
единственным вектором (соs,
cos,cos).
Если l-
длина этого отрезка, то его координаты
![]() (lcos,
lcos,
lcos)
C
другой стороны:
(lcos,
lcos,
lcos)
C
другой стороны:
![]() (x-xo,
y-yo,
z-zo)
(x-xo,
y-yo,
z-zo)
Т.о. получили один и тот же отрезок:
Приравняем

u=f(Xo+lcos, Yo+lcos, Zo+lcos) (1)
Т.о. u- сложная функция.
Производную
указанной сложной функции по переменной
l,
взятую в точке l=0
нназывают производной функции u=f(x,y,z)
в точке Мо по направлению, оопределяемому
единичным вектором l.
Обозначение:
![]()
(2)
Градиентом функции
u=f(x,y,z)
в данной точке Мо(xo,yo,zo)
называется вектор, координаты которого
имеют вид gradu(Mo)=![]()
Если: u=f(x1,x2,…,xn)
Mo(![]()
[Т] Вектор градиента функции y=f(x,y,z) в точке Мо характеризует направление и величину максимального роста функции в точке Мо,т.е. производные функции u=f(x,y,z) в точке Мо по направлению, определенному вектором градиента этой функции в точке Мо имеет максимальное значение по сравнению с производной по любому другому направлению и это значение равно длине вектора градиента.
Док-во: Из ф-л (1) и(2) →(gradu,e) =∂u/∂e
∂u/∂e=(gradu,e) = |gradu|*|e|*cosφ
Cosφ=1 φ=0
Max значение достигается ↔ вектор е и вектор grad направлены одинаково. Тогда |∂u/∂e=gradu|
Следствие. Вектор градиента не зависит от выбора координат.
Геометрический смысл градиента:
Линии уровня для функции двух переменных u=f(x,y) называется линия на которой функция сохраняет свое постоянное значение.
Если В каждой точке линии уровня M(xо,yо) построить касательную, то вектор-градиент в точке Мо будет перпендикулярен этой касательной.
Поверхность уровня- фунция u=f(x,y,z) в точке Мо (xo,yo,zo) называется поверхность на которой функция сохраняет свое постоянное значение.
Свойства: если в каждой точке Mo(xo,yo,zo) провести касательную поверхность, то вектор градиент будет ортогонален этой поверхности.
Частные производные высших порядков функции N переменных.
Пусть u=f(x) диф в окрестной точке х0,значит в окр точке сущ. частные производные Пусть частные производные сущ. в каждой точке области D ∂u/∂xi=di=1,n, если она сущ в каждой обл D то её можно рассматривать как некоторую функцию нескольких переменных, заданных на обл D следовательно у неё существуеют частные производные d'u/d'xi, i=1,...,n: d'/d'xk(d'u/d'xi)=d^2u/(d'xid'xk)
Частная производная взятая от d'u/d'xi, i=1,...,n по переменной Хк называется частной производной второго порядка и обозначается d'^2u/d'xid'xk, i=1,...,n шне равно к, если I=k, то она обозначается как d'^2u/d'xi^2
Смешанные частные производные второго порядка для непрерывной функции равны. Аналогично, равные смешанные частные производные 3, 4 и т.д.
Теорема.Пусть ф-я диф к-раз в точке х0,то в этой точке значение любой смешанной частной производной к-го порядка(последовательности), где происходят последовательное диф, т.е. ∂2u/∂xi∂xj =∂2u/∂xi∂xj
Локальный экстремум. Необходимые условия.
Пусть функция u = f (х) f(x1^0,x2^0,...,хn^0)
Определение. Функция u= f(x) определена в окрестной точке х0 имеет в точке локальный максимум (минимум), если существует такая окрестность точки xo, такая что в её пределах значение f(x) явл наиб(наим) среди всех значений этой функции.
Определение ф-я u=f(x) имеет в точке ч0 локальный экстремум если она имеет в этой точке либо лок макс, либо лок мин
Теорема (необходимое условие)
Если функция u = f(x1,x2,...,xn) имеет в точке хo (х1^0, x2^0,...,xn^0) локальный экстремум и частные производные первого порядка, то все эти частные производные равны нулю в точке Mo: d''u/d''xilMo=0, i=1,2,…,n.(!)
Доказательство. Зафиксируем все значения переменных xi, кроме переменной хk положив их равными x1^0. Тогда получим, что функция u = f(x1^0, х2^0, ...,x(k-1)^0,xk,x(k+1)^0,...,x(n)^0) зависит от одной переменной хk и в точке хk = хk^0 имеет локальный экстремум. Но тогда производная этой функции, которая и является частной производной d''u/d''xк в точке Mo,равна нулю, что и требовалось доказать. а
Заметим, что необходимые условия локального экстремума (!) определяют, что в точке локального экстремума d''ulMo=0.(*). Обратное утверждение также верно: если в точке Мo первый дифференциал функции тождественно равен нулю (как функция относительно ), то все частные производные этой функции в указанной точке равны нулю в силу произвольности d''xi.
Замечание Данное условие явл.необходимым,но не достаточным
Определение.Точки которорые обращаются в ноль все частные производные первого порядка,назыв стационарными точками или точками возможного экстремума ,он может существовать,а может не сущ его наличие можно установить только достаточным условием
Следствие.Если u=f(x) имеет в точке х0 диф и имеет лок экстр то диф в точке х0 тождественно равен 0 относительно диф dxj
Достаточные условия локального экстремума функции N переменных.
Пусть функция u=f(M) один раз дифференцируема в некоторой окрестности точки Мо и два раза дифференцируема в самой точке Мо, пусть кроме того Мо – стационарная точка. Тогда:
Если d''^2u в точке Мо положительно определенная квадратичная форма относительно переменных d''x1,d''x2,…,d''xn, то Мо – точка локального минимума
Если d'^2u в точке Мо отрицательно определенная квадратичная форма, то Мо – точка локального Максимума.
Если d'^2u в точке Мо знакопеременная квадратичная форма, то экстремум в точке Мо не существует.
Частный случай:
[Т] пусть функция u=f(x,y) один раз дифференцируема в окрестности точки Мо с координатами (хо,уо) и два раза дифференцируема в самой точке Мо и пусть Мо – стационарная точка, тогда если в точке Мо выполнено условие:
, (d'^2u/d'x^2*(M0))* (d'^2u/d'y^2*(M0))-(d'^2u/d'xd'y)^2>0 то функция имеет в точке Мо локальный экстремум, причем если d'^2u/d'x^2в точке Мо>0 , то Мо точка локального минимума.
Если d'^2u/d'x^2 (Мо)<0 то Мо точка локального Max
Если же (d'^2u/d'x^2*(M0))* (d'^2u/d'y^2*(M0))-(d'^2u/d'xd'y)^2<0 то экстремум в точке Мо не существует.
Квадратичная форма. Критерий Сильвестра.
Рассмотрим функцию специального вида. Квадратичная форма:
Функция Ф(t1,t2,…,tk)= E(i=1,k)E(k=1,n)aiktitk называется квадратичной формой, где Аik коэффициенты квадратичной формы, t1,t2,…,tn- переменные квадратичные формы, d''^2u квадратичная форма относительно d''x1, ….,d''xn c коэффициентом Aik=.d''^2/ud''xid''xk Если Aik=Aki, то квадратичная форма называется симметричной. Данной квадратичной форме ставится в соответствие матрица коэффициентов квадратичной формы.
Матрицей А размера mXn называется прямоугольная таблица чисел содержащая m строк и n столбцов.
Матрица называется квадратной, если число строк равно числу столбцов.
Симметричной: Aik=Aki
Определителем матрицы называется число характеризующее матрицу d'etA
Существуют способы вычисления d'et:
Минор- некоторый фрагмент матрицы.
Главными минормаи матрицы А называются следующие определители:
А1=А1.1
А2=а1.1*А2.2-А2.1*А1.2
А3=А1.1*А2.2*А3.3+А2.1*А2.2*А1.3+А3.1.*А2.2*А1.3-А3.2.А2.3А1.1-А2.1А12А33
Аm=d'etA
Квадратичная форма называется положительно определенной, если для любых значений t1,t2,…,tn одновременно не равных 0 она принимает строго положительные значения.
Квадратичная форма называется отрицательно определенной если для любых значений неравенств t1,t2,…tn она принимает строго отрицательные значения.
Квадратичная форма называется знакопеременной если она принимает как строго положительные, так и строго отрицательные значения при разлиынх наборах t1,t2,…tn
Критерий Сильвестра знакопеременной квадратичной формы:
Для того, чтобы квадратичная форма или матрица была положительно определнной необходимо и достаточно, чтобы все главные миноры матрицы А были положительными.
Для того чтобы квадратичная форма или мтарица была отрицательно определнной необходимо и достаточно, чтобы знаки главных миноров чередовались, причем первый был отрицательный.
Замечание: если хоть одно из условий не выполняется, то форма знакопеременная
Теорема о разрешимости системы функциональных уравнений.
Дано:система функциональных уравнении т.е. пусть m-ф-ции
/y1=g1(x1,x2,…,xn)
(1) <y2=g2(x1,x2,…xn)
\ym=gm(x1,x2,…xn)
ищутся как решение системы m функциональных уравнении.
/F1(y1,y2…ym,x1,x2,…xn)=0
(2) <F2(y1,y2,…ym,x1,x2,…,xn)=0
\Fm(y1,y2…ym,x1,x2,…xn)=0
(1):yi=gi(x1,x2,…xn),i=1;n
(2):Fi=(u1,u2,…um,x1,x2,…xn)=0, i=1;m
Определение:Решение системы(2) называется совокупностью m ф-ции системы(1) таких,что при их подстановки в систему(2) все уравнения системы(2) обращаются верными тождествами.Это решение называется непрерывным и дифференцируемым на некотором открытом множестве Д изменение переменных х1.х2.,,,хт,если каждая из функции системы (1)непрерывна и дифференцируема на Д
(gradF1 )
F= (gradF2 ) (3)-матрица Якоби для ф-ции Fi по переменной ui и обозначает Д(F1,F2,…Fm) /( Д(u1,u2,…um)
( gradF3 )
Определитель матрицы F называется якобианом
Теорема: пусть m ф-ции стоящеи в левои части системы (2) в некоторой окрестности точки М0ЄЕ причем частные производные этих ф-ции Fi по переменным ui непрерывны в точке М0.Пусть все эти ф-ции Fi обращаются в точке М0 в 0 ,а якобиан D(F1,…Fm)/D(u1,…um)≠0 тогда для любых ε>0 существует окрестность в точке М’0ЄЕ' в пределах которой существуют единственные М ф-ции gi системы(1) такие что они удовлетворяют условию | gi-gi° |<εi i=1,m и является решением системы (2) причем это решение непрерывно и дифференцируемо в этои окрестности точки М'0
Замечание:При m=1 эта теорема становится теоремой о дифференциале неявных ф-ции.
Условный экстремум
Задача отыскания экстремума функции аргументы которой удовлетворяют дополнительному условию связи называется задачей отыскания условного экстремума.
Рассмотрим вопрос отыскания экстремума функции z=f(u1,u2,…um,x1,x2,…,xn)
Будем говорить, что эта функция при наличии условий связи
/F1(u1,...um,x1...,xn)=0
/F2(u1,...um,x1...,xn)=0
\...
\Fm(u1,...um,x1...,xn)=0
(2)имеет условный максимум (минимум) в точке Мо, координаты которой удовлетворяют этим условиям связи, если существует окрестность точки Мо, для которой значение этой функции в точке Мо является наибольшим (наименьшим) среди всех точек координаты которых удовлетворяют эти условиям связи.
Первый способ решения задачи условного экстремума:
Основная его идея – переход от задачи условного экстремума к задаче безусловного экстремума.
Пусть у функции F1, F2, …Fm дифференцируема в окрестности точки Mо и непрерывны в окрестности точки Мо. Пусть, кроме того, ЯкобианD'(F1,F2,...Fn)/D'(u1...,un) неравен 0 в точке Мо. Тогда система (2) имеет непрерывное дифференцируемое решение
/u1=ф1(x1,x2,xn)
/u2=ф2(x1,x2,xn)
\...
\un=фn(x1,x2,xn)
Подставим это решение в функцию 2: z= f(ф1(х1,х2,...,хn), ф2(х1,х2,...,хn)... фn(х1,х2,...,хn)
Метод множителей Лагранжа.
Метод неопределенных множителей Лагранжа. Если система функций уравнений (2) неразрешима, либо ее решение затруднительно для вас, используют более универсальный способ – метод неопределенных множителей Лагранжа. Идея та же – переход от условного экстремума к безусловному.
L=f+л1F1+л2F2+…+лmFm (4)
Функция Лагранжа.
Теперь находим экстремум этой функции. Здесь л1, л2,…лn –множители Лагранжа.
Предположим, что функция дифференцируема
L(u1,u2,…um,x1,x2,…,xn,1,2,…n)
Необходимые условия экстремума:
/d'L/d'u1=0...
/d'L/d'um=0
/d'L/d'x1=0... необходимые условия экстремума
\d'L/d'xn=0
\F1=0
\Fn=0
Эта система содержит u+2m уравнений и u+2m переменных.
Мо( u10,...,um0,x10,...,xn0)
о( k10,...,лm0)
![]()
Для полученных точек проверяем достаточное условие экстремума.
Достаточное условие экстремума
Пусть ф. u-f(x1…..xn) один раз дифференцируема в некоторой окрестн. (.) M0 и 2 раза дифференцируема в самой (.)M0. пусть кроме того M0-стационарная (.) Тогда если d2u положительно определённая квадратичн. форма от переменных dx1…..dxn, то ф. имеет в (.)M0 локальный минимум
Если d2u отриц. определённая квадратичн. форма, то ф. имеет в (.)M0 локальный максимум
Если d2u знакопеременная квадратичная форма, то M0 не явл. (.) экстремума
Замечание: при проверке критерия знакоопределённости квадратичной формы d2u мы анализируем матрицу А
d2u/dx12 d2u/dx2dx1 ….. d2u/dx1dxn
А= d2u/dx2dx1 d2u/dx22 ….. d2u/dx2dxn
…………………………………………
d2u/dxndx1 …………………. d2u/dxn2
Теор. Пусть ф. u=f(x,y) 1 раз дифференцруема в окрестности (.) M0(x0,y0) и 2 раза в самой (.) M0 , тогда если в (.) M0 выполняется условие d2u/dx2 * d2u/dy2 - d2u/dxdy * d2u/dydx >0, то экстрем. В (.) M0 существует , причём если d2u/dx2 > 0, то M0 (.) минимума; если
d2u/dx2 < 0 , то M0 (.) максимума
Если d2u/dx2 * d2u/dy2 - d2u/dxdy * d2u/dydx <0, то экстрем. ф. в (.)M0 не существует.
Понятие первообразной. Основные свойства (лемма, теорема)
ФункцияF(x)
называется первообразной для функции
f(x)на
некотором промежутке Х, если для любого
х
![]() Х выполняется условиеF’(x)=f(x).
Например, функция F(x)=sinx
является первообразной для функции
f(x)=cosx
на всей прямой, т.к. при любом значении
x(sinx)’=cosx
Х выполняется условиеF’(x)=f(x).
Например, функция F(x)=sinx
является первообразной для функции
f(x)=cosx
на всей прямой, т.к. при любом значении
x(sinx)’=cosx
Замечание.Задача нахождения первообразной решается неоднозначно.Действительно,если F(х) первообразная,то F(х)+с,где с-const,также явл первообразной,т.к. (F(х)+с)′=F′(х)+0=f(х) для всех х€Х.
Лемма: Функция, производная которой на некотором промежутке Х равна 0 постоянна на этом промежутке. f’(x)=0(xX), то f(x)=c для всех х€Х.
Доказательство:Рассмотрим
2точки
![]() .Пусть
х1<х2,тогда по Т. Лагранжа,f(x2)-f(x1)=f’(х0)(x2-x1),
где х0€ (x1;x2).
Т.к. f’(х0)=0,
то f(x2)=f(x1)=0,
т.е. f(x)=С,
где С- некоторое число.
.Пусть
х1<х2,тогда по Т. Лагранжа,f(x2)-f(x1)=f’(х0)(x2-x1),
где х0€ (x1;x2).
Т.к. f’(х0)=0,
то f(x2)=f(x1)=0,
т.е. f(x)=С,
где С- некоторое число.
[Т] Если F(x)- первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x)+C.
Доказательство: Пусть F(x)- первообразная для функции f(x) на некотором промежутке Х, т.е. F’(x)=f(x). Пусть Ф(х) некоторая другая первообразная для функции f(x) на промежутке Х, т.е. Ф’(x)=f(x). Тогда для любого хХ (Ф(x)-F(x))’=Ф’(x)-F’(x)=f(x)-f(x)=0 Т.о. мы получили, что производная функции равна 0, а это означает по лемме, что функция Ф(х)-F(x) постоянна, т.е. Ф(х)-F(x)=С, на промежутке Х, где С- некоторое число. Следовательно, Ф(х)=F(x)+C.
Следствие 1: множество функций F(x)+C исчерпывает все множество первообразных функций для f(x).
23. Услоловия сущ-ия опр интеграла.Суммы Дарбу.Необход и достат условия.
[Т](необход усл) Если ф-ия f(x) интегрир на отрезке [a,b],то она непрерывна на этом отрезке.
Замечание. Данное усл-е не явл достаточным.
Ф-я Дарбу [a,b]
F(x)= 0,x-иррац
1,х-рац
[0,1]-разбиением τ1 в качестве точек αi1 – иррац.
Разбиением τ2 αi2 - рац.
σ= ∑f(αi1)∆01=0
σ= ∑f(αi2)∆20=|b-a|=1 при i=1
Т.о. посл-ть интеграл сумм не имеет предела при λ→0.
Замечание. Сущ. Необходимые и достат усл-я,которые устанавливаются при помощи понятия суммы Дарбу.
Понятие неопределенного интеграла.
Если функция F(x) является первообразной для функции f(x) на промежутке Х, то множество функций {F(x)+C} называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается символом f(x)dx=F(x)+C. При этом f(x) называется подынтегральной функцией, f(x)dx- подынтегральным выражением, а переменная х- переменная интегрирования. f(x)dx- выражает множество всех первообразных для функции f(x) на промежутке Х.
Восстановление функции по ее производной,т.е. отыскание неопределенного интеграла называется интегрированием этой функции, т.к. F’(x)=f(x) F’(x)dx=F(x)+C
Интегрирование- операция обратная дифференцированию.
Замечание1.Чтобы проверить правильное интегрирование достаточно продифференцировать результат и получить при этом подынтегральную функцию.
Замечание2.Далее будет доказано,что любая непрер функция имеет на этом отрезке первообразную,сл-но неопр интеграл.
Таблица основных интегралов:
0dx=C
dx=x+C
х dx=
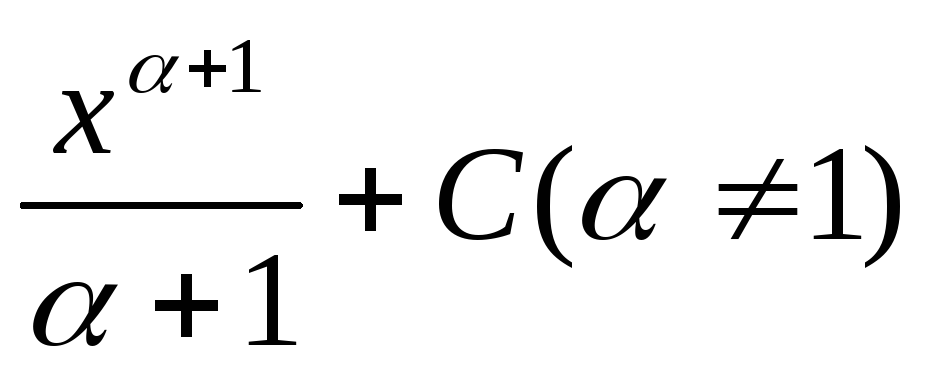
ахdx=ах/lna+C
dx/x=ln|x|+C
eхdx=eх+C
sinxdx=-cosx+C
cosxd'x=sinx+C
dx/cos2x=tgx+C
dx/sin2x=-ctgx+C
dx/
 =arcsinx +C=-arccosx+c
=arcsinx +C=-arccosx+cdx/1+x2=arctgx+C=-arcctgx+C
dx/x2+ a2 =1/a arctgx/a+C
dx/x2-a2 =1/2a ln|x-a/x+a|+C
dx/
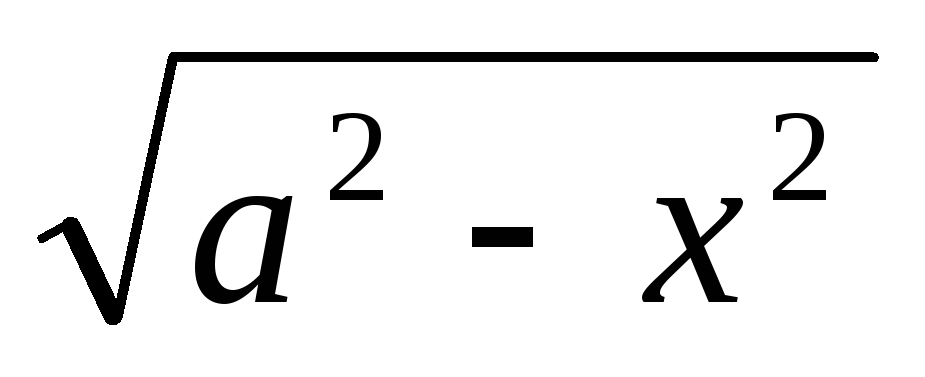 =arcsin x/a +C
=arcsin x/a +Cdx/
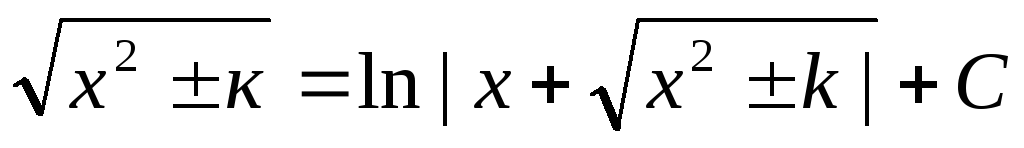
Основные свойства неопр интеграла:
(f(x)dx)’=f(x) и d'( f(x)dx)=f(x)dx Доказательство: (f(x)dx)’=(F(x)+C)’=F’(x)=f(x) и df(x)dx=(f(x)dx)’dx=f(x)dx
dF(x)=F(x)+C. Доказательство: т.к. d'F(x)=F’(x)d'x, то по определению F'(x)d'x=F(x)+C
kf(x)dx=kf(x)dx. Доказательство: (kF(x))’=kF’(x)=kf(x). Из определения следует, что kf(x)dx=k[F(x)+C]=kF(x)+C1=kf(x)dx, где С1=кС, ч.т.д.
(f(x)g(x))dx=f(x)dxg(x)dx. Доказательство: пусть F(x) и G(x) являются первообразными для функций f(x) и g(x) на промежутке Х, т.е. хХ F’(x)=f(x), G'(x)=g(x). Тогда функции F(x)G(x) являются первообразными для функция f(x)g(x). Следовательно, f(x)dxg(x)dx=(F(x)+C1)(G(x)+C2)=(F(x)G(x))+(C1C2)=[F(x)G(x)]+C=(f(x)g(x))dx
Основные методы интегрирования.Рекурентные формулы.
Непосредственное интегрирование.
Это вычисление интеграла с помощью непосредственного исп-ия таблиц простейших интегралов и основных св-в неопред интегралов.
Метод подстановки или метод замены переменных.
Достаточно часто введение новой переменой позволяет свести интеграл к табличному
[Т] Пусть функция х=(t) определена и дифференцируема на некотором промежутке Т и пусть Х- множество значений этой функции, на котором определена функция y=f(x), т.е. на T определена сложная функция y=f[(t)]. Тогда если на множестве Х функция f(x) имеет первообразную F(x), то справедлива формула f(x)d'x|x=(t)= f[(t)]’(t)d't. Доказательство: Пусть функция F(x) является первообразной для функции f(x). Рассмотрим на множестве T сложную функцию F[(t)]. Продифференцируем ее по правилам дифференцирования сложной функции: F’[(t)]*’(t)=f’[(t)]*’(t)
мы получили что эта функция имеет на множестве Т первообразную F[(t)]. f[(t)]*’(t)d't=F[(t)]+C=F(x)+C|x=(t)= f(x)d'x|x=(t). Получили искомую формулу.
Метод интегрирования по частям.
Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций.
[Т] Пусть функции u(x) и v(x) определены и дифференцируемы на некотором промежутке Х и пусть функция u’(x)*v(x) имеет первообразную на этом промежутке, т.е. существует v(x)u’(x)d'x. Тогда на промежутке Х функция имеет u(x)v’(x) также имеет первообразную и справедлива формула: u(x)v’(x)d'x=u(x)v(x)- v(x)u’(x)d'x. Доказательство: Из равенства [u(x)*v(x)]’=u’(x)v(x)+u(x)v’(x) следует u(x)v’(x)=[u(x)v(x)]’-u’(x)v(x). Первообразной функции [u(x)v(x)]’ на промежутке Х является функция u(x)v(x). Функция u’(x)v(x) имеет первообразную на Х по условию теоремы. Следовательно, и функция u(x)v’(x) имеет первообразную на промежутке Х (как разность интегрируемых функций). Интегрируя последнее равенство, получим формулу u(x)v’(x)d'x=u(x)v(x)- v(x)u’(x)d'x (формула интегрирования по частям в неопределенном интеграле).
Т.к. v’(x)d'x=d'v, u’(x)d'x=d'u, то ее можно записать в виде ud'v=uv-vd'u.
За u выбирают ту часть подынтегральной функции, которая упрощается дифференцированием, а за d'v ту часть, интеграл от которой существует
Основные типы интегралов берущихся по частям.
Общие рекомендации: Практика показывает, что большая часть интегралов берущихся по частям может быть выделена в следующие группы:
Подынтегральная функция содержит в виде множителя одну из следующих функций: arctgx, arcctgx, arcsinx, arccosx, степени этих функций, а также lnx- их полагают за u, а оставшаяся часть это производные известных функций, т.е. интеграл от оставшейся части подынтегрального выражения существует.
Интегралы вида (ax+b)n sinkx, (ax+b)n coskx, (ax+b)n екх, где а,b,к=const, n- натуральное число. Эти интегралы берутся n- кратным интегрированием по частям. U=(ax+b)n 1kn, d'v- оставшаяся часть выражения.
Интегралы вида: ехasin(bx)d'x, еaxcos(bx)d'x, sin(lnx)d'x, cos(lnx)d'x. Исходный интеграл обозначается за I, берется 2 раза по частям и получаем в правой части выражение, содержащее исходный интеграл I, т.е. мы получаем уравнение относительно исходного интеграла, решаем его относительно I.
Рекуррентная формула
Ik=89…….Ik-1
Рекуррентная формула доказывается с помощью интегрирования по частям
Ik=1/2a2(k-1)
(t/(t2a2)k+(2k-3)![]() dt/(t2a2)k-1
)
(K>2)
dt/(t2a2)k-1
)
(K>2)
Сущ. интегралы, берущиеся по частям и не относящиеся ни к какой из вышеперечисленных групп.
Интегрирование рациональных функций
Важным классом функций, интегралы от которых всегда выражаются через элементарные функции,образуют класс рациональных функций,т.е. функций кот. Моно представить в виде Р(х)/Q(х), где Р,Q-многочлены в некоторой степени х
Р(х)=аnxn+an-1xn-1+…+a2x2+a1x+a0-общий вид
Р(х)=ах2+bx+c=a2x2+a1x+a0
P(х)=ax+c= a1x+a0
Если степень многочлена в числители равна и больше степени многочлена в знаменателе, то выполнить деление можно,выделив верхнюю часть P(x)/Q(x)=V(x)+R(x)/Q(x) Степень R(x)<Q(x), a V(x)-многочлен некоторой степени.
[Т1] Каждый многочлен может быть представлен в виде Q(x)=A(x-a1)1 (x-a2)2….. (x-ak)k Или Q(x)=(x2+p1x+q1)1 (x2+p2x+q2)2……… (x2+plx+ql)l (*)
А-коэффициент при старшей степени х
[Т2-о разложении
рац функции на элементар множители]
Если рациональная функция
![]() имеет степень многочлена числителяn
меньше, чем степень многочлена знаменателя
m
и многочлен Q(x)
имеет вид (*), то эту функцию можно
единственным образом представить в
виде:
имеет степень многочлена числителяn
меньше, чем степень многочлена знаменателя
m
и многочлен Q(x)
имеет вид (*), то эту функцию можно
единственным образом представить в
виде:
![]() =
=![]()
![]()
![]()
![]()
![]() …
…![]() …
…![]()
![]() …
…![]() …+
…+![]()
![]() …
…![]() (**)
(**)
Метод неопределенных коэффициентов.
Метод неопределенных коэффициентов
Он заключается в том, чтобы следовать алгоритму: Записать представление 1, привести правую часть к общему знаменателю и группировать при степенях Х, получим дроби с равными знаменателями, присваиваем числители. Получим 2 многочлена, они равны если равны коэффициенты при соответствующих степенях Я, следовательно составляем систему уравнений, приравнивая коэффициенты при соответствующих степенях Х.
Вычисление интегралов 1-4типов.
Основные типы интегралов, берущихся по частям.
А/х-а dx= Ad(x-a)/x-a=Aln|x-a|+C
Аdx/(х-а)k=A (х-а)-kd(x-a)=A(x-a)1-k/1-k+C (k1)
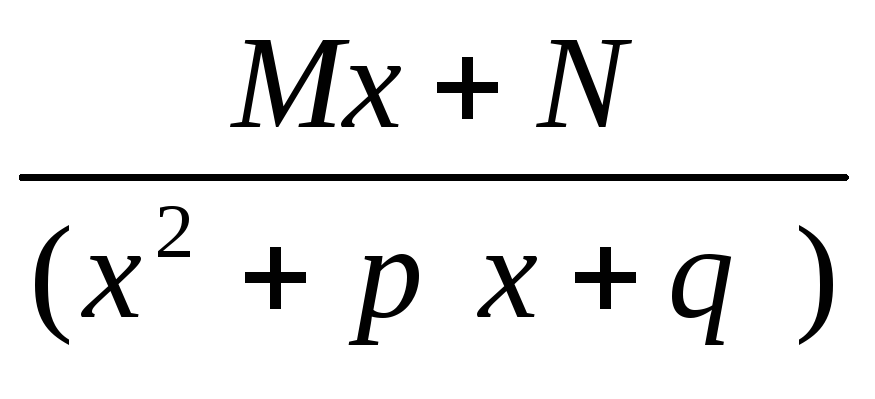 dx=M/2
dx=M/2 +N
+N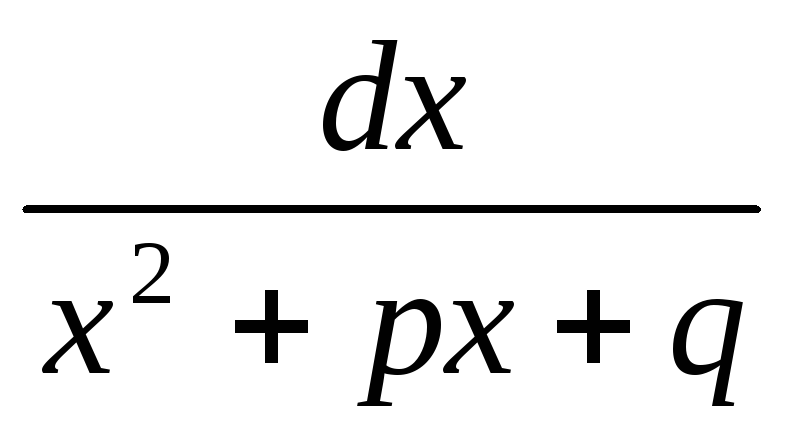 =M/22x+p/x2+px+q
dx +(N-MP/2)dx/
x2+px+q=M/2ln|
x2+px+q|+(N-MP/2)dt/t2+a2
=M/22x+p/x2+px+q
dx +(N-MP/2)dx/
x2+px+q=M/2ln|
x2+px+q|+(N-MP/2)dt/t2+a2
x2+px+q=(
x2+2p/2x+p2/4)+q-p2/4=(x+p/2)2+(q-p/4)=т.е.
![]() dx=M/2(x2+px+q)-kd(x2+px+q)+(N-Mp/2)
dx=M/2(x2+px+q)-kd(x2+px+q)+(N-Mp/2)
dt/(t2a2)k=M/2(x2+px+q)1-k/1-k +(N-MP/2)Ik
Интегрирование иррац. и трансцендентных функций.
Предварительно введем обозначение рац. Функции от двух переменных u v, т.е. функции получающиеся из двух переменных u v и некоторых постоянных, над которыми производятся только операции сложения, вычитания, умножения и деления
Интеграл вида ,где a,b,c,d числа R рац. Функция от х и от Такой интеграл рационализируется подстановкой t=
Интеграл вида ,где a,b,c,d некоторые числа а не рвно 0 R рац. Функция от х и от
Интеграл вида SR(sin, cos)dx, где Rрац функция от SIN и от COS. Интеграл рационализируется подстановкой t=tgx/2
Интеграл вида SR(ex)dt рац подстановкой t=eх.
Понятие определенного интеграла.
Пусть λ=max∆I – длина наиб. Частичнго отрезка λ→0.
Если существует
конечный предел I
интегральных сумм
при 0,
то этот предел называется определенным
интегралом Римана для функции f(x)
по отрезку [a,b]
и обозначается I=![]() =
=![]() (**)
(**)
D'ef
функция f(x)
называется интегрируемой на [a,b]
если для любой последовательности
разбиений {Xk},
у которой
![]() соответствующая
последовательность интегральных сумм
{k}
стремится к одному и тому же числу I.
соответствующая
последовательность интегральных сумм
{k}
стремится к одному и тому же числу I.
D'ef
Число I
называется определенным интегралом по
Риману для функции f(x)
оп отрезку [a,b],
если для любого >0
сущесвтует такое >0,
что при
(т.е. если отрезок [a,b]
разбит на части с длинами Xi<)
независимо от выбора точек I
выполняется неравенство
![]() ,
или же
,
или же![]()
Замечание.Число I
называется определенным интегралом
Римана от функции f(x)
по сегменту [a,b]
и обозначается так: I=![]() ,
где а- нижний предел,b-
верхний предел
,
где а- нижний предел,b-
верхний предел
Следует отметить,
что
![]() =
=![]() =
=![]()
Услоловия сущ-ия опр интеграла.Суммы Дарбу.Необход и достат условия.
Основные свойства определенного интеграла.
1.
 =0
=0
Если а>b,
то по определению
![]() =
-
=
-![]() (4),
т.е. когда отрезок [a,b]
при a<b
пробегает в направлении от b
к а, имеем b=X0,
а=Xn,
Xi=Xi-Xi-1<0
(4),
т.е. когда отрезок [a,b]
при a<b
пробегает в направлении от b
к а, имеем b=X0,
а=Xn,
Xi=Xi-Xi-1<0
2.
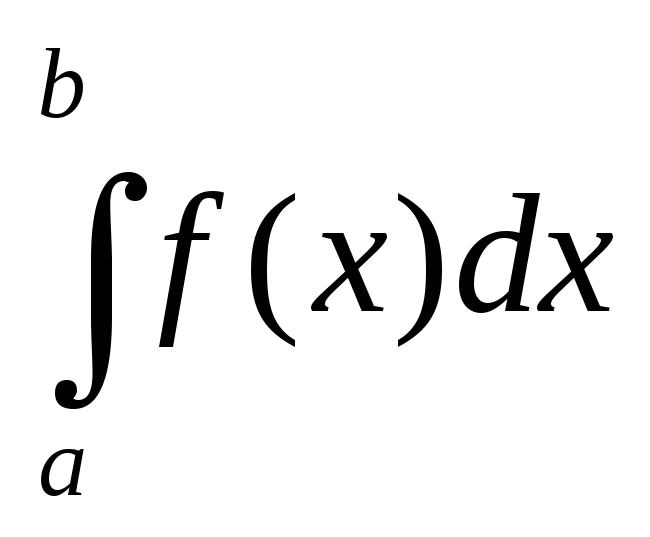 =
=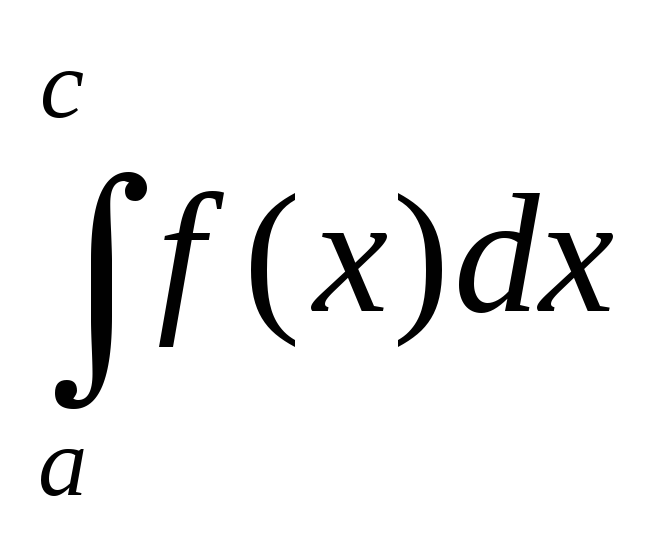 +
+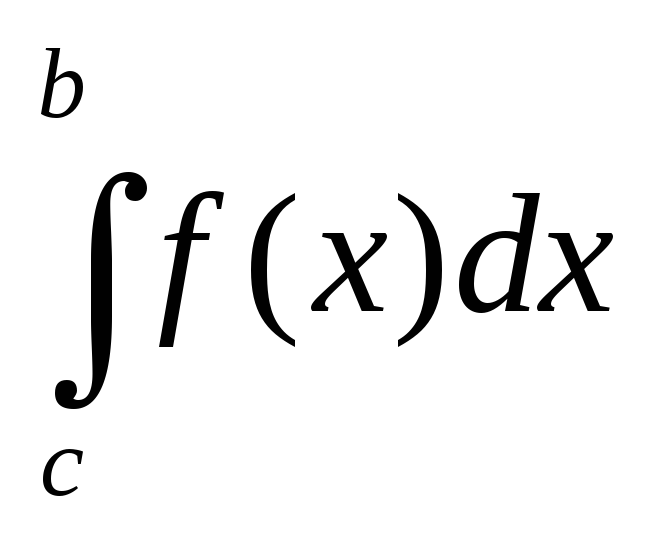 (здесь и в дальнейшем предполагается,
что интегралы, входящие в доказываемые
формулы существуют)
(здесь и в дальнейшем предполагается,
что интегралы, входящие в доказываемые
формулы существуют)
Доказательство:
Допустим сначала, что а<c<b,
т.к. предел интегральной суммы
не зависит от способа разбиения отрезка
[a,b],
то будем проводить разбиение так, чтобы
точка с всегда была бы точкой разбиения
[a,b].
Если например с=хm,
то
можно разбить на две суммы: =![]() =
=![]() +
+![]() .
Переходя в последнем равенстве к пределу
при
мы и получим искомое равенство.
.
Переходя в последнем равенстве к пределу
при
мы и получим искомое равенство.
Суть доказанного свойства состоит в том, что определенный интеграл по всему отрезку равен сумме интегралов по его частям.
Доказательство
для другого расположения точек a,
b, c легко сводится к рассмотренному
случаю. Пусть, например, а<b<c,
тогда по доказанному, имеем:
![]() =
=![]() +
+![]() ,
откуда учитывая (4) получаем
,
откуда учитывая (4) получаем![]() =
=![]() -
-![]() =
=![]() +
+![]() ,
ч.т.д.
,
ч.т.д.
Постоянный множитель можно выносить за знак определенного интеграла, т.е.
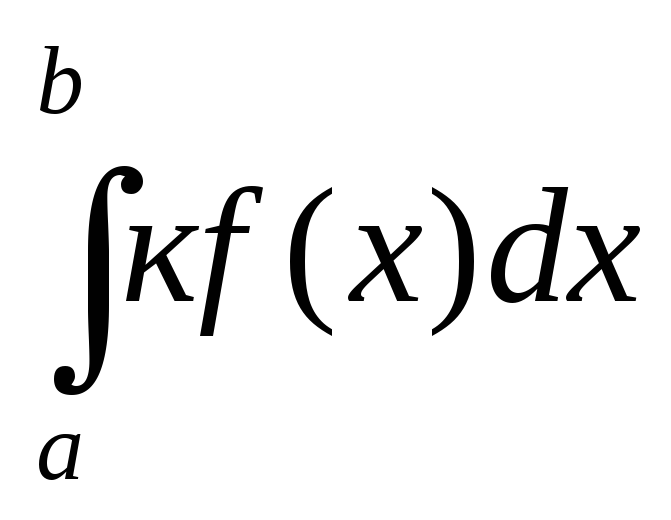 =к
=к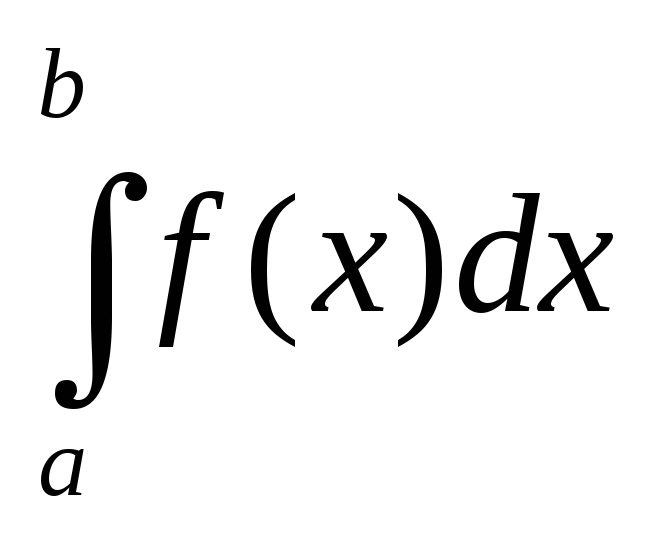 .
Доказательство: действительно, для
любого разбиения отрезка [a,b]
и любого выбора точек I
.
Доказательство: действительно, для
любого разбиения отрезка [a,b]
и любого выбора точек I
 =k
=k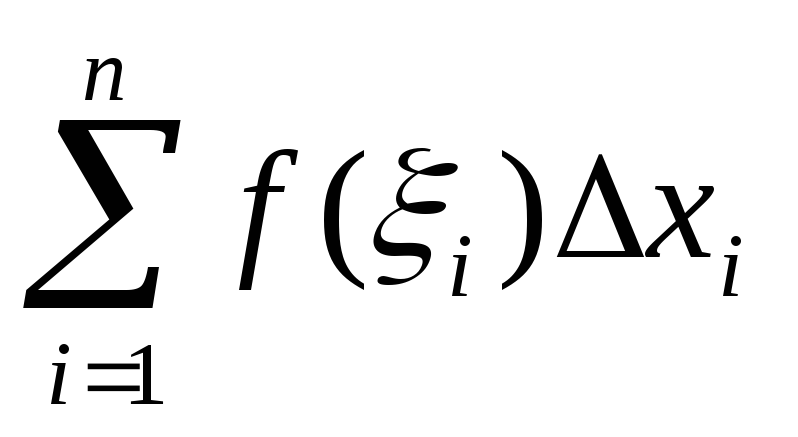
Переходя к пределу
при 0
имеем
![]() =
=![]() =
=![]() =к
=к![]() =
к
=
к![]() .,
ч.т.д.
.,
ч.т.д.
Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т.е.

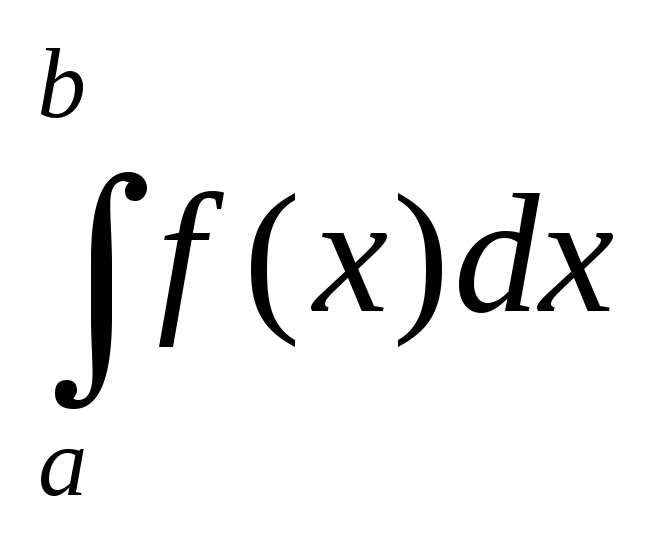
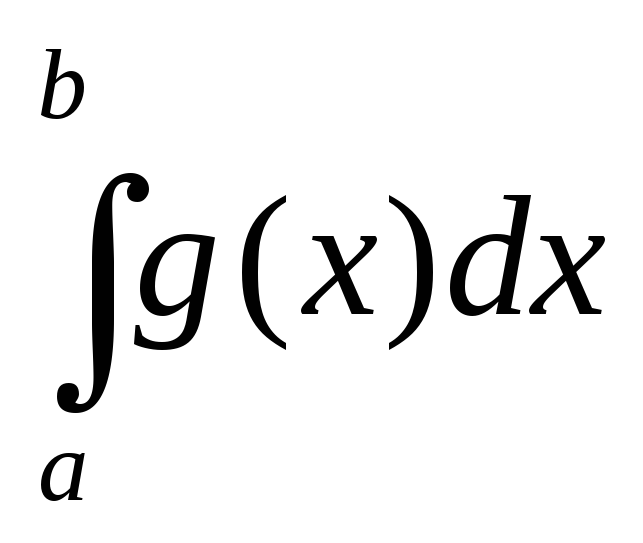 .
Доказательство: действительно, для
любого разбиения отрезка [a.b]
и любого выбора точек I
.
Доказательство: действительно, для
любого разбиения отрезка [a.b]
и любого выбора точек I
 =
=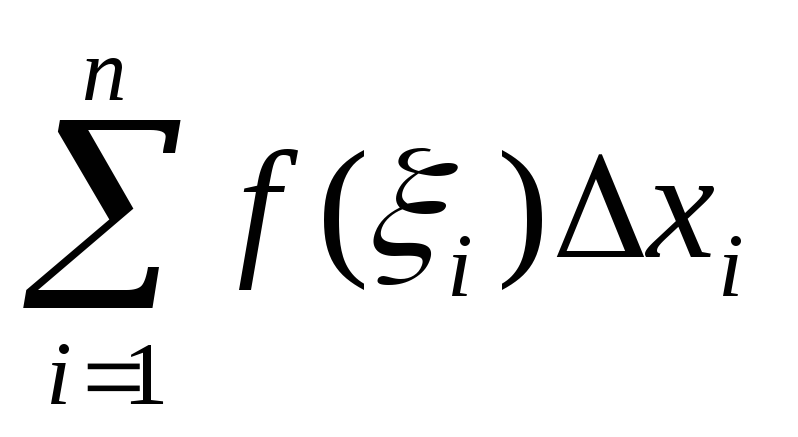
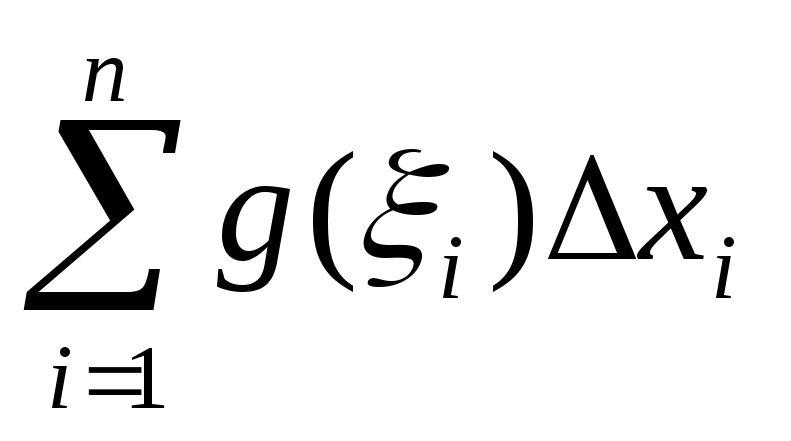 Так
как
Так
как
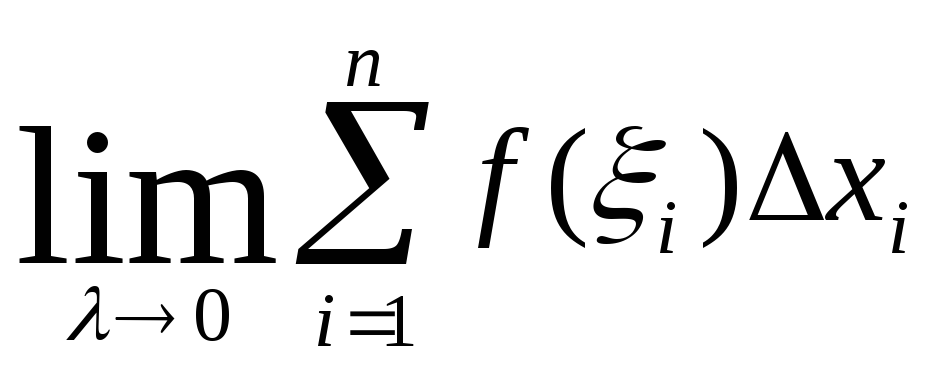 =
=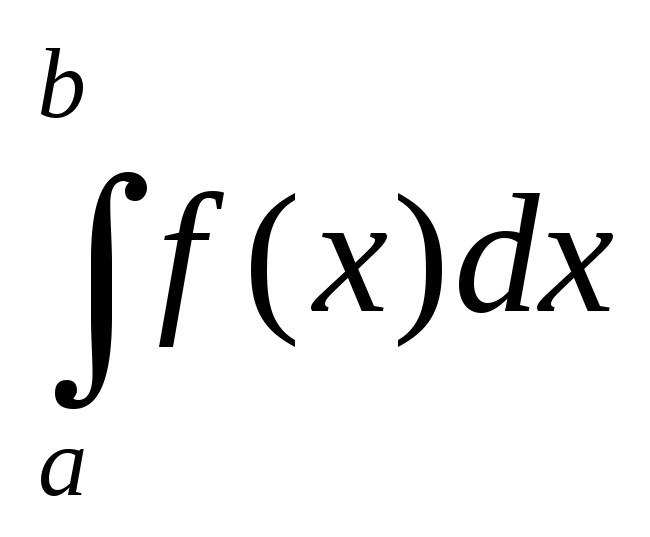 и
и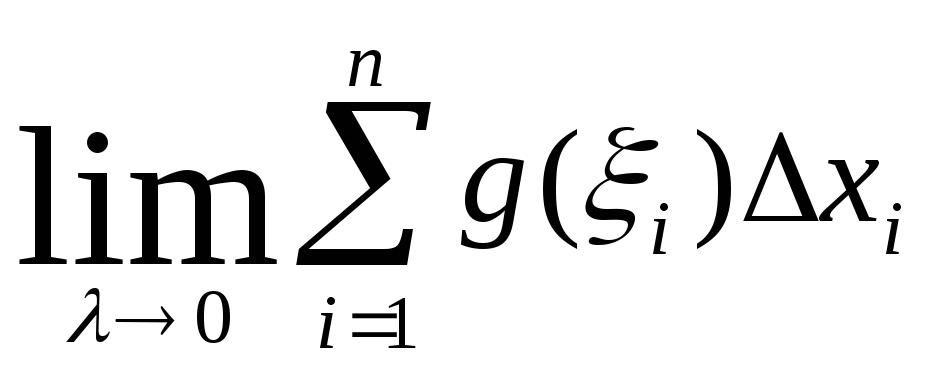 =
=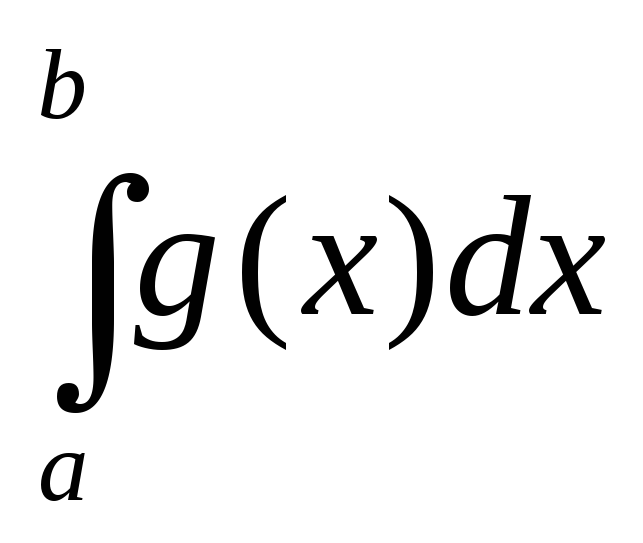 ,
то получаем что
,
то получаем что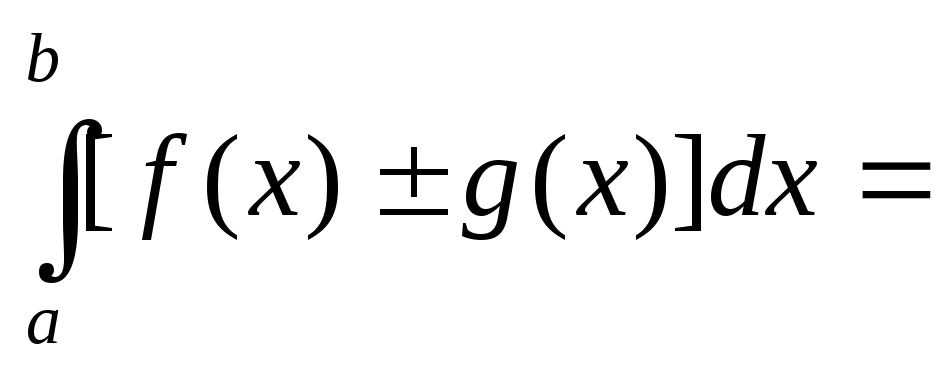

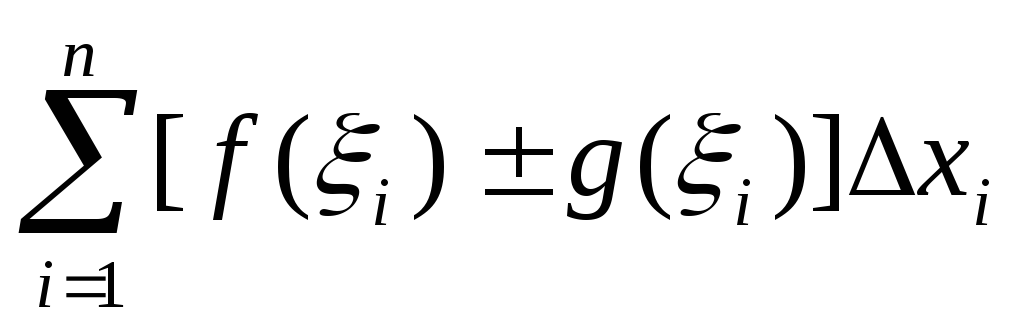 =
=
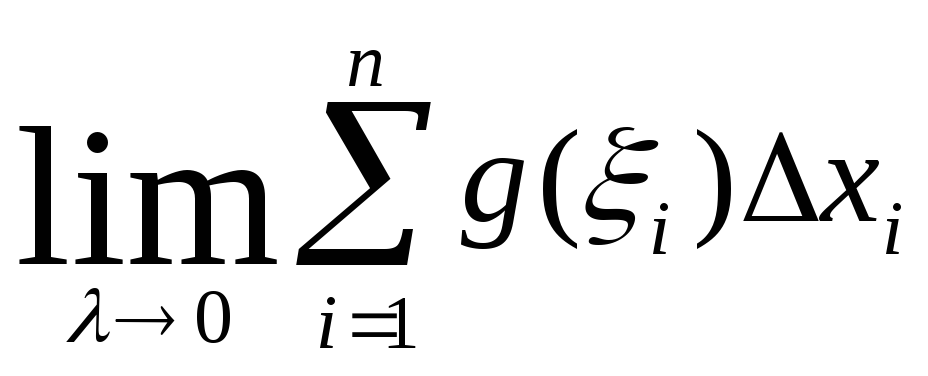 =
=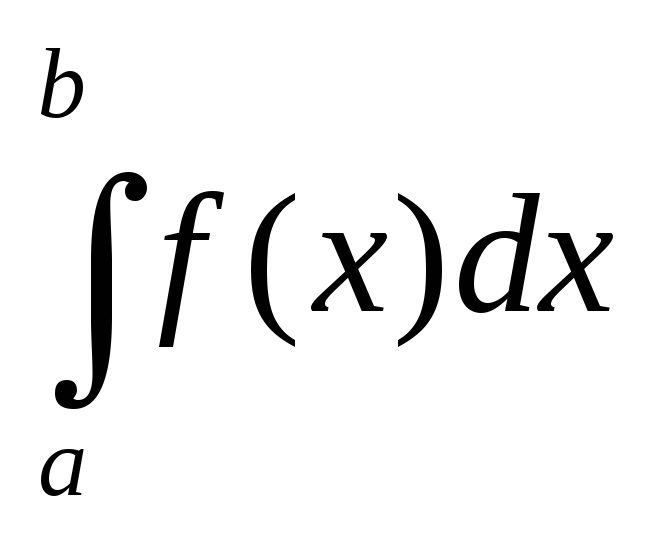

Оценки интегралов. Формула среднего значения.
[Т] Если функция
f(x)
непрерывна на сегменте [a,b]
то существует т С, принадлежащая этому
сегменту, такая что
![]() =f(c)(b-a).
Эта формула называется формулой среднего
значения.
=f(c)(b-a).
Эта формула называется формулой среднего
значения.
Замечание: теорема о среднем имеет четкий геометрический смысл: величина определенного интеграла при f(x)>=0 равна площади прямоугольника имеющего высоту f(c) и основание b-a.
[Т] Пусть а<в.
Если f(x)≥0 для любого х€[a,b]→∫от а до в f(x)≥0
Если f(x) ≥g(x) для любого х€[a,b]→∫f(x)dx≥∫g(x)dx
Если f(x) опред на [a,b]→|∫f(x)dx|≤∫f(x)dx
Если |f(x)|≤k для любого х€[a,b]→|∫f(x)dx|≤k*(b-a)
Пусть m,M соответств наим и наиб значения ф-ии f(x) на [a,b],тогда справедлива ф-ла m(b-a)=∫f(x)dx≤M(b-a)
Интеграл с переменным верхним пределом.
Интеграл с переменным верхним пределом.
![]() x
[a,b]
x
[a,b]
Это интеграл у которого нижний предел а=const а верхний предел х переменный. Величина этого интеграла представляет собой функцию верхнего предела х
(х)=
![]() ,
где х принадлежит сегменту [a,b]
и ф(х)= интеграл с переменным верхним
пределом. Геометрически интеграл с
переменным верхним пределом представляет
собой S
криволинейной трапеции.
,
где х принадлежит сегменту [a,b]
и ф(х)= интеграл с переменным верхним
пределом. Геометрически интеграл с
переменным верхним пределом представляет
собой S
криволинейной трапеции.
[Т] Производная
интеграла от непрерывной функции по
переменному верхнему пределу существует
и равна значению подынтегральной функции
в точке, равной верхнему пределу, т.е.
Ф’(x)=(![]() )’x=f(x)
)’x=f(x)
Ф’(x)=(
![]() )’=f(x)
)’=f(x)
Ф’(x)=![]()
Замечание. Т.о., любая непрер на отрезке функция f(х) имеет на этом отрезке первообр, которой явл интергал с перемен верхним пределом Ф(х),т.к. любая др первообр может отлич на константу,то сущ связь между опр и неопр интегралом.
Формула Ньютона-Лейбница.
Пусть Ф’(х)=f(x) и F’(х)=f(х) - др первообр.
Ф(х)=F(x)+C,![]() =F(x)+C,
где С- некоторое число, axb.
Подставляя в это равенство значение
х=а и используя свойство 1, имеем:
=F(x)+C,
где С- некоторое число, axb.
Подставляя в это равенство значение
х=а и используя свойство 1, имеем:
![]() =0,
получим: 0=
=0,
получим: 0=![]() ,F(a)+C,
C=-F(a)
,F(a)+C,
C=-F(a)
Т.е. для любого
х[a,b]
![]() Полагая
здесь х=b
получим искомую формулу.
Полагая
здесь х=b
получим искомую формулу.
Замечание 1.В качестве F(х) можно взять любую первообр для f(х) на отрезке [a,b].
Замечание 2. Ф-ла Ньютона-Лейбница явл методом вычисления опр интеграла.
Замена переменных в определенном интеграле.
[T] пусть функция f(x) непрерывна на [a,b] и пусть выполнены следующие условия:
функцию х=(t) дифференцируема на [,] и ’(t) непрерывна на [,]
Множеством значений функции х=(t) является отрезок [a,b]
()=a и ()=b, то справедлива формула

Доказательство: По формуле Ньютона- Лейбница:
Пусть F(x)- первообразная для функции f(x) на [a,b].
Рассмотрим сложную
функцию Ф(t)=F((t))
Согласно правилу дифференцирования
сложной функции находим:
Ф’(t)=F’((t))*’(t)=f((t))’(t).
Отсюда следует, что функция Ф(t)
является первообразной для функции
f((t))’(t),
непрерывной на [,]
и поэтому согласно формуле Ньютона-Лейбница
получаем,
![]() =
Ф()-Ф()=F(())-F(())=F(b)-F(a)=
=
Ф()-Ф()=F(())-F(())=F(b)-F(a)=
![]()
Замечание1. При исп-нии данной ф-лы не надо возвращ от новой переем-ной t к старой х.
Замечание 2. При исп-нии ф-лы надо проверять соблюдение всех условий.
Формула интегрирования по частям в определенном интеграле.
[T]
Если функция u(x)
и v(x)
имеют непрерывные производные на [a,b]
то справедлива формула
![]()
Доказательство
Так как функция u(x)
и v(x)
по условию имеют производные, то по
правилу дифференцирования произведения
[u(x)v(x)]’=u(x)v’(x)+v(x)u’(x).
Откуда следует, что функция u(x)v(x)
является первообразной для функции
u(x)v’(x)+v(x)u’(x).
Тогда по формуле Ньютона-Лейбница
![]() Отсюда
Отсюда![]() ,
ч т.д.
,
ч т.д.
Приложение определенного интеграла: площадь криволин трапеции,длина дуги плоской кривой,объем тела вращения и площадь поверхности.
Рассмотрим плоскую
фигуру, ограниченную [a,b]
оси Ох, прямыми x=a,
x=b
и графиком непрерывной и неотрицательной
функции y=f(x)
на [a,b].
S=![]()
Геометрический смысл определнного интеграла: определенный интеграл от неотрицательной непрерывной функции f(x) на [a,b] численно равен площади криволинейной трапеции.
Несобственные интегралы с бесконечными пределами.
Пусть функция f(x)
определена на промежутке [a;
+)
и интегрируема на любом отрезке [a,R],
R>0,
так что интеграл
![]() имеет смысл, Предел этого интеграла приR
называется несобственным интегралом
первого рода и обозначается
имеет смысл, Предел этого интеграла приR
называется несобственным интегралом
первого рода и обозначается
![]() (1). В случае, если этот предел конечен,
говорят, что несобственный интеграл
сходится, а функциюf(x)
называют интегрируемой на бесконечном
промежутке [a,
+),
если же предел бесконечен или не
существует, то говорят, что несобственный
интеграл расходится.
(1). В случае, если этот предел конечен,
говорят, что несобственный интеграл
сходится, а функциюf(x)
называют интегрируемой на бесконечном
промежутке [a,
+),
если же предел бесконечен или не
существует, то говорят, что несобственный
интеграл расходится.
Аналогично вводится
понятие несобственного интеграла по
промежутку (-,
b].
![]() .
Наконец, несобственный интеграл с двумя
бесконечными пределами можно определить
как сумму несобственных интегралов
.
Наконец, несобственный интеграл с двумя
бесконечными пределами можно определить
как сумму несобственных интегралов![]() ,
где с- любое число.
,
где с- любое число.
Геометрический смысл несобственного интеграла первого рода состоит в том,что несобств интеграл первого рода-это площадь соотв заштрих бесконечной области.
Несобственные интегралы от неограниченных функций.
Определение1.Пусть f(x), определенную на отрезке(a,b],иограниченна на на любом отрезке [a+,b], 0< <b-a,. В таком случае х=а называется особой точкой.
Определение2. Пусть
функция f(x)
определена на промежутке (a,b],
если особой является точка х=а, и сущ.
конечный предел то несобственных
интеграл второго рода определяется как
![]() При
этом говорят, что несобственный интеграл
сходится, если же предел не сущ или равен
бесконечности, то говорят что несобствен.
интеграл расходится
При
этом говорят, что несобственный интеграл
сходится, если же предел не сущ или равен
бесконечности, то говорят что несобствен.
интеграл расходится
Определение3.Точка х=в явл. особой точкой для f(х), если f(x) неогран. В любой окрестности данной точки, но огран на любом отрезке [а.b-] для всех >0 таких что a<b-<b
Определение4. Пусть
х=в особая точка для f(x)
определенной на[a,b)
тогда если сущ конечный предел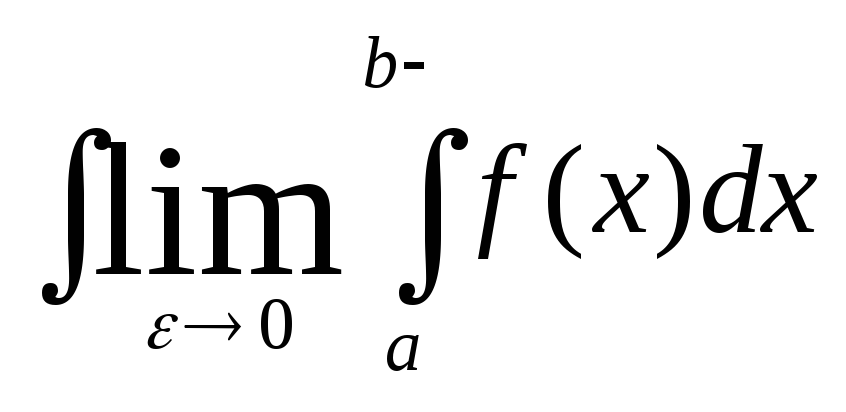 то
он называется несобствен интегралом
второго родап и обознач.
то
он называется несобствен интегралом
второго родап и обознач.![]()
Определение5. Если
а и b
особые точки, т.е. функция С ограничена
и интегрируема на интервале (a,b),
то несобственный интеграл второго рода
определяется в виде суммы
![]() ,
где с- произвольная точка на (a,b),
а несобственные интегралы второго рода
в правой части этого равенства определяются
соответственно по формулам.
,
где с- произвольная точка на (a,b),
а несобственные интегралы второго рода
в правой части этого равенства определяются
соответственно по формулам.
Определение6. f(x) определена на отрезке (a,b) за искл. точки d которая назыв особой опред. Как сумма двух несобственных интегралов.При условии что оба интграла сущ.
Признаки сходимости несобственных интегралов.Примеры.
Теорема (признак сравнения несобственных интегралов). Пусть функции f(x) и g(x) непрерывны на промежутке [a , ∞) и удовлетворяют на нём условию 0 ≤ f(x) ≤ g(x). Тогда из сходимости интеграла a ∫ ∞g(x) dx (1) следует сходимость интеграла a∫∞f(x)dx (2) и наоборот, из расходимости интеграла(2) следует расходимость интеграла (1).Доказательство: Введём обозначения F(R)=a∫Rf(x)dx, G(R)=a∫Rg(x)dx, причём 0≤F(R)≤G(R).
Функции F(R) и G(R) являются неубывающими; в самом деле, если a≤R1≤R2, то R1∫R2f(x)dx≥0 и тогда F(R2)=a∫R2 f(x)dx=a∫R1f(x)dx+R1∫R2f(x)dx≥a∫R1f(x)dx=F(R1).
Возьмём последовательность значений {Rn}→∞; тогда соответствующая последлвательность значений функции {F(Rn)} является монотонной и неубывающей. Пусть интеграл (1) сходится, тогда последовательность {G(Rn)} ограничена, но тогда ограничена и последовательность {F(Rn)}, а значит в силу теоремы(монотонная ограниченная последовательность сходится)она сходится. Следоавтельно, существует предел F(R) при R→∞, т.е. интеграл (2) сходится.
Теперь докажем вторую часть теоремы: пусть интеграл(2) расходится. Если предположить, что интеграл (1) сходится, то по доказанному выше интеграл(2) также должен сходится, что противоречит условию. Теорема доказана.
ЗАМЕЧАНИЕ. Аналогичный признак сравнения справедлив и для несобственных интегралов второго рода. Если функция f(x) и g(x) непрерывны на полуинтервале [a,b) и для всех точек в окресности особо точки b выполняются условия0≤f(x)≤ g(x), то из сходимости интеграла a∫b g(x)dx следует сходимость интеграла a∫b f(x)dx, а из сходимости интеграла a∫bf(x)dx следует расходимость интеграла a∫bg(x)dx.
ТЕОРЕМА (критерий Коши). Для сходимости несобственного интеграла(2) необходимо и достаточно, чтобы для любого ε>0 можно было найти такое A>0, что для любых R' и R'', больших, чем A, выполняется неравенство |F(R'')-F(R')=|R’∫R’’ f(x)dx|<ε
Определние и услвия сущ-ния двойных интегралов.Геом смысл.Св-ва.
Пусть G – замкнутая (содержит все свои точки) и ограниченная область.
Ф-я z=f(x,y) на этой области определена и ограничена.
Граница области G составлена из точек yi=fi(x) и xi=fi(y).
Введем понятие интегральной суммы:
1. Разобьем обл. G на n произвольных частей (Gi, i=1,n). Gi – частичная область. Полученные частичные области не имеют общих точек. Si, i=1,n – площадь частичной области.
В каждой частичной области выберем точку с координатами (αI,βI). Вычислим значение ф-и в этой точке (f(αI,βI)) и составим такую сумму:
n
(1) =f(αI,βI)Si
i=1
(1) – интегральная сумма ф-и f(x,y) в обл G.
dI – диаметр области Gi
- диаметр разбиения: =maxdI
Определение
Если интегральная сумма (1) при 0 имеет предел, равный I, то этот предел называется от ф-и f(x,y) по области G и обозначается:
I=f(x,y)dxdy
G
f(x,y) – подынтегральная функция.
Если , то говорят, что ф-я f(x,y) интегрируема по области G, G называют областью интегрирования; х,у – переменными интегрирования; dxdy– элементом площади.
Замечание. Условие огранич ф-ии z=f(x,y) явл необходим,но не достаточным.
Достат условие формулировки с исп-ем сумм Дарбу (кот полностью переносится аналогично в ф-лу).
Теорема1. Ф-ия f(x,y) непрерывная в замкнутой огран обл G,интегрир в обл G.
Теорема2. Ф-ия f(x,y) огран в замкнутой огран обл G и непрер в ней всюду,кроме точек …….. на конечном числе кривых явл графиками ф-ии y=f(x) и x=g(y),где f и g непрер и интегрир в этой обл.
Геометрический смысл
Пусть в пространстве дано тело Р, ограниченное:
1.Сверху – графиком непрерывной и неотрицательной функции z=f(x,y)
2.Снизу – областью G
3.Сбоку – цилиндрической поверхностью.
Направляющей этой цилиндрической поверхности является область G, а образующими – прямые, || оси z.
Такое тело называется криволинейным цилиндром
Интегр сумма σ-это сумма объемов цилиндриков,в которой можно принять приближенно за тело Р,это приближенное равенство тем точнее,чем меньше область разбиения G на части,т е при переходе к пределу при 0 мы получаем равенство
n
VP = limf(α,β)Si.
0 i=1
Т.о. геометрический смысл :
от непрерывной, неотрицательной, ограниченной функции равен объему криволинейного цилиндра.
Следствие: Если f(x,y) 1 для всех (x,y)€G,то I=f(x,y)dxdy =lim при λ→0 ∑f(α,β)* Si= limSi = SG.
0 i=1
Свойства .
1.kf(x,y)d'xd'y = kf(x,y)d'xd'y
2. (f(x,y) + g(x,y))d'xd'y = f(x,y)d'xd'y + Gg(x,y)d'xd'y.
3. f(x,y)d'xd'y = f(x,y)d'xd'y + f(x,y)d'xd'y.
Теорема о среднем:
Если ф-я f(x,y) непрерывна в области G, то в этой области точка с координатами (αI,βI), такая, что
f(αI,βI)*S = f(x,y)d'xd'y, где S – площадь области G.
Сведение двойного интеграла к повторному(2случая).
1сл. Теорема о переходе от к повторному для прямоугольной области.
Рассмотрим по некоторому прямоугольнику D' со сторонами, параллельными осям координат.
Теорема: Пусть для ф-и f(x,y) в прямоугольной области D'={(x,y)|axb; cyd'}
f(x,y)d'xd'y.(1)
D'
Пусть, кроме того, для каждого х из отрезка [а;b] определенный интеграл
d'
I(x)=f(x,y)d'y.(2)
c b b d'
Тогда интеграл I(x)d'x = d'xf(x,y)d'y, называемый
a a c
повторным, и справедливо равенство:
b d'
f(x,y)d'xd'y = d'xf(x,y)d'y.(3)
D' a c
Замечание: Если в теореме х и у поменять ролями, то будет доказано существование повторного интеграла
d' d' b
I(y)d'y = d'yf(x,y)d'x
c c a
и справедлива формула
d' b
f(x,y)d'xd'y = d'yf(x,y)d'x. (8)
D' c a
С помощью формул (3) и (8) двойной интеграл приводится к повторному.
Пример.
