2. Применение мультипольных разложений

Рассмотрим особенности мультипольных разложений в тех случаях, когда распределение заряда обладает определенной симметрией. Отдельно изложим применение сферических и декартовых СК.

1. Сферически-симметричное распределение заряда.

В этом случае объем, занимаемый зарядами, имеет сферическую форму и плотность распределения зарядов зависит только от расстояния от начала координат: .

1. Применение ССК

Пусть - радиус поверхности, ограничивающей распределение зарядов. Мультипольные моменты согласно равны

Учитывая и , находим

Где - полный заряд. На расстояниях , в области его применимости, мультипольное разложение сводится к одному единственному вкладу

2. Применение ДСК

Компоненты тензора мультипольного момента -го порядка имеют структуру (см. ):

Поскольку выделенные направления в задаче отсутствуют, тензор должен конструироваться только из компонентов изотропного тензора , где - символ Кронекера. Отсюда сразу заключаем, что все нечетные мультипольные моменты равны нулю:

Этот вывод также следует из свойств симметрии подынтегрального выражения в .

Четные моменты отличны от нуля. Для их построения необходимо воспользоваться свойствами перестановочной симметрии

между любой парой индексов и , что следует непосредственно из . Таким путем мы находим:

Для определения достаточно левую и правую части умножить на и свернуть по обоим индексам:

Так как

то из уравнения следует:

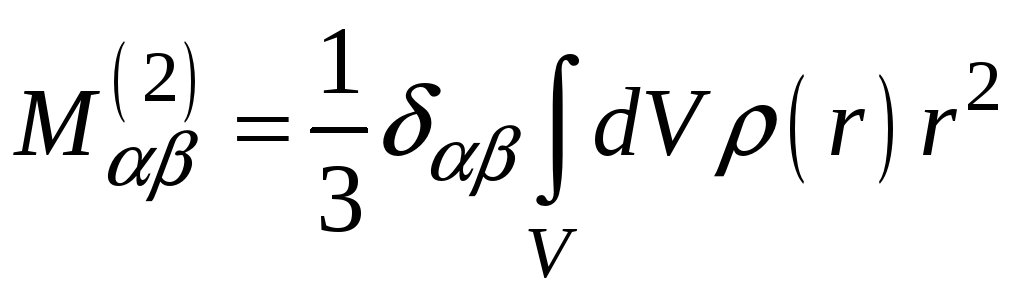
Постоянная определяется аналогично: умножением левой и правой части на комбинацию

и сверткой по всем парам индексов. Это приводит к

и т.п.

Рассмотрим теперь свертку тензоров . В компонентах,

Подставляя сюда выражение , находим:

Нетрудно убедиться, что

Поэтому

и разложение для потенциала сводится к вкладу его первого члена:

Результат, как и должно быть, совпадает с . Но получен явно более громоздким путем, так как радиальная симметрия в распределении зарядов в ДСК учитывается не вполне адекватно.

2. Азимутально-симметричное распределение заряда в объеме шара радиуса

   1. Применение ССК

Согласно формулам и мультипольные моменты заданного распределения зарядов равны:

где

Их подстановка в приводит к мультипольному разложению потенциала следующего вида:

Если распределение заряда симметрично относительно отражения в плоскости, проходящей через центр шара и перпендикулярной полярной оси, формулы - дополнительно упрощаются. Действительно, при этом преобразовании симметрии

С другой стороны, согласно формуле Родрига ,

Вследствие этого, нечетные моменты обращаются в нуль:

и

2. Применение ДСК

Компоненты тензора мультипольного момента -го порядка определяется формулой:

в которой . В этом случае общий вид тензора определяется совокупностью единичных тензоров второго порядка и вектором направленным вдоль полярной оси. Как и ранее, тензор должен быть симметричен относительно произвольных перестановок индексов (см. ).

Очевидно, что

Компоненты момента первого порядка могут быть построены только из компонент. Поэтому

Для определения умножим обе стороны этого равенства на и свернем по значениям индекса. Таким путем получаем:

Компоненты , удовлетворяющие требованиям перестановочной симметрии, имеют структуру:

Умножая поочередно левую и правую части на и и сворачивая по индексам, получаем систему уравнений:

Из нее следует, что

По тем же причинам, что и в пункте a) настоящей задачи, вклад в мультипольное разложение потенциала обращается в нуль.

Аналогичным образом можно убедиться, что

а также

Полученные результаты позволяют заключать, что

Троеточием обозначены члены, приводящие к нулевым вкладам в мультипольном разложении потенциала.

Нетрудно видеть, что в рассматриваемом случае мультипольные разложения потенциала, полученные в ССК и ДСК полностью эквивалентны. Вместе с тем, применение ССК является более адекватным, поскольку изначально более полно учитывает симметрию в распределении зарядов.