Для студентов / Методички / (3)Методичка - ЕСС / Оператор Лапласа / (5)Радіальна складова оператора Лапласа в d-просторі

Оператор Лапласа в –мерном пространстве

Покажем, что радиальная составляющая оператора Лапласа в - мерном пространстве определяется выражением:

. (1)

Действительно, по определению, , где - произвольная скалярная функция. Чтобы найти , достаточно в качестве взять функцию, зависящую только от радиальной переменной: . В этом случае

, (2)

где - единичный орт, зависящий от совокупности угловых переменных: . Дивергенцию поля можно вычислить стандартным образом:

,

где - оператор набла, имеющий структуру . В этом подходе мы сталкиваемся с непростой проблемой вычисления . Чтобы избежать этих осложнений, воспользуемся интегральным определением дивергенции вектора:

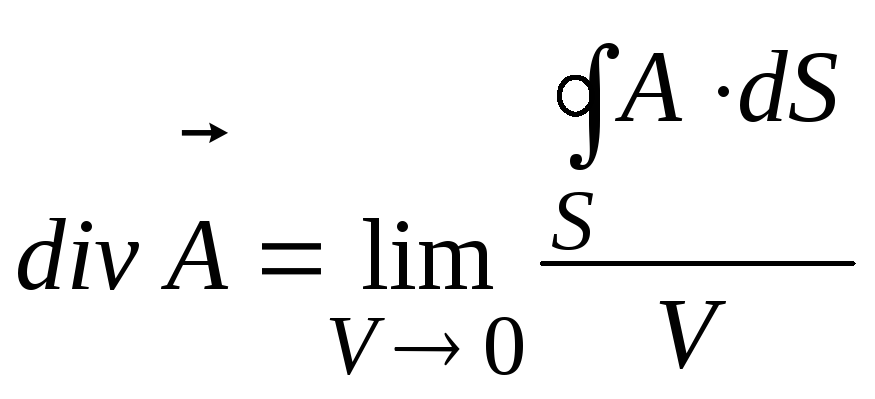, (3)

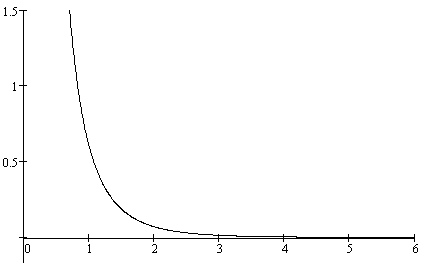
где - поверхность, охватывающая объем . Если вектор имеет радиальную структуру: , поверхность целесообразно выбрать в виде двух близких концентрических сфер с центром в начале координат, между которыми и находится точка (см. Рис.). В этом случае

,

.

Рис.

Учтено, что внешняя и внутренняя поверхности ориентированы в противоположных направлениях, и на каждой из них модуль вектора постоянен по величине. Величина объема, по сути, сводится к объему сферического слоя. Подставляя эти выражения в (3), находим:

. (4)

Так как и , то (1) немедленно следует из (4).

Отметим, что изложенный метод построения радиальной составляющей оператора Лапласа применим для произвольных значений , как целочисленных, так и дробных.

Корреляционная функция параметра порядка свободного поля в –мерном пространстве.

В Разделе … было показано, что КФ параметра порядка свободного поля в трехмерном пространстве совпадает с функцией Грина этого поля, которая

удовлетворяет уравнению:

(1)

Учтено, что в однородном и изотропном пространстве функция Грина зависит только от модуля радиус-вектора: , в связи с чем, оператор Лапласа заменен его радиальной составляющей .

При переходе к - мерному пространству общая структура уравнения сохраняется:

(2)

Замены трехмерных версий оператора Лапласа и дельта-функции их - мерными аналогами: - являются очевидными. Явный вид множителя перед дельта-функцией в (2) может быть получен из следующих соображений. При уравнение (2) переходит в уравнение Пуассона для потенциала единичного точечного заряда (, ). Нетрудно видеть, что , . Окружим заряд сферой радиуса и воспользуемся электростатической теоремой Гаусса-Остроградского ():

.

С учетом свойств симметрии эту формулу можно переписать в виде:

. (3)

Коэффициент , входящий в теорему Гаусса-Остроградского, как раз и является искомым коэффициентом, который должен стоять перед дельта-функцией в (2). Действительно, интегрируя обе части уравнения (1) по объему, включающему начало координат, находим:

.

Здесь мы использовали взаимосвязь потенциала и напряженности: .

Радиальная составляющая напряженности поля, очевидно, равна: . Отсюда и из (3) следует, что

. (4)

С учетом (1), уравнение (2) принимает вид:

. (5)

Переходя к мнимому аргументу: , мы получаем уравнение

(6)

которое может быть сведено к уравнению для цилиндрических функций:

(7)

Действительно, переходя к функции согласно уравнению

, (8)

находим:

. (9)

Уравнение (9) становится эквивалентным (7), если мы положим:

,

или . В этом случае

. (10)

Общее решение уравнения (7), имеет вид:

,

где – цилиндрические функции Бесселя.

Возвращаясь к переменной , отметим, что полученное решение уравнения (7) представляет собой цилиндрические функции Бесселя от мнимого аргумента . Функции Бесселя от мнимого аргумента имеют принципиально другое поведение по сравнению с функциями Бесселя действительного аргумента. Точнее, функции Бесселя мнимого аргумента монотонно возрастают от нуля до бесконечности либо убывают от бесконечности до нуля, а не осциллируют около нулевого значения с убывающей амплитудой, как функции Бесселя действительного аргумента. Убывающую на бесконечности функцию Бесселя мнимого аргумента принято называть функцией Макдональда , а возрастающую – функцией Ганкеля . 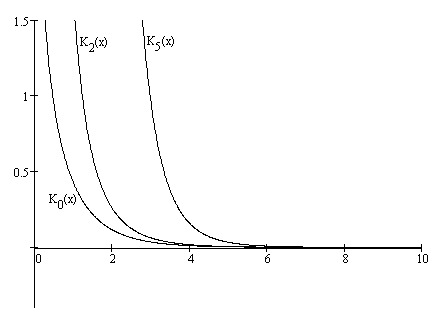Сравнительное поведение функции Бесселя действительного аргумента, функции Макдональда и функции Ганкеля одного порядка приведено на Рис.

Таким образом, решение уравнения (5) имеет вид:

, (11)

где – функция Макдональда (функция Бесселя мнимого аргумента).

Свойства функции Макдональда.

Функция Макдональда имеет следующее интегральное представление:

. (*)

Должны выполняться соотношения: , – гамма-функция.

Отсюда, дополняя контур интегрирования полуокружностью бесконечно большого радиуса, можно получить представление функции Макдональда в виде ряда. Интеграл вычисляется с помощью вычетов. Оценки показывают, что интеграл по упомянутой полуокружности равен нулю. Необходимо учесть, что функция имеет полюсы в точках , причем .

В результате получаем:

.

Данное разложение верно для нецелых , иначе подынтегральная функция в интеграле (*) имеет полюсы второго порядка.

Функция Макдональда обладает следующими свойствами:

1) является вещественной функцией ;

2) характеризуется асимптотиками:

(12)

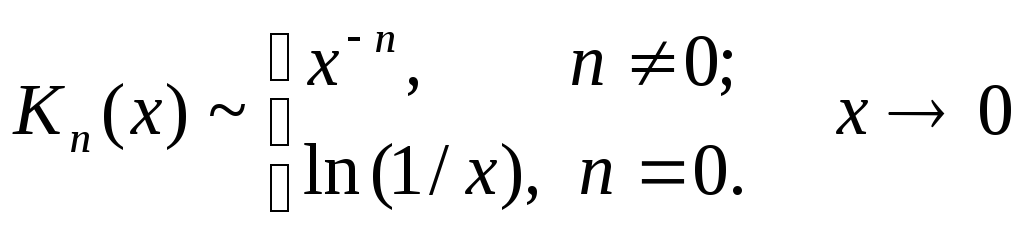и , (13)

3) функция Макдональда полуцелого порядка () выражается через элементарные функции:

, (14)

Сравнительное поведение функций Макдональда порядков и 5 приведено на Рис.

Свойства корреляционной функции параметра порядка свободного поля.

Воспользовавшись приведенными свойствами функции Макдональда (12) – (14), рассмотрим решения уравнения (5) в физически важных случаях .

а) Одномерный случай ():

Корреляционная функция имеет вид:

(15)

б) Двумерный случай ():

Корреляционная функция имеет вид:

. (16)

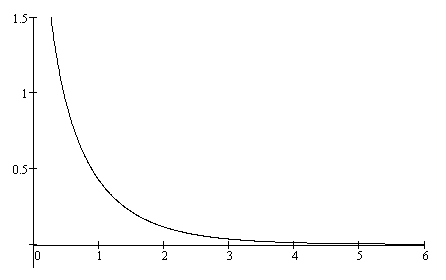
Она характеризуется экпоненциальным убыванием при и имеет логарифмическую особенность .

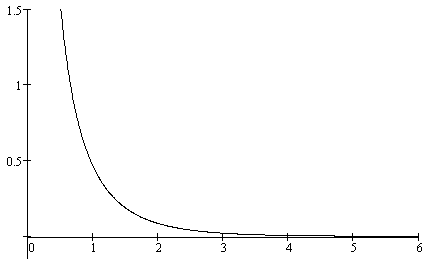
в) Трехмерный случай ():

Корреляционная функция имеет вид:

(17)

в) Четырехмерный случай ():

Корреляционная функция имеет вид:

. (18)