
Для студентов / Методички / (3)Методичка - ЕСС / Оператор Лапласа / (1)Визначення оператора Лапласа
.doc-
Визначення оператора Лапласа
За
визначенням, оператором Лапласа
![]() називають
скалярний добуток операторів набла
називають
скалярний добуток операторів набла
![]() :
:
![]() (1)
(1)
Розглянемо по черзі явний вигляд оператора Лапласа в декартовій, циліндричній і сферичній системах координат. Наприкінці цього розділу побудуємо оператор Лапласа в довільній криволінійній системі координат.
-
В декартовій системі координат (ДСК) оператор набла має структуру:
 .
Утворюючи згідно (1) скалярний
добуток,
знаходимо:
.
Утворюючи згідно (1) скалярний
добуток,
знаходимо:
![]() (2)
(2)
-
В циліндричній системі координат (ЦСК) оператор набла дорівнює
 .
Тут орти
.
Тут орти
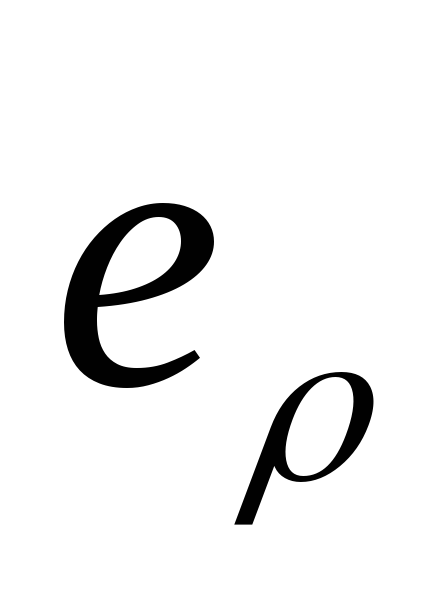 і
і
 є функціями кута
є функціями кута
 ,
що потрібно враховувати при побудові
оператора Лапласа. З цієї причини
потрібно більш детально розглянути
комбінації
,
що потрібно враховувати при побудові
оператора Лапласа. З цієї причини
потрібно більш детально розглянути
комбінації
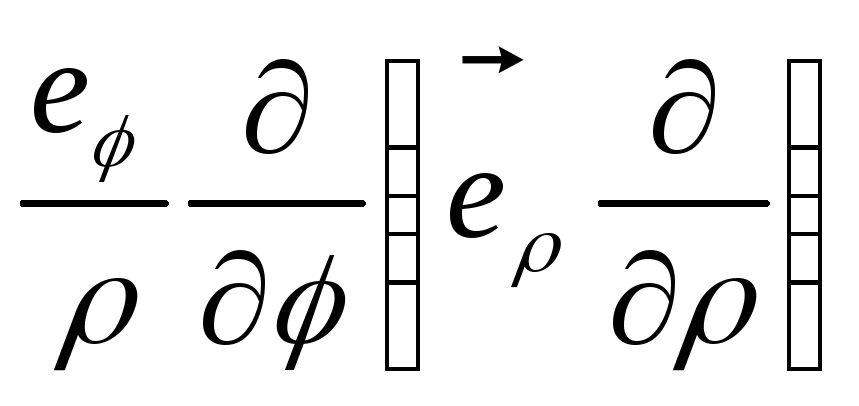 і
і
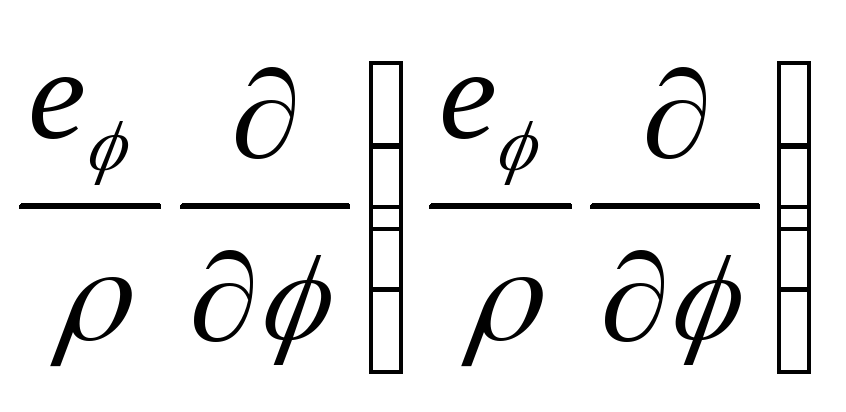 , які включають диференціювання по
, які включають диференціювання по
 .
Вирази, які стоять в дужках, потрібно
диференціювати як добутки двох функцій.
У такий спосіб знаходимо:
.
Вирази, які стоять в дужках, потрібно
диференціювати як добутки двох функцій.
У такий спосіб знаходимо:
![]() .
.
Враховуємо
ортогональність ортів циліндричної
системи координат
![]() ,
а також співвідношення
,
а також співвідношення
![]() ,
,
знаходимо:
![]() .
(3)
.
(3)
Так
само, враховуючи, що
![]() ,
отримуємо
,
отримуємо
![]() .
(4)
.
(4)
Всі інші скалярні комбінації є більш простими і в сукупності приводять до результату:
![]() .
.
Оскільки
![]() ,
,
то оператору Лапласа в ЦСК можна надати наступного остаточного вигляду:
![]() .
(5)
.
(5)
Складову
![]() називають
радіальною складовою оператора Лапласа.
називають
радіальною складовою оператора Лапласа.
-
В сферичній системі координат (ССК) оператор набла має структуру
![]() .
Всі орти ССК залежать
від
полярного
.
Всі орти ССК залежать
від
полярного
![]() і азимутального кутів
і азимутального кутів
![]() .
Оператор Лапласа будується за схемою,
цілком подібною до тієї, що була
використана для ЦСК. Похідні від ортів
за кутами
.
Оператор Лапласа будується за схемою,
цілком подібною до тієї, що була
використана для ЦСК. Похідні від ортів
за кутами
![]() і
і
![]() визначаються співвідношеннями:
визначаються співвідношеннями:
 (6)
(6)
З
цих співвідношень і умови ортогональності
![]() ,
,
![]() ,
отримуємо:
,
отримуємо:

Сумуючі останні три строчки, остаточно знаходимо:
![]() . (7)
. (7)
Оператор Лапласа представляють також у вигляді:
![]() (8)
(8)
де
![]() (9)
(9)
називають радіальною складовою, а
![]() (10)
(10)
кутовою складовою оператора Лапласа.
d)
В
довільній криволінійній системі
координат
![]() для побудови оператора Лапласа
скористаємось наступним співвідношенням:
для побудови оператора Лапласа
скористаємось наступним співвідношенням:
![]() ,
(11)
,
(11)
яке
встановлює
зв'язок між
![]() і операцією дивергенції від градієнта
довільної скалярної функції
і операцією дивергенції від градієнта
довільної скалярної функції
![]() .
Дивергенція векторного поля
.
Дивергенція векторного поля
![]() ,
як відомо, дорівнює
,
як відомо, дорівнює
![]() .
(12)
.
(12)
Тут
![]() є детермінантом від матриці
є детермінантом від матриці
![]() ,
утвореної компонентами метричного
тензора
,
утвореної компонентами метричного
тензора
![]() ,
,
![]() ,
де
,
де
![]() базисні
вектори. Контраваріантні компоненти
вектора
базисні
вектори. Контраваріантні компоненти
вектора
![]() є пов’язаними з його коваріантними
компонентами
є пов’язаними з його коваріантними
компонентами
![]() стандартним
чином:
стандартним
чином:
![]() ,
(13)
,
(13)
де
контраваріантні компоненти
![]() метричного
тензора пов’язані з
метричного
тензора пов’язані з
![]() співвідношенням:
співвідношенням:
![]() ,
,
в
якому
![]() є алгебраїчними доповненнями до елементів
є алгебраїчними доповненнями до елементів
![]() матриці
матриці
![]() .
Поєднуючи (12) і (13), знаходимо наступний
вигляд оператора Лапласа в криволінійній
системі координат:
.
Поєднуючи (12) і (13), знаходимо наступний
вигляд оператора Лапласа в криволінійній
системі координат:
![]()
або
![]() (14)
(14)
Можна впевнитись, що застосування (14) до циліндричної чи сферичної систем координат призводить до вже отриманих вище співвідношень (5) і (8).
Розглянемо тепер кілька прикладів застосування оператора Лапласа.
Задача
1.
Векторне поле
![]() описується формулою
описується формулою
![]() .
Знайти результат дії на нього оператора
Лапласа, тобто
.
Знайти результат дії на нього оператора
Лапласа, тобто
![]() .
.
Розв’язок:
Оскільки
поле
![]() задається
за допомогою змінних ЦСК, скористаємось
формулою (5) для оператора Лапласа. У
такий спосіб знаходимо:
задається
за допомогою змінних ЦСК, скористаємось
формулою (5) для оператора Лапласа. У
такий спосіб знаходимо:
![]() .
.
Перший
доданок перетворюється тривіальним
чином, оскільки орт
![]() не залежить від
не залежить від
![]() :
:
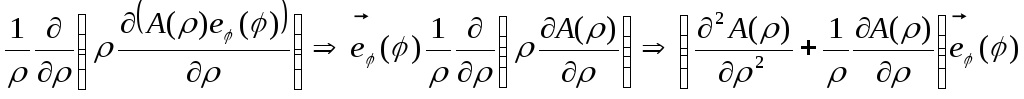 .
.
Враховуючи, що
![]() ,
а
,
а
![]() ,
,
знаходимо
![]() .
Таким чином,
.
Таким чином,
![]() .
(15)
.
(15)
Задача
2.
Векторне поле
![]() описується формулою
описується формулою
![]() .
Знайти результат дії на нього оператора
Лапласа, тобто
.
Знайти результат дії на нього оператора
Лапласа, тобто
![]() .
.
Розв’язок:
Неважко бачити, що
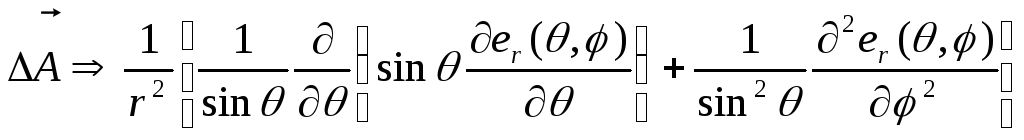 .
.
Згідно (6), перша строчка,
![]()
тому
![]() .
.
Ще раз диференціюючи за кутовими змінними і використовуючи значення похідних від ортів (див. (6)):
![]() ,
,
![]() ,
,
знаходимо:
![]() .
(16)
.
(16)
