Для студентов / Методички / (3)Методичка - ЕСС / Оператор Лапласа / (3)Собственные функции оператора Лапласа в ССК

3. Власні функції кутової складової оператора Лапласа

Функції , які задовольняють рівнянню:

(1)

і граничній умові

(2)

при довільних значеннях полярного кута , називаються сферичними функціями.

Іншими словами, є власними функціями кутової складової оператора Лапласа, які відповідають власному значенню: . Область задания функцій - одинична сфера, а умова (2) – є умовою неперервності.

Кожному власному значенню відповідає різних функций: , що вказує на -кратну вырожденность оператора . Приймається, що .

Сферичні функції задовольняють умові ортогональності:

(3)

яка є аналогом (). Тут - элемент тілесного кута.

Довільна функція , яка задається на одиничній сфері, розкладається в ряд:

, (4)

коефіцієнти якого визначаються рівнянням:

(5)

1. структура сферичних функцій:

Нормовані згідно (3) сферичні функції мають структуру:

(6)

де

(7)

а є приєднані поліноми Лежандра, які задовольняють рівнянню:

. (8)

Последнее непосредственно следует из при подстановке в него . В окремому випадку, коли , рівняння (8) переходить в рівняння:

(9)

для так званих поліномів Лежандра .

2. конкретний вигляд сферичних функцій:

При :

(10)

Для знаходження удобно скористатися производящей функцією поліномів Лежандра:

(11)

або формулою Родрига:

(12)

З них випливає, що

(13)

При :

(14)

При :

(15)

В загальному випадку,

(16)

4. Загальна структура розв’язку рівняння Лапласа в сферичних координатах

Нехай функція задовольняє рівнянню Лапласа:

. (17)

У згоді з (4) її можна представити у вигляді:

. (18)

Підставимо (18) в (17) і врахуємо рівняння (1) для сферичних функцій, а також незалежність сферичних функцій. У такий спосіб знаходимо наступне рівняння для коефіцієнтних функцій :

. (19)

В розгорнутому вигляді

. (20)

Оскільки коефіцієнти лінійного диференціального рівняння (20) є сингулярними при , його розв’язок необхідно шукати у вигляді . Неважко впевнитись, що показник задовольняє алгебраїчному рівнянню:

,

і дорівнює: , . Таким чином,

. (21)

Комбінуючи (18) і (21), остаточно знаходимо:

. (22)

Це і є загальний вигляд розв’язку рівняння Лапласа.

Розглянемо найпростіші часткові випадки:

1. Азимутально-симетричний розв’язок . Розв’язок рівняння Лапласа (17), який не залежить від , будемо називати азимутально-симетричним. В цьому випадку в (22) необхідно покласти 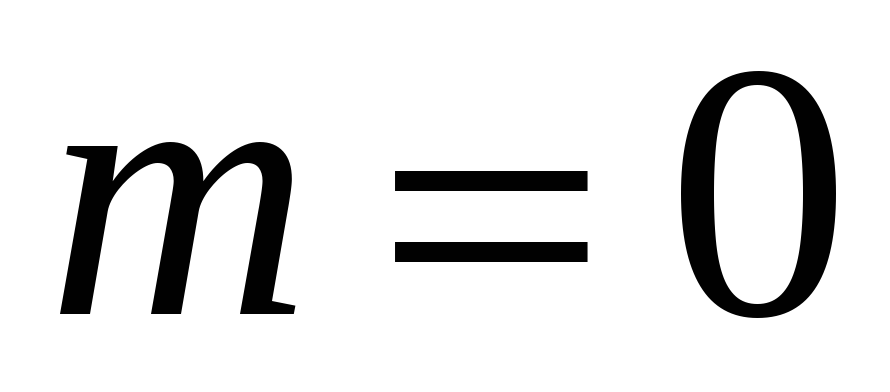і скористатись співвідношенням (10). Таким чином, знаходимо

. (23)

2. Центрально симетричний розв’язок . Із сферичних функцій тільки (див. (10) і (13)) не залежить від кутів і . Тому в (22) необхідно взяти тільки доданок з і :

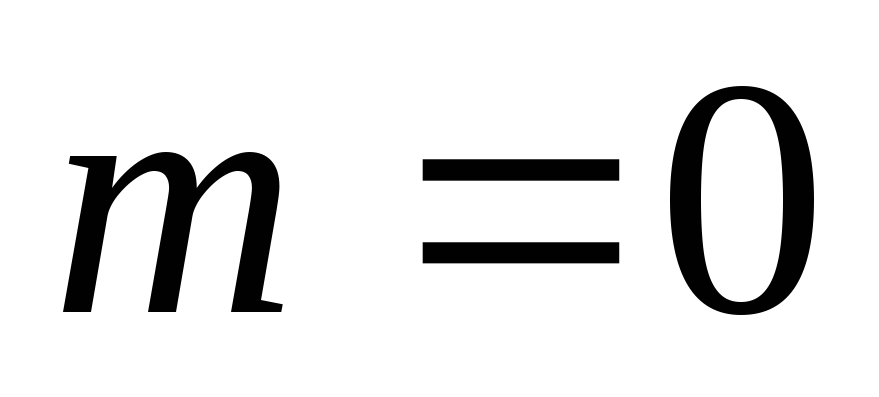. (24)