
Для студентов / Лекции / (2)ВЕД / Эквипотенциальные поверхности вблизи особых точек
.docЭквипотенциальные поверхности двух зарядов вблизи особых точек
-
Заряды
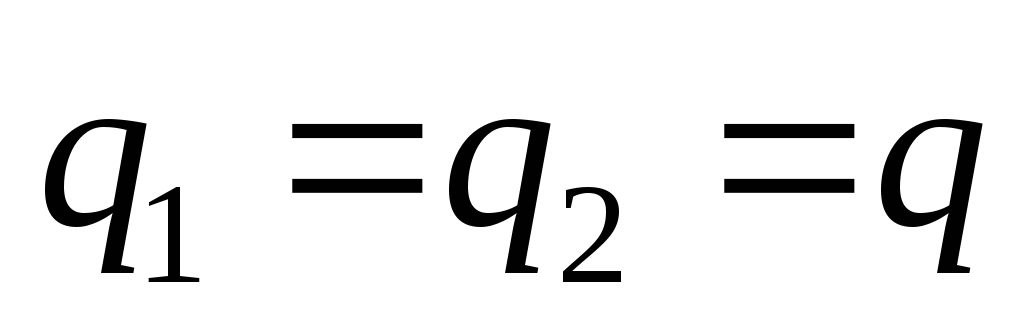 ,
,
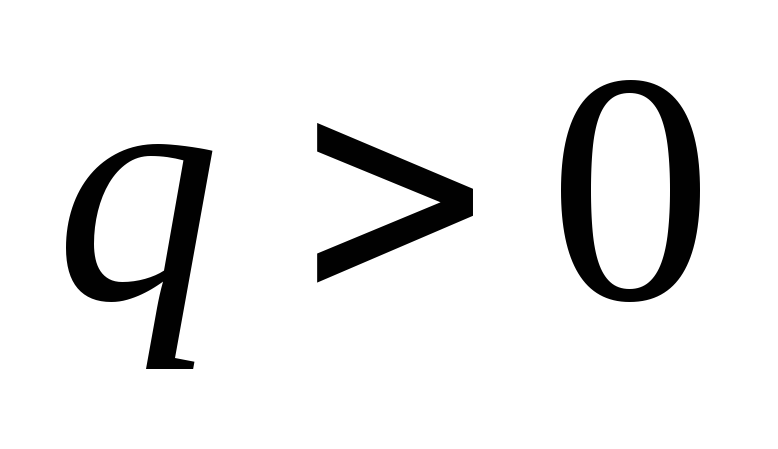 ,
находятся в точках
,
находятся в точках
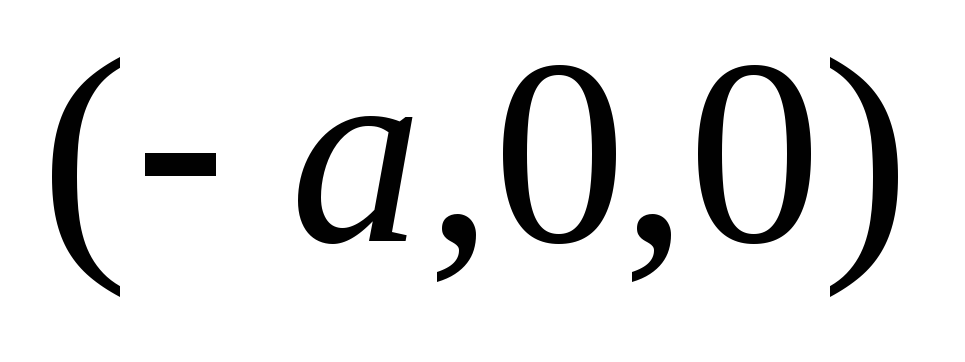 и
и
 .
Описать их эквипотенциальные поверхности.
.
Описать их эквипотенциальные поверхности.
Решение. Нетрудно видеть, что точка
![]() является особой. Это единственная точка,
в которой напряженность электрического
поля
является особой. Это единственная точка,
в которой напряженность электрического
поля
![]() ,
так что на произвольный заряд, помещенный
в эту точку, действующая сила будет
равна нулю .
,
так что на произвольный заряд, помещенный
в эту точку, действующая сила будет
равна нулю .
Рассмотрим потенциал поля в ближайшей
окрестности этой точки:
![]() .
Эквипотенциальные поверхности описываются
уравнениями:
.
Эквипотенциальные поверхности описываются
уравнениями:
![]() (1)
(1)
Фактически, достаточно описать форму
эквипотенциальных линий в плоскости
![]() .
Они описываются уравнением:
.
Они описываются уравнением:
![]() .
(2)
.
(2)
Эквипотенциальной поверхности (1) образуются вращением эквипотенциальных линий (2) вокруг оси х-ов.
При
![]() уравнение (2) упрощается и принимает
вид:
уравнение (2) упрощается и принимает
вид:
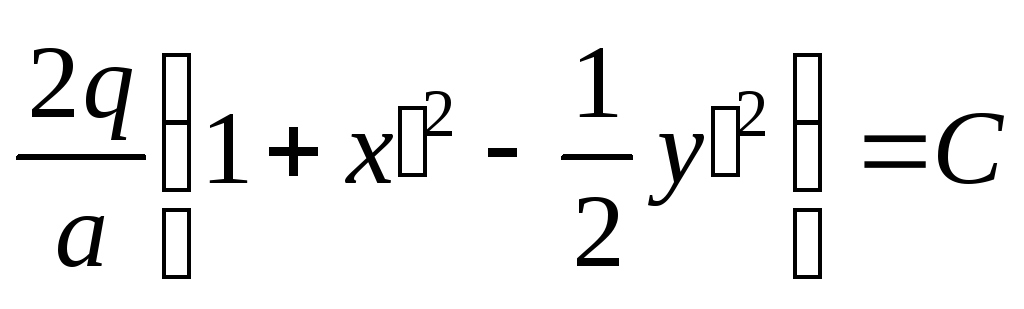 .
(3)
.
(3)
Значение потенциала в самой точке
![]() равно
равно
![]() .
Поэтому целесообразно представить:
.
Поэтому целесообразно представить:
![]() .
Тогда уравнение (3) естественно
представляется в виде:
.
Тогда уравнение (3) естественно
представляется в виде:
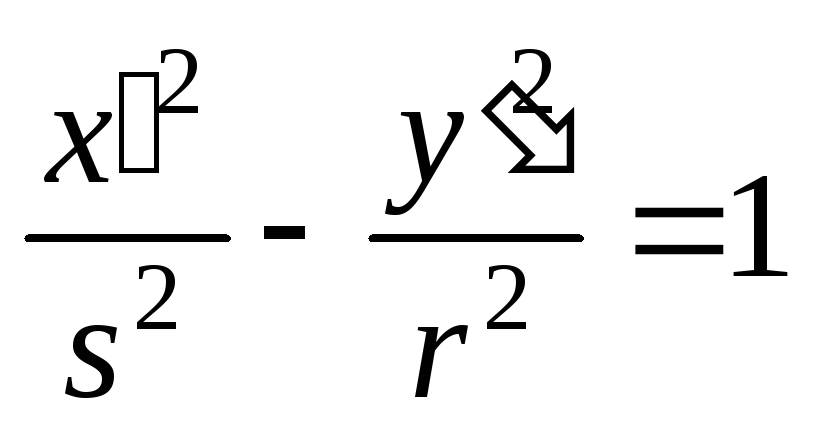 ,
если
,
если
![]() ,
,
и (4)
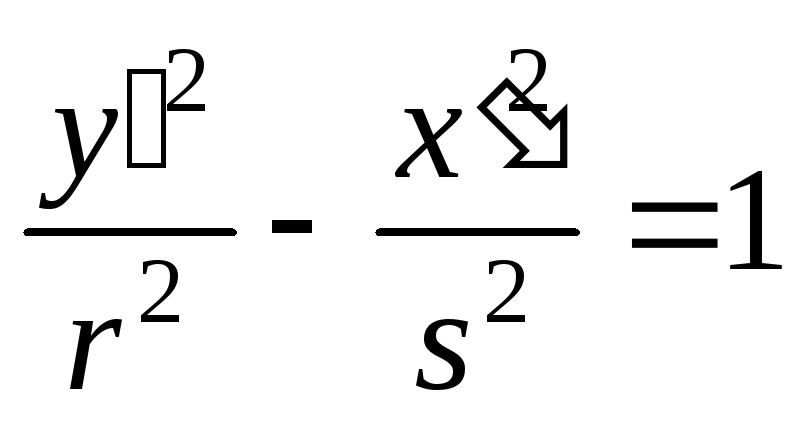 ,
если
,
если
![]() .
.
Здесь:
![]() ,
,
![]() .
Уравнениями (4) описываются гиперболы,
имеющие асимптоты:
.
Уравнениями (4) описываются гиперболы,
имеющие асимптоты:
![]() .
(5)
.
(5)
Области между асимптотами, расположенные
справа и слева от оси ординат, соответствуют
значениям
![]() ,
а расположенные выше и ниже оси абсцисс
-
,
а расположенные выше и ниже оси абсцисс
-
![]() .
.
-
Заряды
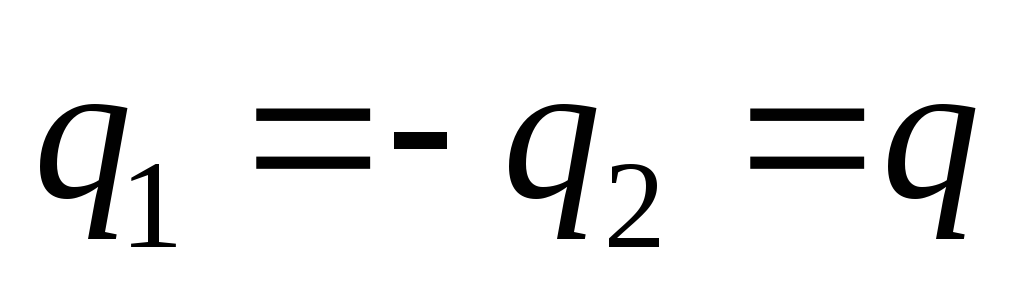 находятся
в точках
находятся
в точках
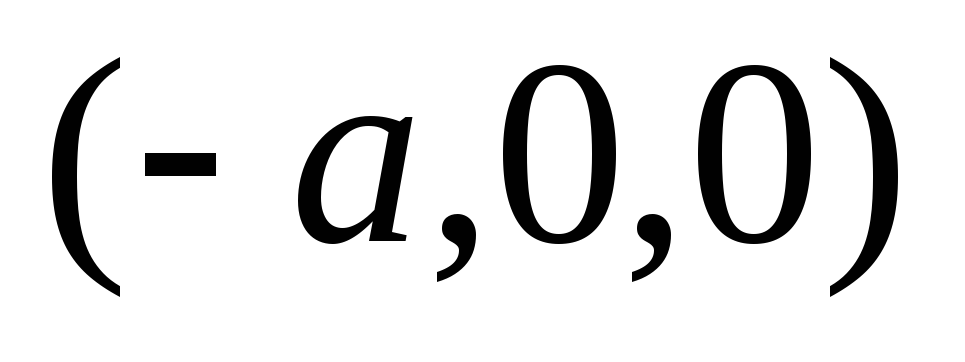 и
и
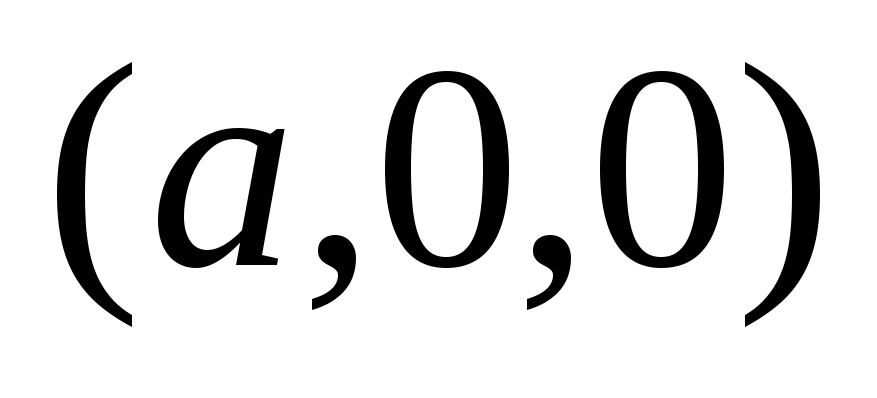 .
Описать их эквипотенциальные поверхности
окрестности эквипотенциальной
плоскости
.
Описать их эквипотенциальные поверхности
окрестности эквипотенциальной
плоскости
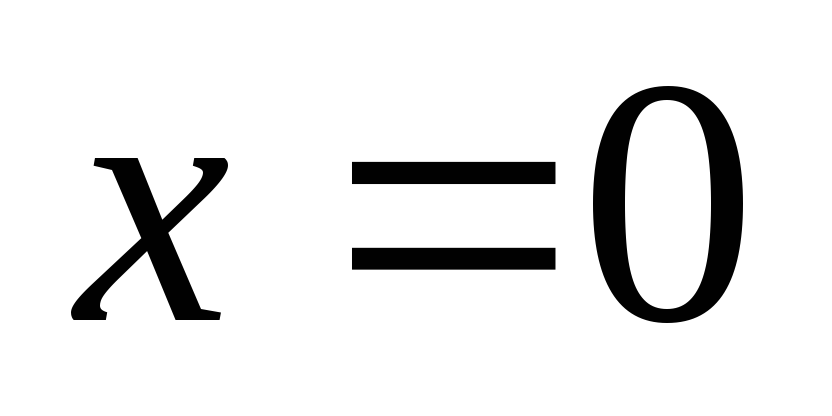 .
.
Решение. Эквипотенциальные линии
в окрестности прямой
![]() описываются уравнением:
описываются уравнением:
![]() .
(6)
.
(6)
Нетрудно видеть, что в полуплоскости
![]() постоянная
постоянная
![]() должна быть отрицательна:
должна быть отрицательна:
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() .
(7)
.
(7)
При
![]() формула (7) может быть упрощена путем
разложения в ряд по степеням
формула (7) может быть упрощена путем
разложения в ряд по степеням
![]() :
:
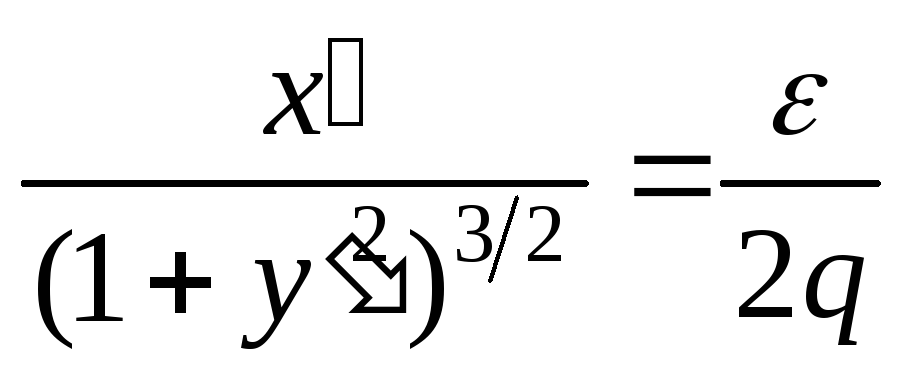 .
.
Отсюда следует, что
 .
(6)
.
(6)
Область применимости формулы (6) определяется неравенствами:
![]() .
(7)
.
(7)
Как и должно быть, производная функции
![]() в
точке
в
точке
![]() обращается в бесконечность.
обращается в бесконечность.
Эквипотенциальные линии в области
![]() (
(![]() )
могут быть получены путем зеркального
отражения линий, описываемых уравнением
(6), относительно линии
)
могут быть получены путем зеркального
отражения линий, описываемых уравнением
(6), относительно линии
![]() .
.
