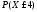3. Предельная теорема Пуассона
Предельная
теорема Пуассона позволяет вычислить
вероятность того, что число успехов
в схеме Бернулли будет равно m
, при

 ,
где
,
где
 .
.
Задание 4. Найти вероятность того, что в 500 испытаниях успех появится 5 раз, если вероятность успеха в одном испытании p равна 0,025.
Решение.
a.
Сначала выполните задание непосредственным
вычислением
 .
.
1.

2.

Excel позволяет вычислить искомую вероятность применением или формулы ПУАССОН или формулы БИНОМРАСП.
Заполните ячейки исходными данными, как показано на рис. 23.

Рис. 23. Исходные данные: n – число испытаний, p – вероятность успеха, m – число успехов, λ – параметр распределения Пуассона

Рис.
24. В ячейке E66
выполнены вычисления непосредственно
по формуле

b. Для вычисления искомой вероятности по формуле ПУАССОН(x; среднее; интегральная) в категории Статистические библиотеки функций выберите функцию ПУАССОН

Рис. 25. Диалоговое окно функции ПУАССОН с заполненными полями ввода (в поле Интегральная введен 0, чтобы получить значение функции вероятности)

Рис. 26. В ячейке E68 резльтаты вычисления искомой вероятности по формуле ПУАССОН
c. Для вычисления требуемой вероятности по формуле
БИНОМРАСП(число_успехов; число_ испытаний; вероятность_успеха; интегральная) в категории Статистические библиотеки функций выберите функцию БИНОМРАСП

Рис. 25. Диалоговое окно функции БИНОМРАСП с заполненными полями ввода (в поле Интегральная введен 0, чтобы получить значение функции вероятности)

Рис. 26. В ячейке E70 резльтаты вычисления искомой вероятности по формуле БИНОМРАСП
Сравните результаты вычислений и сделайте выводы.
Приложение 1.
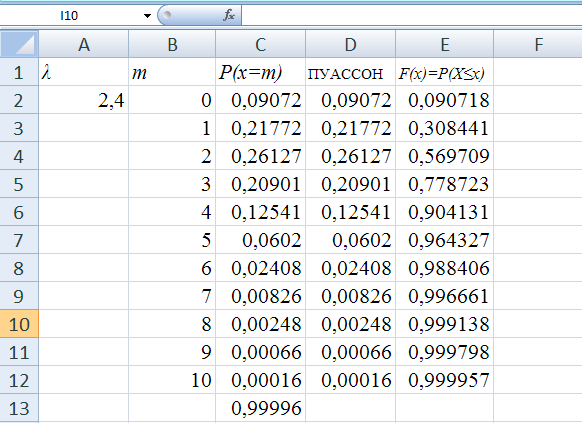





Приложение 2.
Отчет
Лабораторная работа №3. Распределение Пуассона (с параметром λ).
Предельные теоремы в схеме испытаний Бернулли.
Группа 190-1. Мельников Иван Л. Вариант №5.
Отчет должен содержать тексты заданий, исходные данные и распечатки вычислений в Excel как показано в приложении 1.
Дата сдачи работы:
Проверил:
Приложение 3.
Задание
1.
Целочисленная
величина X
имеет распределение Пуассона с
параметром λ
= 2,4. Построить ряд распределения
 и функцию распределения
и функцию распределения случайной величиныX.
Найти математическое ожидание, дисперсию,
среднее квадратическое отклонение
случайной величина.
случайной величиныX.
Найти математическое ожидание, дисперсию,
среднее квадратическое отклонение
случайной величина.
Найти
вероятности:
 ,
, ,
, ,
, ,
,
 .
.
|
Варианты |
λ |
|
|
|
|
|
|
1; 11; 21 |
2 |
|
|
|
|
|
|
2; 12; 22 |
2,8 |
|
|
|
|
|
|
3; 13; 23 |
3 |
|
|
|
|
|
|
4; 14; 24 |
3,5 |
|
|
|
|
|
|
5; 15; 25 |
4 |
|
|
|
|
|
|
6; 16; 26 |
4,3 |
|
|
|
|
|
|
7; 17; 27 |
5 |
|
|
|
|
|
|
8; 18; 28 |
5,7 |
|
|
|
|
|
|
9; 19; 29 |
6,1 |
|
|
|
|
|
|
10; 20 |
7 |
|
|
|
|
|
Задание 2. Вероятность появления события A при одном испытании равна p = 0,37. Найти вероятность того, что при n = 100 испытаниях событие A появится m = 35 раз.
|
Варианты |
n |
p |
m |
|
1; 11; 21 |
100 |
0,4 |
35 |
|
2; 12; 22 |
120 |
0,49 |
58 |
|
3; 13; 23 |
110 |
0,35 |
41 |
|
4; 14; 24 |
130 |
0,45 |
59 |
|
5; 15; 25 |
140 |
0,52 |
74 |
|
6; 16; 26 |
120 |
0,6 |
65 |
|
7; 17; 27 |
110 |
0,47 |
52 |
|
8; 18; 28 |
100 |
0,42 |
48 |
|
9; 19; 29 |
140 |
0,39 |
54 |
|
10; 20 |
100 |
0,57 |
54 |
Задание 3. Вероятность появления события A при одном испытании равна p = 0,37. Найти вероятность того, что при n = 100 испытаниях событие A появится от m1 = 35 до m2 = 40 раз.
|
Варианты |
n |
p |
m1 |
m2 |
|
1; 11; 21 |
100 |
0,4 |
34 |
44 |
|
2; 12; 22 |
120 |
0,49 |
56 |
62 |
|
3; 13; 23 |
110 |
0,35 |
38 |
45 |
|
4; 14; 24 |
130 |
0,45 |
56 |
67 |
|
5; 15; 25 |
140 |
0,52 |
71 |
80 |
|
6; 16; 26 |
120 |
0,6 |
67 |
75 |
|
7; 17; 27 |
110 |
0,47 |
45 |
54 |
|
8; 18; 28 |
100 |
0,42 |
45 |
53 |
|
9; 19; 29 |
140 |
0,39 |
54 |
65 |
|
10; 20 |
100 |
0,57 |
54 |
71 |
Задание 4. Найти вероятность того, что в n = 500 испытаниях успех будет равно m = 5, если вероятность успеха в одном испытании p равна 0,025.
|
Варианты |
n |
p |
m |
|
1; 11; 21 |
500 |
0,04 |
3 |
|
2; 12; 22 |
620 |
0,03 |
5 |
|
3; 13; 23 |
410 |
0,035 |
4 |
|
4; 14; 24 |
530 |
0,045 |
5 |
|
5; 15; 25 |
640 |
0,055 |
4 |
|
6; 16; 26 |
720 |
0,06 |
5 |
|
7; 17; 27 |
810 |
0,07 |
5 |
|
8; 18; 28 |
600 |
0,04 |
4 |
|
9; 19; 29 |
540 |
0,029 |
5 |
|
10; 20 |
900 |
0,053 |
5 |