
- •Тема 2. Элементы аналитической геометрии на плоскости.
- •Основные формулы аналитической геометрии.
- •Примеры решения задач.
- •Вопросы для самопроверки.
- •Тема 3. Основы векторной алгебры.
- •3.1 Операции над векторами.
- •Векторное произведение
- •Смешанное произведение.
- •3. 2 Примеры решения задач.
- •3. 3 Вопросы для самопроверки.
- •Тема 4. Введение в анализ.
- •Понятие предела.
- •4.2 Способы раскрытия неопределённостей вида и .
- •Первый и второй замечательные пределы.
- •Непрерывность функции. Точки разрыва.
- •Вопросы для самопроверки.
- •Тема 5. Производная и дифференциал функции одного аргумента.
- •5. 1 Определение производной, дифференциала.
- •Основные правила дифференцирования.
- •Примеры решения задач.
- •Вопросы для самопроверки.
- •Тема 6. Приложения производной к исследованию поведения функции и построению графика и к другим задачам.
- •План исследования функции и построения графика.
- •Использование производной в задачах прикладного характера.
- •План действий при решении задач прикладного характера.
- •Нахождение наибольшего и наименьшего значения функции на отрезке.
- •Вопросы для самопроверки.
3. 2 Примеры решения задач.
Задача
5.
Даны координаты вершин пирамиды ABCD:
А (2; 1; 0), B
(3; -1; 2), С (13; 3;
10), D
(0; 1; 4). Требуется: 1) записать векторы
![]() и
и
![]() в системе орт
в системе орт
![]() и найти модули этих векторов; 2) найти
угол между векторами
и найти модули этих векторов; 2) найти
угол между векторами![]() и
и ![]() ;
3) найти проекцию
вектора
;
3) найти проекцию
вектора
![]() на вектор
на вектор ![]() ;
4) найти площадь грани
ABC;
5) найти объем
пирамиды ABCD.
;
4) найти площадь грани
ABC;
5) найти объем
пирамиды ABCD.
Решение.
I.
Произвольный вектор а может быть
представлен в системе орт i,
j,
k
![]() следующей формулой;
следующей формулой;
![]() (1)
(1)
где
ах,
ау,
аг
— проекции вектора
а на координатные оси Ох,
Оу и Oz,
а
![]() —
единичные векторы, направления
которых совпадают с положительным
направлением осей Ох,
Оу и Oz.
Если даны точки
—
единичные векторы, направления
которых совпадают с положительным
направлением осей Ох,
Оу и Oz.
Если даны точки ![]() и
и ![]() то проекции вектора
то проекции вектора ![]() на координатные оси находятся по
формулам:
на координатные оси находятся по
формулам:
![]()
![]()
![]() (2)
(2)
Тогда
![]() (3)
(3)
Подставив
в (3) координаты точек A
и В, получим вектор ![]()
![]()
Аналогично, подставляя в (3) координаты точек А и С, находим
![]()
Подставив
в (3) координаты точек А
и
D,
находим вектор
![]() :
:
![]()
Если
вектор ![]() задан формулой (1), то его модуль
вычисляется по формуле
задан формулой (1), то его модуль
вычисляется по формуле
![]() (4)
(4)
Применяя (4), получим модули найденных векторов:
![]()
![]() ,
,
![]()
2.
Косинус угла между двумя векторами
равен скалярному произведению этих
векторов, деленному на произведение
их модулей. Находим скалярное произведение
векторов ![]() и
и ![]() :
:
![]()
Модули
этих векторов уже найдены:
![]() ,
,
![]() Следовательно,
Следовательно,
![]()
![]() ¢.
¢.
3.
Проекция вектора
![]() на вектор
на вектор ![]() равна
скалярному произведению этих векторов,
деленному на модуль вектора
равна
скалярному произведению этих векторов,
деленному на модуль вектора ![]() :
:
![]()
4.
Площадь грани ABC
равна половине площади
параллелограмма, построенного на
векторах ![]() и
и
![]() .Обозначим векторное
произведение вектора
.Обозначим векторное
произведение вектора ![]() на вектор
на вектор ![]() через вектор
через вектор ![]() .
Тогда, как известно, модуль вектора
.
Тогда, как известно, модуль вектора ![]() выражает собой площадь параллелограмма,
построенного на векторах
выражает собой площадь параллелограмма,
построенного на векторах ![]() и
и ![]() ,
а площадь грани ABC
будет равна половине
модуля вектора
,
а площадь грани ABC
будет равна половине
модуля вектора![]() :
:
_
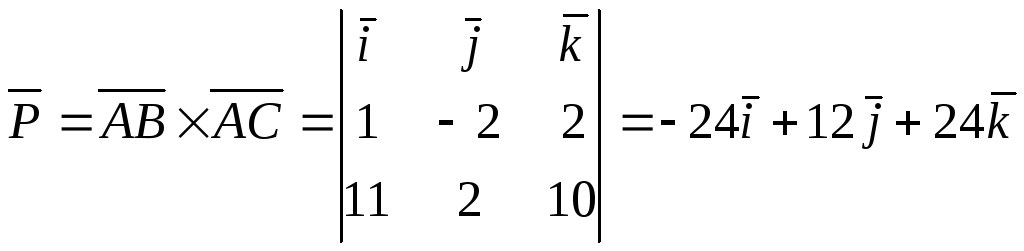
![]()
![]() кв. ед.
кв. ед.
5. Объем
параллелепипеда, построенного на трех
некомпланарных векторах, равен
абсолютной величине их смешанного
произведения. Вычислим смешанное
произведение ![]()

Следовательно, объем параллелепипеда равен 144 куб. ед., а объем заданной пирамиды ABCD равен 24 куб. ед.
3. 3 Вопросы для самопроверки.
Дайте определение вектора.
Какие векторы называются равными?
Геометрическое и аналитическое толкование координат вектора.
Запишите модуль вектора между координатами.
Как выполняется сложение, вычитание, умножение вектора на число геометрически (рисунком) и аналитически (формулой).
Дайте определение базису пространства.
Запишите скалярное произведение двух векторов в векторной форме и между координатами перемножаемых векторов. То же для векторного и смешанного произведения.
Условия коллинеарности и компланарности векторов в векторной и координатной форме.
