Указания к выполнению контрольной работы №1

Тема 2. Элементы аналитической геометрии на плоскости.

Ефимов, гл 1-3, 4-6

Данко, гл. 1, §1-5.

1. Основные формулы аналитической геометрии.

1.- длина отрезка между точкамии

2. ;- координаты точки деления отрезка в данном отношении.

| | | | |

-отношение величины отрезка от начала отрезка т. M₁ до делящей т. C к величине отрезка от делящей точки C до конца отрезка M₂ .

3. - уравнение прямой линии с угловым коэффициентом.

- угловой коэффициент прямой.

- тангенс угла между двумя прямыми.

-угол между двумя прямыми.

- условие | | двух прямых.

- условие  двух прямых.

yy

b

x x0 0

рис 1. рис 2.

4. - уравнение пучка прямых.

y

- центр пучка.

M₀

х

0

рис 3.

5. - уравнение прямой, проходящей через две точки и

6. - уравнение прямой, проходящей через точкупараллельно вектору+

y

x

0

рис 4.

7. - уравнение прямой, проходящей через т., перпендикулярно вектору.

y

x

0

М₀

рис. 5

8. - общее уравнение прямой- уравнение первой степени с двумя неизвестными.

9. - уравнение в отрезках на осях.

y

b

0ax

рис. 6

10. параметрические уравнения прямой.



, t- переменный параметр.

11.- уравнение окружности с центром в т.O (0;0) и радиусом r. ( рис. 7 )

рис. 7

- уравнение окружности со смещённым центром . (рис. 8)

12. Каноническое уравнение эллипса.

- уравнение эллипса с центром в начале координат.

- уравнение эллипса со смещённым центром в т. O₁(x₀,y₀).

13. Каноническое уравнение гиперболы.

- каноническое уравнение гиперболы с центром в начале координат.

- уравнение гиперболы со смещённым центром O₁ ( x₀, y₀).

14. Каноническое уравнение параболы.

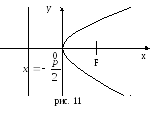
- каноническое уравнение параболы с вершиной в т. O (0,0).

- уравнение директрисы.

- уравнение параболы со смещённой вершиной в т. O₁ (x₀,y₀)