
Потоки в сетях.
Варианты задач:
1) Пусть каждой дуге графа приписана не
только пропускная способность
![]() ,
- верхняя граница потока через дугу (
,
- верхняя граница потока через дугу (
![]() )
по так же
)
по так же
![]() - нижнюю границу потока через дугу
Если задать стоимость единицы потока
, протекающего по дуге, то возникает
задача нахождения допустимого потока
минимальной стоимости (от s
и t).
- нижнюю границу потока через дугу
Если задать стоимость единицы потока
, протекающего по дуге, то возникает
задача нахождения допустимого потока
минимальной стоимости (от s
и t).
2) Ищутся max потоки между
каждой парой![]() вершин. Она может быть решена как
вершин. Она может быть решена как
![]() « отдельных » от s и t
задач, но это трудоёмкий процесс. При
нахождении
« отдельных » от s и t
задач, но это трудоёмкий процесс. При
нахождении
путей между каждой парой вершин
графа не обязательно решать каждую
задачу индивидуально .![]()
3)Если вместо 1 источника и 1 стока рассмотреть несколько источников и стоков, причем между различными источниками и стоками протекают потоки различных продуктов, то имеем задачу с многопродуктовым потоком.
Пропускная способность
![]() дуги (
дуги (![]()
![]() )
ограничена для суммы всех видов продуктов
через эту дугу.
)
ограничена для суммы всех видов продуктов
через эту дугу.
4) Если исходить оттого, что поток на входе = потоку на выходе, то выходит поток дуги
= входному потоку, умноженному на некоторое неотрицательное число, то получим задачу о потоках с «выигрышами». В такой задаче потоки могут и « порождаемые» и «погашаемые» самим графом, а поток, входящий в S и потом покидающий t, могут изменяться совершенно независимо.
Задачи о max потоке
Рассмотрим граф G=(X,A)
с пропускными способностями дуг
![]() ,
источником S и стоком t.
S,t
,
источником S и стоком t.
S,t![]() X.Множество
чисел
X.Множество
чисел
![]() ,определенных
на дугах (
,определенных
на дугах (![]() ,
называется потоками в дугах, если
выполняется условие
,
называется потоками в дугах, если
выполняется условие![]()
![]() :
:![]() -
-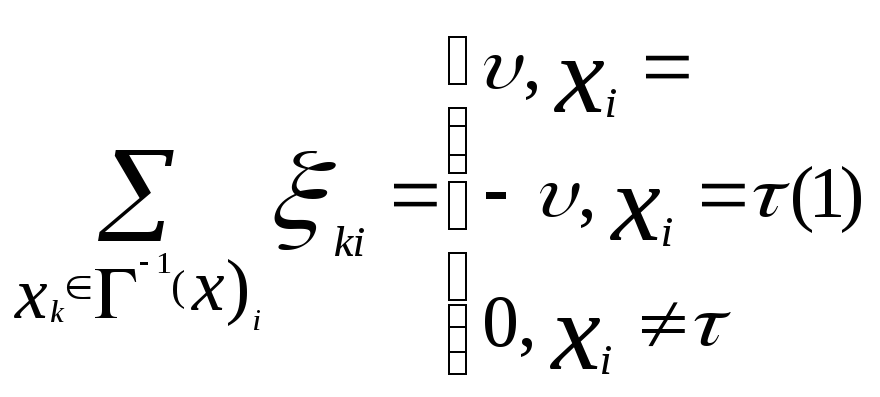 и
и
![]()
-
– уравнение сохранения потока : Поток, втекающий в вершину, равен потоку, вытекающему из вершины за исключением источника (s) и стока (t).Для S-S-сетевое вытекание и t- приток велиены,V соответственно.
-
– ограниченны на пропускные способности для каждой дуги G.Задача: найти множество потоков по дугам, чтобы величина V=
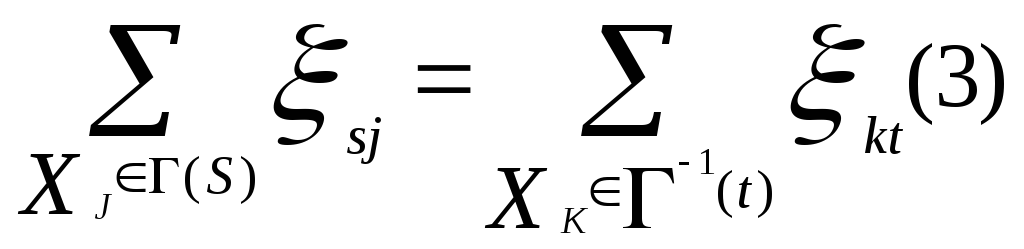
 была
максимальной.
была
максимальной.
Теорема Форда-Фацкерсона:
(о максимальном потоке и максимальном разрезе).
Величина максимального потока из s
в t равна величине min
разреза (![]() ),
отделяющего s от t.
Разрез
),
отделяющего s от t.
Разрез![]() отделен s от t
, если S
отделен s от t
, если S![]()
![]() и
t
и
t
![]() .Величиной
такого разреза называется сумма
пропускных способностей всех дуг из g,
начальные ве
.Величиной
такого разреза называется сумма
пропускных способностей всех дуг из g,
начальные ве
![]()
Вершины которых лежат в
![]() ,
а конечные в
,
а конечные в
![]() ,т.е.
,т.е.
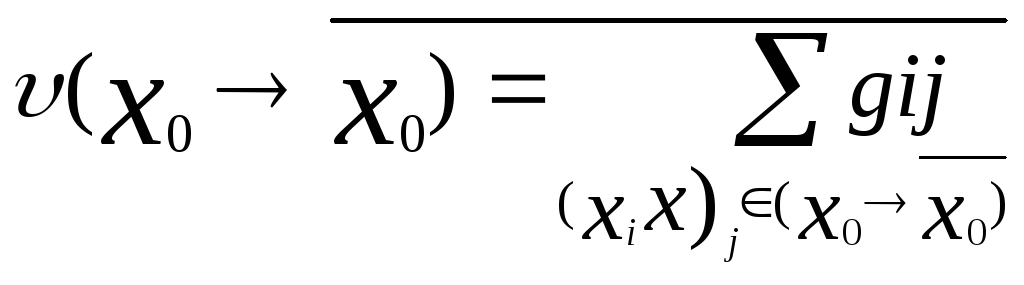 )
Минимальный разрез (
)
Минимальный разрез (
![]() )-
это разрез с наименьшим таким значением.
)-
это разрез с наименьшим таким значением.
![]()
Доказательство.
Очевидно, что max поток из
s в t не
может быть больше, чем v
(
![]() ) т.е. всякая цель из s в
t проходит хотябы через
1 дугу данного разреза. Поэтому достаточно
установить существование потока с таким
значением. Допустим , что поток задается
м-мерным вектором
) т.е. всякая цель из s в
t проходит хотябы через
1 дугу данного разреза. Поэтому достаточно
установить существование потока с таким
значением. Допустим , что поток задается
м-мерным вектором
![]() . и определим разрез (
. и определим разрез (
![]() )
рекурсивным применением нижеуказанного
шага б)
)
рекурсивным применением нижеуказанного
шага б)
а ) Начать, пологая
![]() {
s}.
{
s}.
б) Если![]() и, кроме того,
и, кроме того,
![]()
![]() или
или
![]() ,
то включить
,
то включить
![]() во
множество
во
множество
![]() и повторять этот шаг до тех пор, пока
множество
и повторять этот шаг до тех пор, пока
множество
![]() нельзя будет рассмотреть дальше.
нельзя будет рассмотреть дальше.
![]()
Теперь могут возникнуть 2 случая в
зависимости от того, будет ли t![]()
![]() или t
или t![]() .
.![]()
.
Случай (1) , t![]() ;
В соответствии с шагом б) отношение t
;
В соответствии с шагом б) отношение t![]() означает следующее: существует такое
« неориентирование « цель, ведущее из
s в t, что
для каждой дуги (
означает следующее: существует такое
« неориентирование « цель, ведущее из
s в t, что
для каждой дуги (![]() ),
используется только в прямом направлении
( прямой дуги ),
),
используется только в прямом направлении
( прямой дуги ),![]() а для каждой дуги (
а для каждой дуги (
![]() ),
используется только в обратном
направлении, т.е. от
),
используется только в обратном
направлении, т.е. от
![]() к
к
![]() )(
)(
обратной дуги ),
![]() ( эта цепь называется аугументами
augmen - увеличение ) (
( эта цепь называется аугументами
augmen - увеличение ) (
цепью потока.
Пусть
![]() =
min [
=
min [![]() ]
для прямой дуги (
]
для прямой дуги (
![]() ),
),
(![]() )
)
![]()
![]() ) для обратной дуги (
) для обратной дуги (![]()
![]()
(![]()
![]() )
)
(и
![]()
![]()
Если теперь величину
![]() прибавить к потоку во всех прямых дугах
и вычесть из всех обратных дугах цепи
, то в результате получится новый
допустимый поток, на
прибавить к потоку во всех прямых дугах
и вычесть из всех обратных дугах цепи
, то в результате получится новый
допустимый поток, на
![]() единиц больший, чем предыдущий. Это
очевидно в силу того, что прибавление
величины
единиц больший, чем предыдущий. Это
очевидно в силу того, что прибавление
величины
![]() к потоку в прямых дугах не может
привести к пресыщению ни одной из
пропускных способностей этих дуг (т.к.
к потоку в прямых дугах не может
привести к пресыщению ни одной из
пропускных способностей этих дуг (т.к.![]() ) , а вычитание
) , а вычитание
![]() из потока в обратных дугах не может
сделать поток в этих дугах отрицательным
( т.к.
из потока в обратных дугах не может
сделать поток в этих дугах отрицательным
( т.к.
![]()
Используя наш направленный поток,
можно затем повторить шаги а) и б) и
опредилив новый разрез(![]() ) , повторить
) , повторить
Случай (2), t![]() (т.е.t
(т.е.t![]() ).
В соответствии с шагом (
).
В соответствии с шагом (![]() )
)
![]() и
и
![]() Следовательно
Следовательно
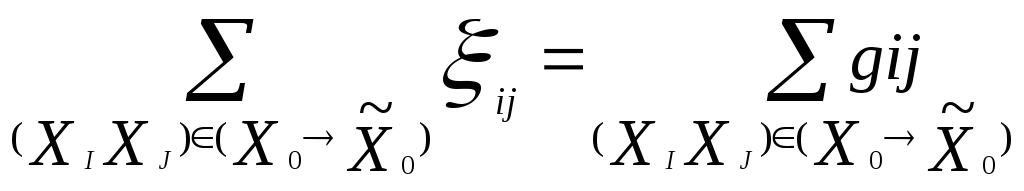 и
и
![]() величин потока , а именно
величин потока , а именно
![]()
![]() равна величине разреза (
равна величине разреза (![]() .
.
Т.к. в случае (1) поток все время
увеличивается, по крайней мере, на 1, то
при целочисленности всех gij
max и поток направляется
за конечное число шагов – как только
возникает случай (2). Этот поток будет
равен величине текущего разреза (![]() )
, который будет равен минимальному
разрезу. Теорема доказана.
)
, который будет равен минимальному
разрезу. Теорема доказана.
Алгоритм начинает работу с произвольного допустимого потока ( можно взять и 0-й поток), затем стремится увеличить величину потока с помощью систематического поиска всех возможных аугментальных целей потока от s к t. Поиск аугментальной цели осуществляется с помощью расставленных пометок в вершинах графа. Поэтому указывают, вдоль каких дуг может быть увеличен поток и на сколько.
Как только найдена одна из таких цепей, поток вдоль нее увеличивают до max значения, а пометки в вершинах стираются и вновь полученный поток используется в качестве исходного при новой расстановке пометок. Алгоритм работу заканчивает и дает max поток, если нельзя найти ни 1 аугментальную цель.
