
- •Моделирование работы светофора с нечеткой логикой
- •Введение
- •Способы организации движения
- •Недостатки существующих моделей
- •Цель работы
- •Постановка задачи
- •Математический аппарат
- •Операции с множествами
- •Нечеткая переменная
- •Лингвистическая переменная
- •Функции принадлежности
- •Логический вывод
- •Алгоритмы вывода
- •Алгоритм Мамдани
- •Рассматриваемый
- •Потоки транспортных средств
- •Пример распределения потока №1
- •Схема работы нечеткого светофора
- •Модуль светофора
- •Функции принадлежности для очередей
- •Базы правил
- •Организация движения на площади Горская
- •Организация работы нечёткого светофора
- •Пропускные способности
- •Анализ результатов
- •Источники информации

Моделирование работы светофора с нечеткой логикой

Введение
Не секрет, что проблема организации дорожного движения является на сегодня одной из самых острых. Важным фактором того, насколько быстро вы доберетесь в городе до нужного места, является работа светофора. И зачастую, именно его неэффективная работа является причиной городских “пробок”.
Мы взялись за решение данной проблемы не только из-за её актуальности, но и из-за того, что с этой проблемой приходилось сталкиваться и нам самим.

Способы организации движения
Светофор PCT типа
«Зеленая Волна»
Светофор VA типа
Принципиально новый подход:
Светофор управляемый нечеткой логикой

Недостатки существующих моделей
Большинство существующих на сегодняшний день моделей обладают следующими недостатками:
Рассматривался один перекресток и не учитывались соседние;
Не изучался реальный перекресток.
Лишённой этих недостатков является только модель светофора, расположенного в центре Куала-Лумпура (Малайзия).

Цель работы
Целью нашей работы является исследование возможностей светофора с нечеткой логикой, установленного на перекрестке при различных интенсивностях движения. В качестве изучаемого перекрестка взята площадь Горская (Лыщинского).

Постановка задачи
Достижение поставленной цели заключено в решении следующих задач:
моделирование работы светофора с нечетким управлением;
сравнение эффективности работы стандартного и нечеткого светофоров.
Для решения вышеизложенных задач использовались модули системы инженерных вычислений MatLab, которые существенно упрощают процесс нечёткого логического вывода.

Математический аппарат
Е – универсальное множество,
х – элемент Е
R – некоторое свойство.
Нечеткое подмножество отличается от обычного тем, что для элементов х из Е нет однозначного ответа «да-нет» относительно свойства R.
В связи с этим нечёткое подмножество А универсального множества Е определяется как
множество упорядоченных пар
А={μА (х)/ х }.
μА (х) – характеристическая функция принадлежности,
принимающая значения в некотором упорядоченном множестве М (например, М=[0;1]).
Функция принадлежности указывает степень принадлежности элемента х подмножеству А.
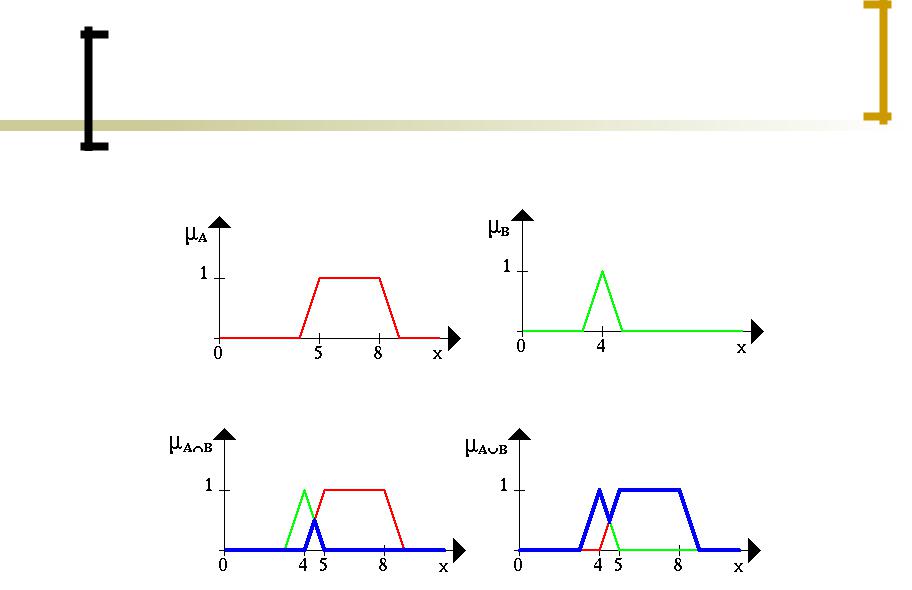
Операции с множествами
Нечеткий интервал между 5 и 8 |
Приблизительно 4 |
Пересечение множеств |
Объединение множеств |

Нечеткая переменная
Нечеткая переменная описывается набором (β, X, A), где
β – это название переменной;
X – универсальное множество (область рассуждений или область определения);
A – нечеткое множество на X, описывающая ограничения (т.е. μА (х)) на значения нечёткой переменной β.

Лингвистическая переменная 
Каждая лингвистическая переменная состоит из набора (β, T, X, G, M), где
β – название лингвистической переменной;
T – множество значений;
G – процедура образования новых термов Т;
M –процедура задания на Х нечётких подмножеств.
