Методы и модели теории графов и сетевого

моделирования.

В коммерческой деятельности большинство возникающих задач удобно представлять для восприятия и анализа в виде сетей, которые позволяют ответить на два главных вопроса: до какого места необходимо дойти (цель) и какой путь следует избрать (как). Коммерческую деятельность можно рассматривать как совокупность задач, предназначенных для распределения товаров, денег, документов, информации о поставках и покупателях воды, нефти, газа, электроэнергии, теле- и радиосистем. Наглядность и логическая обоснованность методов сетевого анализа позволяют выбрать довольно естественный подход к решению задач коммерческой деятельности. Сетевые модели для людей, не занимающихся научной работой, являются более понятными, чем сто раз услышать. В значительной степени методы сетевого анализа основаны на теории графов – области математики, началом развития которой явилась задача о кенигсбергских мостах, сформулированная швейцарским ученым Л. Эйлером в 1736г. Через реку Прегель, на которой стоял горд Кенигсберг, построено семь мостов (рис 4.1.1.), которые связывали с берегами и друг с другом два острова. Задача заключалась в том, чтобы пройти по всем мостам только один раз и вернуться обратно к началу маршрута. Эйлер доказал неразрешимость этой задачи.

Позже Д. К. Максвелл и Г. Р. Кирхгоф на основе исследования электрических цепей сформулировал некоторые принципы сетевого анализа. Были разработаны методы расчета наибольшей пропускной способности телефонных линий. В 40-х годах в результате развития теории исследования операций был разработан ряд математических методов, необходимых для анализа больших систем. В 50-60-х годах проводилась работы по построению новых сетевых моделей и разработке алгоритмов их решения на основе элементов теории графов.

Рис. 4.1.1. Модель задачи о кенигсбергских мостах.

4.1. Элементы теории графов.

В коммерческой деятельности коммерсантам постоянно приходится решать задачи поиска покупателей продукции, товаров, имеющихся в распоряжении у предприятий, клиентов-посредников как на территории России, так и за рубежом. При этом в движении постоянно преобладают люди, деньги, товары, документы, информация. После определения возможных мест, которые необходимо посетить. Возникает задача выбора оптимального маршрута их посещения, так называемая задача коммивояжера, которая представлена графически на рис. 4.1.2.

Структура изображения задачи на рис. 4.1.1. называется графом. Граф задается двумя множествами: непустым множеством X и множеством U, содержащими пары элементов из множества. При этом элементы множества U могут повторяться, а также могут повторяться элементы в парах. Граф, заданный на множествах X и U , обозначается G=(X,U) . Если элементы в парах множества U не упорядочены, то граф называется неориентированным, в противном случае – ориентированным, или орграфом.

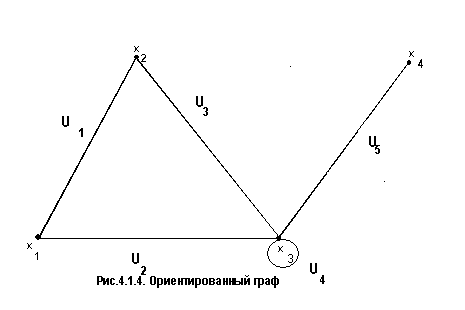
Элементы множества X называются вершинами графа, а множество U – ребрами для неориентированного графа и дугами для орграфа. На плоскости граф задается в виде точек (вершин) и линий, соединяющих некоторые из них (ребер или дуг). На рис. 4.1.3, 4.1.4 изображены соответственно неориентированный и ориентированный графы.

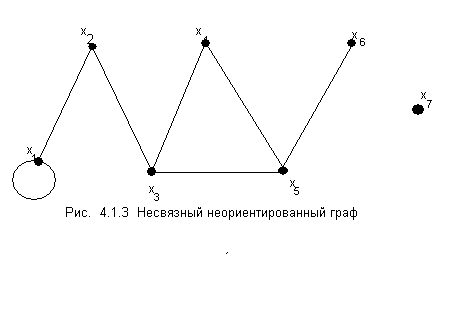
Для неориентированного графа на рис. 4.1.3 множества вершин X и ребер U можно записать так:

Х =

U=

Для ориентированного графа множества вершин и дуг записывается следующим образом:

Х = U=илиU=

Приведем ряд определений для неориентированных графов.

Ребро, начало и конец которого совпадают, называются петлей (х,х) ,рис.4.1.3.

Вершины называютсясмежными, илисоединенными, если существует ребро, их соединяющеевершиныхихнесмежные.

Если вершина является началом или концом ребра, то вершина и ребро называются инцидентными.

Степенью вершины называется число инцидентных ей ребер, степень вершины х обозначаетсяd(x) . Например, рис. 4.1.2d(х=2;d(х)= 3;d(х)= 2;d(х)= 3;

d(х)= 3, поскольку реброучитывается дважды. Вершина степень которой равна нулюd(х)= 0, называетсяизолированной х. Вершиной, степень которой равна единицеd(х)= 1, называетсявисячей, илитупиковой х.

Последовательность вершин и ребер, в которой конец предыдущего ребра совпадает с на чалом следующего, называется маршрутом.Число ребер в маршруте определяет его длину:- маршрут, длина которого равна 6, рис. 4.1.3.

Цепьюназывается маршрут, в котором всеребрапопарно различны. Например,- цепь, длина которой равна 4.Простойназывается цепь, в которой все вершины попарно различны, например,,рис.4.1.3.

Граф называется связным, если для любых двух его вершин существует цепь, соединяющая эти вершины. Граф представленный на рис. 4.1.2. – связный , а на рис. 4.1.3 – несвязный, поскольку не существует цепи, соединяющей вершинус остальными.

Расстоянием между вершинами связного графа называется длина самой короткой цепи, соединяющей вершины.

Диаметромграфа называется максимальное расстояние между его вершинами.

Циклом (простым циклом) называется цепь (простая цепь), начало и конец которой совпадают( на рис, 4.1.3. эта последовательность ()).

Цикл в графе называется эйлеровым, если он содержит все ребра графа. Связанный граф, в котором есть эйлеров цикл, называетсяэйлеровым графом. Его можно нарисовать, не отрывая карандаша от бумаги и не повторяя линий «одним росчерком» (рис. 4.1.7.б).

Подграфом графа G называется графGс множеством вершин Хи множеством реберU, такой, что ХХ, аUU.Для графа на рис. 4.1.3. подграфом может быть графG= (Х,U),где Х=, аU={.

Подграф называется собственным, если он отличен от самого графа, напримерGиG.

Компонентной связности графа называется его связный подграф, не являющийся собственным подграфом никакого другого связанного подграфа данного графа. На рис. 4.1.3 граф имеет две компоненты связности.

Вершина графа, удаление которой повышает число компонент связности, называется точкой сочленения. Подудалением вершиныпонимается удаление самой вершины и всех инцидентных ей ребер. Точкой сочленения является, например, вершинах(см. рис. 4.1.3), удаление которой приводит к появлению третьей компоненты связности.

Деревом называется связный граф без циклов рис. 4.1.5.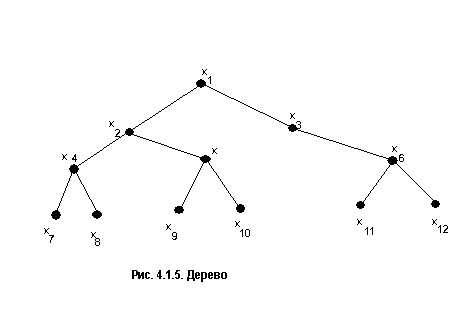

Вершина хявляетсякорнем дерева.Лесом называется граф без циклов, представляющий собой совокупность деревьев рис. 4.1.6.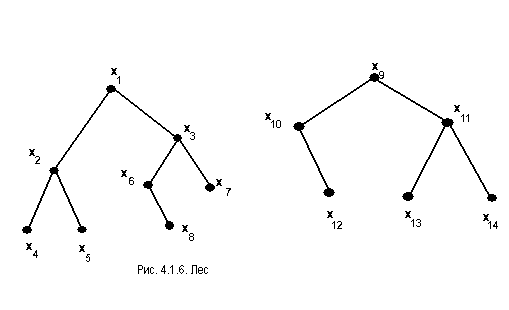

Граф называется полным, если любые две его вершины соединены ребром (см. рис. 4.1.2).

Граф называется регулярным степени d, если все его вершины имеют степень 1, называется паросочетанием. Граф называется двухдольным, если множество его вершин X может быть разделено на два непересекающихся подмножества таким образом, что каждое ребро графа соединяет вершины из двух разных подмножеств.

Гамильтоновым цепьюназывается простая цепь, содержащая все вершины графа. Например, для графа рис. 4.1.7.а цепь (6,1,5,4,3,2,8,9,10,11,12,13,14,15,20,19,18,17,16,7) является гальмитоновой.

Гальмитоновым цикломназывается гальмитоновая цепь, начало и конец которой совпадают. Если в конце предыдущей цепи дописать вершину 6, получимгальмитоновцикл.

Графназываетсягальмитоновым, если в нем имеется гамильтонов цикл (см. рис. 4.1.7а).

Термин гальмитонов связано с именем голландского математика У. Гамильтона, который в 1859 г. Предложил игру «Кругосветное путешествие». Каждой из двенадцати вершин додекаэдра (см. рис. 4.1.7а) соответствует один из городов мира. Необходимо, переезжая из города в город по ребрам додекаэдра, посетить каждый город только один раз и вернуться назад. Эта задача сводится к поиску простого цикла, проходящего через каждую вершину графа.

Задачи, касающиеся эйлеровых и гамильтоновых цепей и циклов, часто встречается а практике. Например. В ситуациях, когда качество выполнения комплекса коммерческих операций, работ, мероприятий существенно зависят от последовательности, в которой они выполняются.

Графназываетсявзвешенным, если каждому его ребру поставлено в соответветствие некоторое число, называемоевесом ребра, например расстояние между городами, стоимость или время проезда между ними.

Задача коммиваяжера можно представить как в виде ориентированного, так и неориентированного графа рис.4.1.8а,б.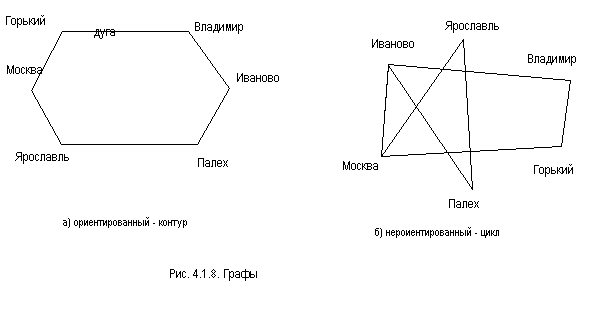

Предложенный вариант решения задачи коммиваяжера представляет собой кольцевой маршрут, где каждый город посещается только один раз, начиная с любого населенного пункта.

Для ориентированных графов в основном все определения сохраняются, однако имеются некоторые отличия. Последовательность дуг. В корой конец предыдущей дуги совпадает с началом следующей, называется путем. Длина пути определяется количеством в нем дуг. Путь называетсяпростым, если в нем дуга не встречается дважды, в противном случае он являетсясоставным. Путь, который начинается и заканчивается в одной и той же вершине, называетсяконтуром.

В ориентированном графе пользуются термином не путь, а цепь, а вместо контура –цикл.

В графе рис. 4.1.4 путем является, например, последовательность. Последовательностьпутем не является, так как не существует дуги, соединяющейхи х.

Для ориентированного графа вместо степени вершины вводится понятие полустепеней исхода и захода. Если вершина является началом дуги, то дуга называется исходящей из вершины, если концом, то -заходящей.Полустепенью исхода вершины d называется число дуг, исходящих из этой вершины,d- число дуг, заходящих в вершину. Для графа, изображенного на рис. 4.1.4, можно записать:

dddd

При выполнении анализа на компьютере граф неудобно записывать графически, а лучше представлять его в виде матриц, операции с которыми достаточно просто проводить на компьютере.

Известно несколько типов матриц. Позволяющих задавать граф.

Матрицей смежностиграфа, содержащего n-вершин, называется квадратная матрица A, каждый элемент которойaопределяется следующим образом:

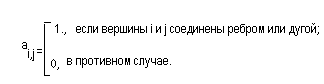
Для графа с квадратными ребрами(дугами) вместо 1 записывается число ребер (дуг) между вершинами i иj.

Для неориентированногографа, представленного на рис. 4.1.3, матрица смежности имеет размерность (7х7) и записывается в виде

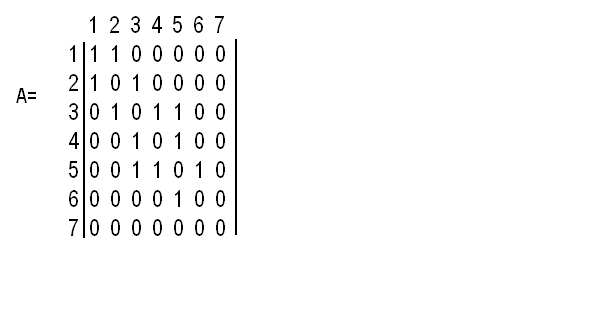
Слева и сверху проставлены номера вершин.

Для ориентированногографа. изображенного на рис. 4.1.4, матрица смежности имеет размерность (4х4) и записывается в виде

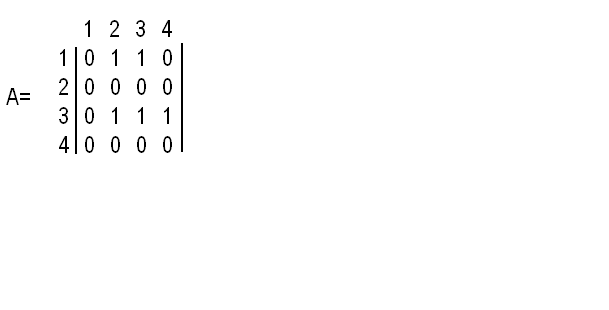
Матрицу смежности чаще применяют для задания неориентированногографа. Для заданияориентированногографа лучше использовать матрицу инцидентности.

Матрицей инцидентности ориентированногографа сn вершинами иmребрами называется матрицейВсnстроками иmстолбцами, элемент которойbопределяется следующим образом:

Для ориентированного графа, представленного на рис. 4.1.4, матрица инцидентности Вимеет следующий вид:

Взвешенный ориентированный граф без петель, в котором выделено k-вершин, называемых полюсами, является k-полюсной цепью. Среди сетей особо выделяется двухполюсная транспортная сеть (рис. 4.1.9) S=(N,U)с множеством вершинNи множеством дуг U, для которых выполняется следущее условие:

1)существует только одна вершина сети s N, в которую не заходит не одна дуга. Эта вершина называется входом, или истоком сети;

2) существует только одна вершина сети t N, из которой не выходит ни одной дуги сети. Эта вершина называется выходом, или стоком сети;

3) каждой дуги сети uU поставлено в соответствии неотрицательное числос(u), называемое пропускной способностью дуги.

Примерами вершин сети могут быть пересечения автострад, электростанции, телефонные узлы, железнодорожные узлы, аэропорты, водохранилища, товарные склады. Примерами дуг сети могут быть дороги, линии электропередачи, телефонные линии, авиалинии, водные магистрали, нефте- и газопроводы.

Постановку и решение подобных задач можно получить с помощью методов сетевого моделирования.

4.2 Природа потоков в сетях и принцип их сохранения

Сходство сетевых представлений наблюдается в природе, технике и различных сферах деятельности человека. Так, например, с высоты птичьего полета или самолета можно наблюдать сетевую модель формирования реки, например Волги от её истоков маленькие ручейки и реки, соединяясь во взаимосвязанные артерии, объединяются в одно большое русло, по которому потоки воды устремятся в Каспийское море. Такие же аналоги представляют собой сети железных дорог, по которым потоки направляются в пункты назначения, осуществляя перевозку потоков грузов и пассажиров. Совокупность линий электропередач так же представляет собой вместе энергетическую сеть, по которой потоки электроэнергии от электростанций по проводам поступают к потребителям. Автомобильные дороги как в масштабе города, района, области, так и в более крупных масштабах страны или, например, части света – Европы представляют собой сети, по которым движутся потоки автомобилей. Нефте- и газопроводы в совокупности представляют собой сети трубопроводов, по которым потоки нефти или газа поступают от источников к потребителям. Водопроводные сети обеспечивают поток воды по трубопроводам от источников к потребителям. Аналогичные сети представляют собой маршруты движения кораблей и самолетов, обеспечивающие перемещение потоков пассажиров и грузов по планете. Такие же аналоги представляют собой телефонные, радио и телекоммуникационные сети, по которым циркулируют информационные потоки, например компьютерные сети связи различного назначения. Особый интерес представляют сети, образованные движением товарных и финансовых потоков, которые могут пояснить очень многие явления нашей жизни, поскольку они являются необходимыми для обеспечения жизни людей.

Перечисленные сетевые аналоги потоковых процессов имеют динамичный характер, связанный с перемещением разных по своей природе масс в пространстве: электроэнергии, нефти, газа, воды, воздуха, железнодорожного, воздушного, автомобильного транспорта, товаров, финансов, пешеходов, информации и т.п. Причем существование этих потоков необходимо для обеспечения и поддержания жизнедеятельности человека. Именно по этому возник принцип сохранения потока. Сетевое представление взаимодействия и поведения потоков в таких сетях. Множество возникающих в таких случаях задач может быть решено с помощью теории потоков в сетях. В этой теории в качестве основы рассматриваются движения в сетях потоков любой природы от источника s к стоку t .

Определение. Потоком в сети S =(N,U) от входа sN к выходу tN называется неотрицательная функция, определённая на множестве дуг сети U, со следующими свойствами:

1. величина потока, по каждой дуге не должна превосходить её пропускной способности 0 ;

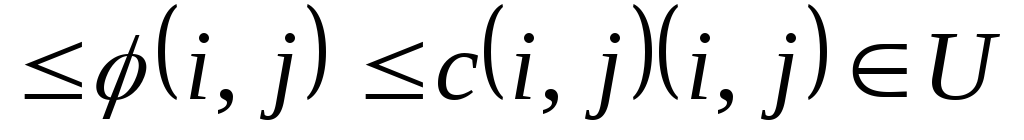2. величина потока, входящего в каждую вершину сети, за исключением входа и выхода, равна величине потока, выходящего из этой вершины.

где

- множество вершин, инцидентных дугам, направленных от вершиныi;

- множество вершин, инцидентных дугам, направленныхrвершинti.

Из определения потока следует, что величина потока не исчезает и не накапливается в вершинах сети, и, следовательно, количество потока из входа s равно количеству потока, заходящему в выход t. Это значение называется величиной потока V. Таким образом, поток в сети сохраняется, а величина потока равняется сумме значений потоков, выходящих из вершины s или входящих в вершину t:

Представленная ориентированная сеть S=(N,U) имеет множество вершин N={1,2,3,4} и множество дуг U={(1,2);(2,3);(2,4);(1,3);(3,4)}.

Количественные характеристики дуг сети, а также взаимосвязь между её узлами могут быть представлены с помощью матрицы расстояний L=или матрицы стоимостей C=.

Для ориентированной сетки рис. 4.2.1 матрица смежности имеет вид

	1	2	3	4
1	0	1	1	0
2	0	0	1	1
3	0	0	0	1
4	0	0	0	0

Матрица инцидентности ориентированной сети рис. 4.2.1 имеет вид

На рис. 4.2.1 стрелками показано направление одностороннего разрешенного движения потоков автомобилей. От одного перекрестка iдо другогоj пропускная способность по дуге по каждой улице ограничена и определяется шириной улиц и максимально допустимой скоростью движения, например 60км/ч. В связи с этим мощность автомобильного потокане может превысить допустимуюс(i,j).Таким образом выполняется первое свойство потока, условие существования статического или устойчивого потока для каждой улицы:

0

Рассматривая взаимодействие ограничений по каждой улице и в совокупности, вместе по всем перекрёсткам (вершинам сети), условие сохранения потока в этой сети записывается следующим образом:

Для источника сети при i = sнет входящих потоков, следовательно,

V=

Для стока при i = tнет выходящих потоков, следовательно,

V=

Рассмотрим пример анализа ориентированной сети S=(N,U), представленной на рис. 4.2.1, N{s,1,2,3,4,t};U={(s,3);(1,3);(2,t);(3,2);(3,4);(4,t)}.

Пропускная способность указана над каждой дугой, где рядом в скобках указано значение потока. Свойство потока в данном случае выполняется. Указанные величины не превышают пропускных способностей дуг. В каждой вершине, отличной от входа и выхода, поток сохраняется. Например, в вершину 2 заходят 4 единицы потока по дугам (1,2) и ( 3, 2) и выходят 4 единицы по дуге (2,t). Величина потока V=3+4=7.

4.3 Теорема о максимальном потоке и минимальном разрезе.

Пусть в неориентированной сети S=(N,U)от источника к стоку протекает поток, величина которого равна V. Поскольку пропускная способность каждой дугиc(i,j)является величиной конечной. То максимальная величина допустимого потока всей сети тоже ограничена. Максимальный поток сети определяется на основе одного из основных понятий теории сетей – понятие разреза. Введем понятие разреза.

Множество вершин N сети S=(N,U)можно разбить на два непересекающихся подмножестваNиN, которые соединяются между собой дугами, образующими множествоU.Причем исток s принадлежит множеству узловN, а сток t принадлежит множеству узлов.Тогда величина потока из множестваNв множество, протекающего по дугамUне может быть больше, чем можно записать таким образом:

Этот барьер для потока, отделяющий множество узлов Nот множества узлов, называетсяразрезоми обозначается (N,). Разрез представляет такое множество дугU, исключение которых отделяет вход от выхода сети, и, следовательно, отделяет множествоNотсети S=(N,U)таким образом, что существование потока в таком случае невозможно, и тогда V=0. Причем начало дуги разреза принадлежит множествуN, а конец -. Таким образом в разрез входят дуги, соединяющие вершины этих множеств.

Величина максимального потока от источника s к стоку t ограничена сверху величиной разреза С(N,), определяемой суммой пропускных способностей всех входящих в него дуг множества и, следовательно, V_<С(N,).Минимальнымразрезом сетиназывается разрез, имеющий минимальную величину.

В соответствии с теоремой о максимальном потоке и минимальном разрезе, сформулированной Фордом и Фалкерсоном, величина максимального потокаот входа s (источника) в выход t ( сток) равна величинаминимального разреза, отделяющего вход и выход сети и, следовательно,

.

Рассматриваемые сети являются сетями с ограниченной пропускной способностью, что имеет распространение в реальной жизни. Это послужило поводом к появлению и постановке задач о максимальном потоке, связанных с определением максимально допустимой величины V при соблюдении условий, записанных в виде системы уравнений и неравенств.

В сформулированной выше задаче для сохранения потока автомобилей рис. 4.2.1, например, через перекресток (3) необходимо, чтобы поступающие потоки к этой вершине (3) (1,3) и(2,3) равнялись величине потока, вытекающего из этой вершины(3,4), что можно записать

(1,3) +(2,3) =(3,4) или(1,3) +(2,3) -(3,4) = 0

Аналогичные уравнения можно записать для остальных вершин сети. Поскольку задача заключается в определении максимально возможного потока в сети, то необходимо последовательно вычислить потоки через все разрезы и выбрать из них минимальный.

Разрез АА на рис. 4.2.1 отделяет источник (1)от стока (4), в данном случае вершину (4) от остальных вершин (1,2,№). Величина разреза определяется пропускной способностью входящих в него дуг (2,3) и (3,4) и соответственно равна С(2,4)+ с(3,4) = 2+ 8 =10. затем можно определить все другие возможные варианты разрезов (В,В) и (С,С). Тогда величина максимального потока от источника к сток равна величине минимального разреза:

min

Приведенный вариант анализа фрагмента сети автомагистралей указывает на возможность применения приведенного принципа сохранения потока в коммерческой деятельности. Это позволит своевременно принимать оптимальные управленческие решения и облегчить оперативное вмешательство по регулированию не только автомобильных, но финансовых или торговых потоков.

Пример.Построим разрезы для сети, представленные на рис. 4.3.1 для различных множествN:

1) N=тогда= следовательно, разрезU=(рис.4.3.2.), таким образом, С=( N,) = 10 + 4 + 3 + 9= 26

2) N=тогда= следовательно, разрезU=

(рис.4.3.3.), таким образом, С = ( N,) = 5 +7 + 2 = 14

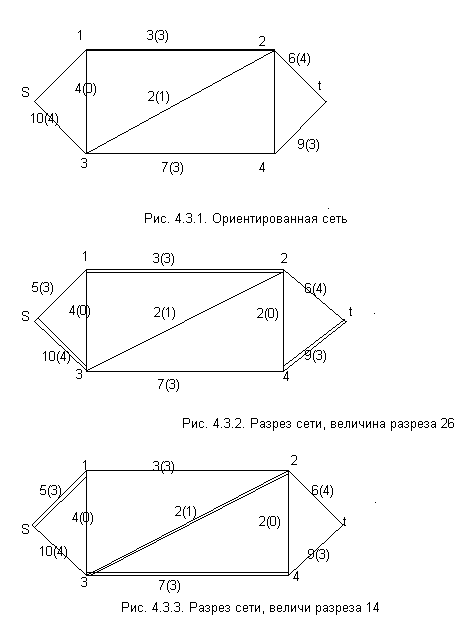
На рисунках дуги разрезов выделены. Из рисунков видно, что после удаления дуг разрезов перестают существовать пути от входа в сети s к выходу t. Разрезы имеют различную пропускные способности. Минимальным разрезом сети называются разрез, имеющий минимальную пропускную способность.

Рассмотренный алгоритм и примеры моделирования позволяют решать аналогичные по своей природе задачи по бесперебойному снабжению потоками электричества, топлива ( газа, мазута ), воды , продовольственными и непродовольственными товарами населенных пунктов и таким образом предупредить появление критических ситуаций в городах и поселках нашей страны.