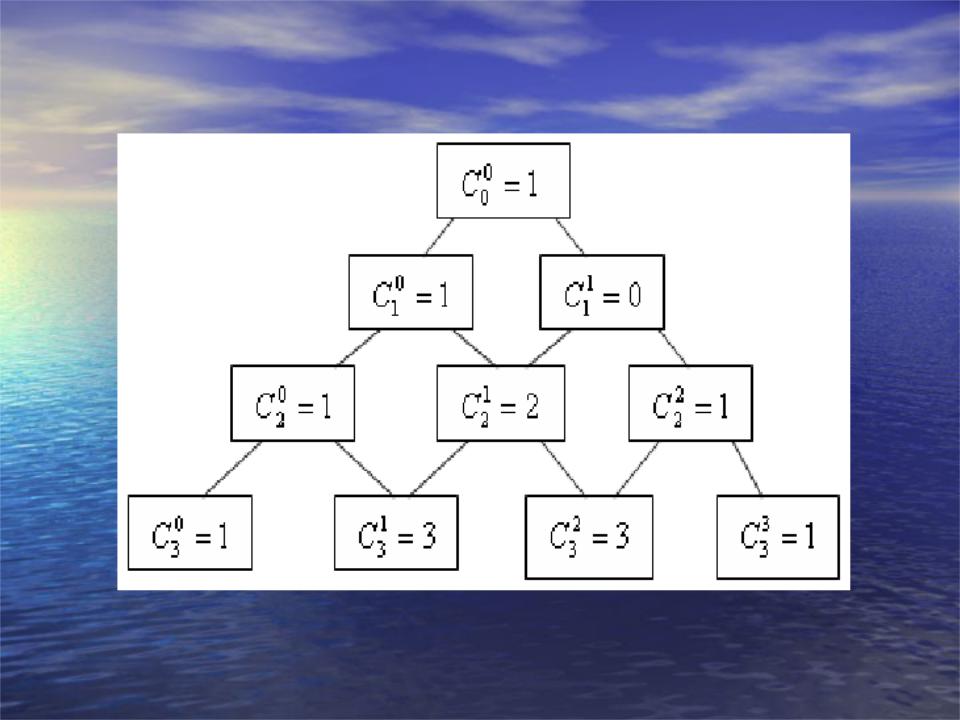
•Треугольник Паскаля:
•Свойство 3° Положим
Sn Cn0 Cn1 |
... Cnn . |
|
|
|
|
|
|
|
|
|
Так как каждое число строки с номером |
||||||||||
п входит в качестве слагаемого в два |
|
|||||||||
соседних числа следующей строки, то |
|
|||||||||
|
|
S |
|
= 2S . |
|
|
|
|||
Следовательно, S |
n+1 |
|
|
n |
|
|
|
|||
|
2S |
|
22 S |
|
... 2n 1 S |
|
2n 1, |
|||
т.к. S =1. |
|
n 1 |
|
|
n |
|
n 1 |
|
0 |
|
0 |
|
|
|
|
|
|
||||
§ 4. Бином Ньютона
2 |
2 |
|
2 |
и |
3 |
•(a + b) =a +2ab + b |
(a + |
||||
2 |
|
2 |
3 |
|
|
b) = а +3а b + 3ab +b . |
|
||||
•
(a b)n Cn0an Cn1an 1b ... Cnk an kbk ... Cnnbn.
• Доказательство. Если, не приводя подобные члены, перемножить n скобок (а + b), то
n k k
получится сумма, состоящая из слагаемых
n k k
вида a b , k=0,1,…,n. Для данного k слагаемое a b получается только в том случае, если в каких-то к скобках мы возьмем
n k k
b, a остальных (n - k) скобках - a. Следовательно, число слагаемых вида a b будет равно числу способов, которымиC k можно
n
выбрать (без учета порядка выбора) k скобок из n скобок, т.е. . Утверждение доказано.
•Если в формуле (5) взять а =b = 1, то получится известное нам свойство 3° Cnk чисел , а если взять а=1, b = -1, то получим еще одно комбинаторное равенство:0 1 2 n n
С1 Сn Cn ... ( 1) Cn 0.
(a1 a2 ... as )n |
|
|
n! |
|
|
a1k1 a2k2 |
...asks , |
||
|
|
|
|
|
|||||
n k !k |
!...k |
! |
|||||||
k k |
... k |
|
|
||||||
1 2 |
s |
1 2 |
s |
|
|
|
|
||
•Формула (6) называется
полиномиальной. Например,
|
2 |
3 |
3 |
3 |
2 |
2 |
• (а + b + с) = а + b + с + 3(а b + |
||||||
2 |
2 |
|
|
|
|
|
а + b с + с а + c b ) + 6abc. |
|
|||||
2 2
а с + b
•Пример 14. Найти n, если известно, что в разложенииn (1 + x) коэффициенты при5 х12и х равны.