
lab_mehanika_1 / Лаб.раб.№7-колеб
.docФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ФИЗИКИ
Исследование собственных колебаний струны методом резонанса
Методические указания к лабораторной работе № 7
(раздел «Механика»)
Ростов-на-Дону 2010
Составители: С.М. Максимов, А.Я. Шполянский, Н.В. Пруцакова
УДК 530.1
Исследование собственных колебаний струны методом резонанса: Метод. указания. - Ростов н/Д: Издательский центр ДГТУ, 2010. - 10 с.
Указания содержат краткую теорию по стоячим волнам и колебаниям струны и порядок выполнения лабораторной работы.
Методические указания предназначены для выполнения лабораторной работы студентами всех форм обучения в лабораторном практикуме по физике (раздел «Механика»).
Печатается по решению методической комиссии факультета «Н и КМ»
Научный редактор проф., д.т.н. В.С. Кунаков
© С.М. Максимов, А.Я. Шполянский, Н.В. Пруцакова, 2010
©
Издательский центр ДГТУ, 2010
Лабораторная работа № 7
Цели работы: получение на вертикальной струне стоячих волн, наблюдение картины распределения амплитуд и количественная проверка формулы для частот собственных колебаний струны.
Стоячие волны
Две когерентные и одинаковые по интенсивности волны, распространяющиеся навстречу друг другу, при определенных условиях могут создавать особого вида интерференционную картину, получившую название стоячих волн.
Интерференция – сложение в пространстве двух (или нескольких) волн, при котором в разных точках пространства происходит усиление или ослабление амплитуды результирующей волны. Интерференция возможна только для когерентных волн.
Когерентность – согласованное во времени и пространстве протекание колебательных или волновых процессов.
Стоячая волна представляет собой периодическое колебание с характерным пространственным распределением амплитуды – чередованием пучностей (максимумов амплитуды) и узлов (нулей амплитуды). Такая картина может возникать всякий раз, когда волна падает на хорошо отражающую преграду. Когерентность обеспечивается тем, что обе волны представляют собой раннюю и позднюю части одной и той же волны. Стоячие волны могут устанавливаться только при отсутствии затухания в среде и при полном отражении от границ.
Найдем
уравнение стоячей волны, а также
координаты ее узлов и пучностей. Пусть
стоячая волна возникла при наложении
двух встречных бегущих волн с одинаковыми
скоростями
![]() ,
циклическими
частотами
,
циклическими
частотами
![]() и
амплитудам
и
амплитудам
![]() Уравнения
волны,
распространяющейся вдоль положительного
направления оси х,
и волны, распространяющейся ей навстречу,
имеют вид:
Уравнения
волны,
распространяющейся вдоль положительного
направления оси х,
и волны, распространяющейся ей навстречу,
имеют вид:
;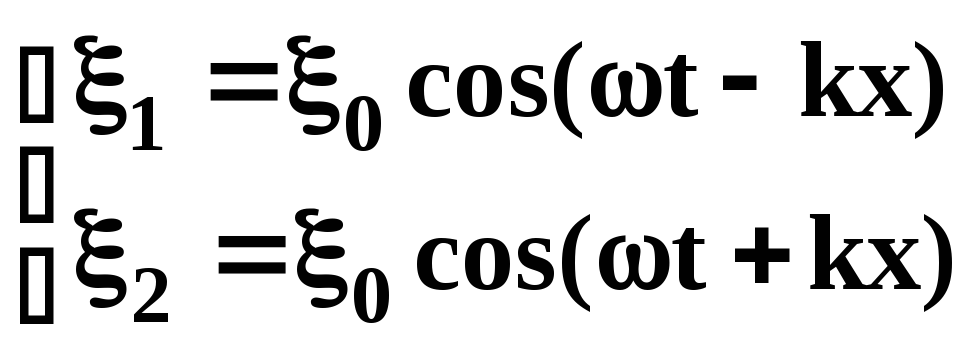
здесь
![]() и
и
![]() -
смещения точки среды с координатой х
в момент времени t,
вызванные соответственно падающей и
встречной волной.
-
смещения точки среды с координатой х
в момент времени t,
вызванные соответственно падающей и
встречной волной.
Сложив
уравнения и учитывая, что волновое число
k
связано с длиной волны
![]() :
:
![]() ,
получим уравнение стоячей волны:
,
получим уравнение стоячей волны:
![]() .
(1)
.
(1)
Из
(1) видно, что в каждой точке стоячей
волны происходят колебания с той же
частотой
![]() ,
что и у встречных волн,
но с амплитудой
,
что и у встречных волн,
но с амплитудой![]() ,
зависящей от координаты х
рассматриваемой точки.
,
зависящей от координаты х
рассматриваемой точки.
В
пучностях
амплитуда
стоячей волны максимальна и равна сумме
амплитуд складываемых колебаний
![]() ,
поэтому координаты пучностей определим
из условия:
,
поэтому координаты пучностей определим
из условия:
![]() .
(2)
.
(2)
В узлах амплитуда стоячей волны равна нулю, и координаты узлов определим из условия:
![]() (3)
(3)
То есть в стоячей волне некоторые точки среды (пучности) колеблются с максимальной амплитудой, а некоторые точки (узлы) остаются неподвижными в течение всего колебательного процесса; остальные точки среды совершают колебания с некоторыми промежуточными амплитудами.
Можно
видеть, что расстояние между соседними
пучностями, как и расстояние между
соседними узлами, равно
![]() .
Расстояние между соседними пучностью
и узлом равно
.
Расстояние между соседними пучностью
и узлом равно
![]() (рис.1).
(рис.1).
Множитель
![]() в
уравнении стоячей волны при переходе
через узел меняет знак, поэтому между
двумя соседними узлами все точки среды
колеблются синфазно, при переходе же
через узел фаза изменяется на
в
уравнении стоячей волны при переходе
через узел меняет знак, поэтому между
двумя соседними узлами все точки среды
колеблются синфазно, при переходе же
через узел фаза изменяется на
![]() ,
то есть колебания по разные стороны от
узла (в пределах полуволны) происходят
в противофазе (рис.1).
,
то есть колебания по разные стороны от
узла (в пределах полуволны) происходят
в противофазе (рис.1).
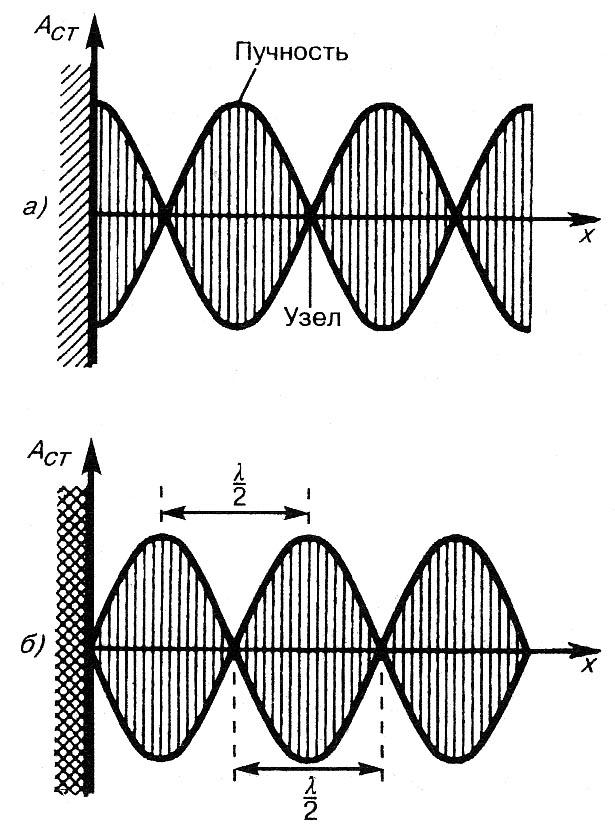
Будет ли на границе отражения узел или пучность, зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения возникает пучность (рис.1,а), если более плотная – узел (рис.1,б).
Отражаясь от более плотной среды, волна меняет свою фазу на противоположную и результат сложения этих колебаний дает узел (пример: в месте закрепления колеблющейся веревки получается узел). Этот факт принято называть «потерей полуволны».
![]()
![]()
![]()
![]()
Рис.
1. График стоячей волны. На рисунке:
![]() –
амплитуда стоячей волны,
–
амплитуда стоячей волны,
![]() -
длина волны, х
–
направление распространения.
-
длина волны, х
–
направление распространения.
Отражаясь от менее плотной среды, волна не меняет фазы в месте отражения, поэтому потери полуволны не происходит; фазы падающей и отраженной волн одинаковы. В этом случае в результате сложения колебаний одинаковых фаз получается пучность (пример: свободный конец колеблющейся веревки образует пучность).
Как известно, бегущая волна в направлении ее движения переносит энергию колебательного движения. Стоячая волна энергию не переносит, поскольку падающая и отраженная волны, имея одинаковые амплитуды, несут одинаковую энергию, но в противоположных направлениях. Поэтому полная энергия результирующей стоячей волны, заключенной между узловыми точками, с течением времени остается неизменной. Только в пределах расстояний, равных половине длины волны, происходят взаимные превращения кинетической энергии в потенциальную и наоборот.
Колебания струны
В
натянутой струне, закрепленной с обоих
концов, при возбуждении произвольного
поперечного возмущения может возникать
стоячая волна. При этом на закрепленных
концах струны должны выполняться
определенные граничные условия: концы
струны должны быть узлами стоячей волны.
Это означает, что на длине струны
![]() укладывается целое число
укладывается целое число
![]() полуволн (рис. 2). Отсюда вытекает условие:
полуволн (рис. 2). Отсюда вытекает условие:
(4)![]() или
или
![]()
Этим длинам волн соответствуют частоты
(5)![]()
где
![]() -
фазовая
скорость распространения бегущей
волны в струне, которая может быть
вычислена как
-
фазовая
скорость распространения бегущей
волны в струне, которая может быть
вычислена как
![]() .
(6)
.
(6)
Здесь
![]() -
сила натяжения струны;
-
сила натяжения струны;
![]() -
линейная плотность струны, то есть масса
единицы длины струны, вычисляется
через
объемную
плотность
струны
-
линейная плотность струны, то есть масса
единицы длины струны, вычисляется
через
объемную
плотность
струны
![]() по
формуле:
по
формуле:![]() ;
;
![]() -
площадь
поперечного сечения струны. Таким
образом, фазовая скорость бегущей волны
вычисляется по формуле
-
площадь
поперечного сечения струны. Таким
образом, фазовая скорость бегущей волны
вычисляется по формуле
![]() (7)
(7)
и выражение для частоты стоячей волны приобретает вид
![]() .
(8)
.
(8)
Частоты
![]() называются собственными
частотами
струны,
а
соответствующие им гармонические
колебания – собственными
колебаниями,
или гармониками.
Частота
называются собственными
частотами
струны,
а
соответствующие им гармонические
колебания – собственными
колебаниями,
или гармониками.
Частота
![]() называется
основной
частотой,
а остальные частоты
называется
основной
частотой,
а остальные частоты
![]() –
обертонами.
–
обертонами.
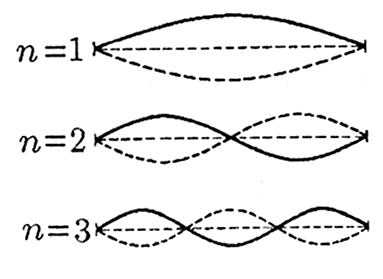
Рис.
2. Распределение амплитуд отдельных
точек струны при собственных колебаниях
струны для различных значений
![]() .
.
В общем случае колебания струны представляют собой суперпозицию (наложение) различных гармоник. В струне можно возбудить колебания, соответствующие одной из собственных частот. В этом случае мы будем иметь условие резонанса струны.
Приборы и принадлежности: вертикальная стойка со струной, электромагнитный вибратор, источник напряжения, разновесы.
В работе исследуются колебания натянутой медной струны (гибкой однородной нити). Схема экспериментальной установки представлена на рис. 3. Внешнее периодическое воздействие на струну 1 осуществляется в верхней ее точке, где конец струны прикреплен к якорю электромагнитного вибратора 2. Электромагнитный вибратор питается от сети переменным током частотой 50 Гц. К нижнему концу струны прикреплена чашка весов 4, а сама струна пропущена через отверстие малого диаметра в пластинке 3, которая может перемещаться вверх-вниз вдоль стойки.
Если нагрузить чашку весов гирьками и включить в сеть электромагнитный вибратор, то якорь электромагнита начнет совершать колебания с частотой тока сети, и по струне будут распространяться поперечные волны, которые, отражаясь от пластинки 3, образуют встречные волны. При наложении прямой и обратной волны образуются стоячие волны, если выполняется условие:
![]()
Подбирая длину струны и степень ее натяжения, можно наблюдать образование стоячей волны в струне. Длину струны с установившейся стоячей волной изменяют перемещением вверх-вниз пластинки 3. Силу натяжения F струны изменяют, меняя гирьки в чашке весов 4 (рис. 3).

Рис. 3. Схема экспериментальной установки: 1 – струна, 2 – электро-магнитный вибратор, 3 – отражающая пластина, 4 - чашка весов.
Как
видно из рисунка 3, в данной работе сила
натяжения струны равна силе тяжести,
действующей на чашку весов с грузом.
То
есть в формуле (8)
![]() ,
где
,
где
![]() - масса чашки грузом;
- масса чашки грузом;
![]() ,
,
![]() -
масса чашки,
-
масса чашки,
![]() -
масса
груза.
-
масса
груза.
Таким образом, окончательно расчетная формула для частоты стоячей волны приобретает вид
![]() .
(9)
.
(9)
Измерения
-
Включить питание электромагнитного вибратора.
-
Нагрузить струну (
 )
и, изменяя длину струны, добиться
устойчивых стоячих волн.
)
и, изменяя длину струны, добиться
устойчивых стоячих волн. -
Изменяя длину струны, измерить координаты первого, второго и третьего узлов стоячей волны -
 ,
,
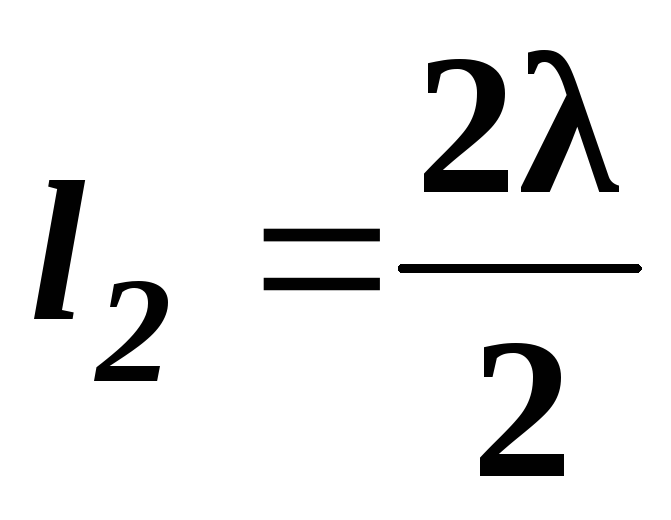 и
и
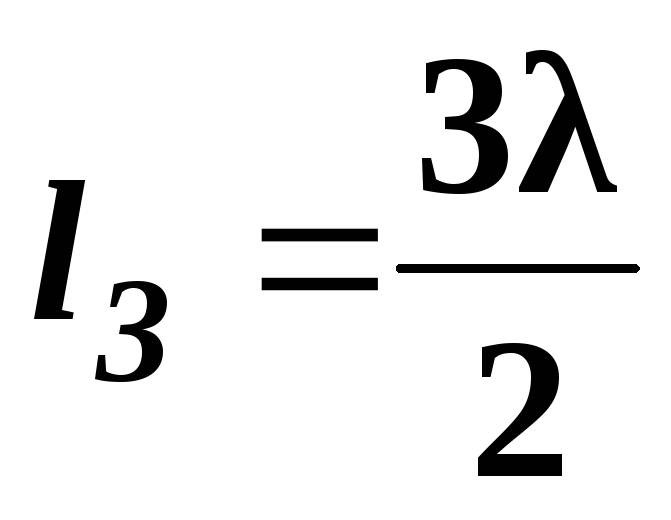 .
.
-
Повторить эти измерения для четырех других значений
 ,
увеличивая
,
увеличивая
 через 50 г.
через 50 г.
-
Для каждой серии опытов по формуле (4) найти длины волн
 ,
а также среднюю длину волны
,
а также среднюю длину волны
 ,
ее
среднюю абсолютную погрешность
,
ее
среднюю абсолютную погрешность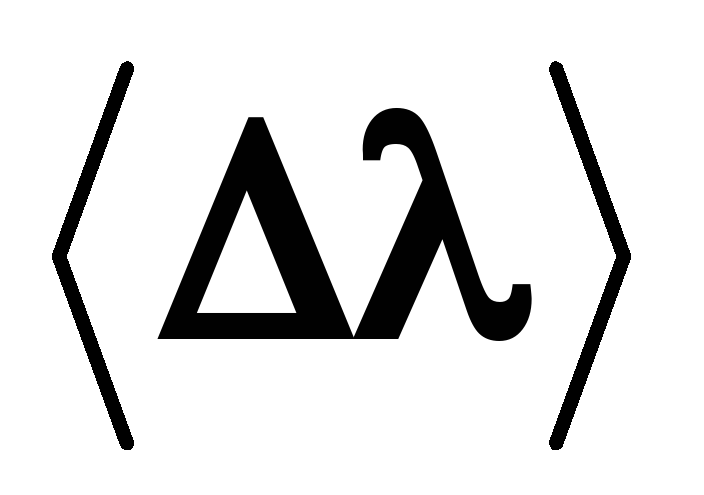 и
относительную
погрешность
и
относительную
погрешность
 ,
где
,
где
![]() . (10)
. (10)
-
Для каждой серии опытов, используя среднее значение длины волны
 ,
определить
частоту колебаний
,
определить
частоту колебаний
 по формуле (9).
по формуле (9). -
По формулам (11) и (12) для каждой из этих частот вычислить относительные и абсолютные погрешности:
![]() (11)
(11)
![]() . (12)
. (12)
|
№ |
|
|
m |
l1 |
λ1 |
l2 |
λ2 |
l3 |
λ3 |
|
|
|
|
|
|
ν |
|
Δν |
|
- |
м2 |
|
кг |
м |
м |
м |
м |
м |
м |
м |
м |
м |
м |
м |
% |
с-1 |
% |
с-1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*
Значения
S
и
![]() указаны на установке.
указаны на установке.
Контрольные вопросы
-
Что такое интерференция волн?
-
Как возникают стоячие волны?
-
Какие точки стоячей волны называют узлами? Пучностями?
-
Каковы координаты узлов и пучностей стоячей волны?
-
Переносят ли стоячие волны энергию?
-
По какой формуле находят собственные частоты колебаний струны?
-
Как получить условие резонанса струны?
Рекомендуемая литература
-
Трофимова Т.И. Курс физики. - М.: Высш. школа, 2001.
-
Савельев И.В. Курс общей физики. Электричество и магнетизм. Волны. Оптика. – СПб.: Лань, 2006.
-
Детлаф А.А., Яворский Б.М. Курс физики. - М.: Академия, 2008.
