4.2.2 Контрольный пример №2

Дана функция :

С начальным условием:

Разностная смешанная производная

Рис 5.1. Таблица приближенных значений правой разностной смешанной производной.

Рис 5.2. Таблица приближенных значений левой разностной смешанной производной.

Рис 5.3. Таблица приближенных значений центральной разностной смешанной производной.

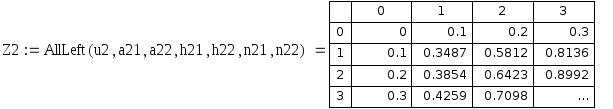
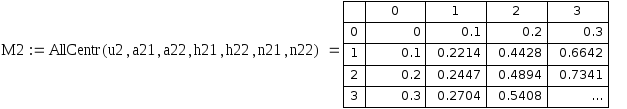
Рис 5.4 Точная смешанная производная

Рис 5.3. Таблица точных значений смешанной производной.

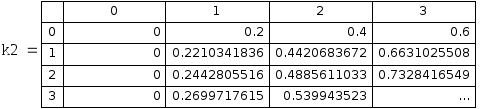
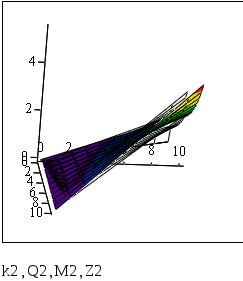
Рис. 5.4. График для сравнения точных и приближенных значений смешанной производной.

Рис. 5.5. Относительная погрешность приближенных значений правой смешанной производной

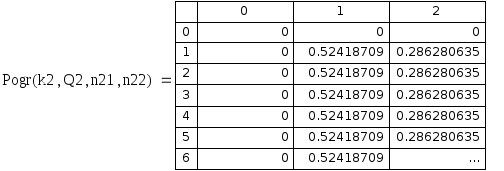
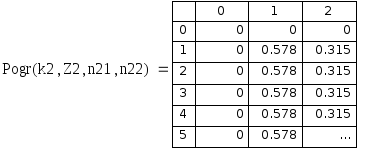
Рис. 5.6. Относительная погрешность приближенных значений левой смешанной производной

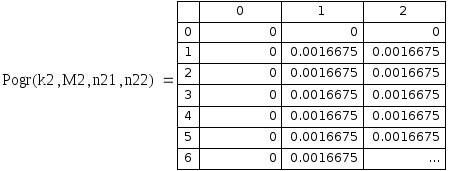
Рис. 5.7. Относительная погрешность приближенных значений центральной смешанной производной

Разностная частная производная по x

Рис 6.1. Таблица приближенных значений правой разностной частной производной по x 1 порядка.

Рис 6.2. Таблица приближенных значений левой разностной частной производной по x 1 порядка.

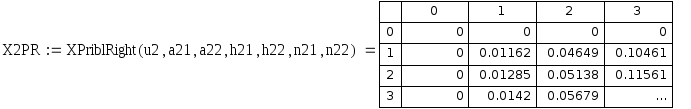
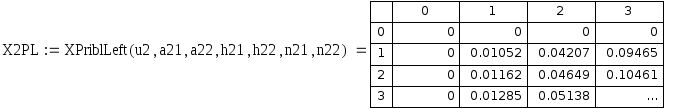
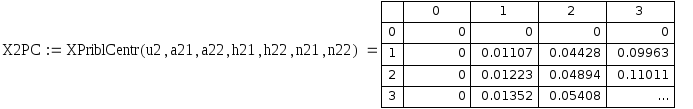
Рис 6.3. Таблица приближенных значений центральной разностной частной производной по x 1 порядка.

Рис 6.4. Таблица приближенных значений разностной частной производной по x 2 порядка.

Рис 6.5 Точная частная производная по x 1 порядка.

Рис 6.6 Точная частная производная по x 2 порядка.

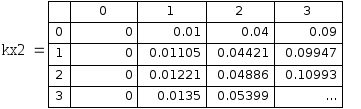
Рис 6.7. Таблица точных значений частной производной по x 1 порядка.

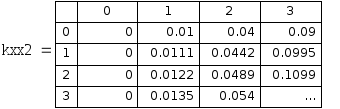
Рис 6.8. Таблица точных значений частной производной по x 2 порядка.

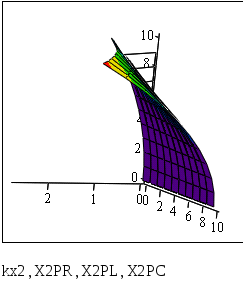
Рис. 6.9. График для сравнения точных и приближенных значений частной производной по x 1 порядка.

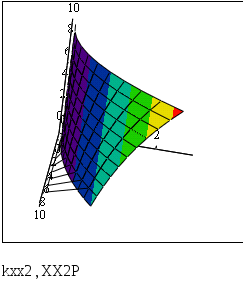
Рис. 6.10. График для сравнения точных и приближенных значений частной производной по x 2 порядка.

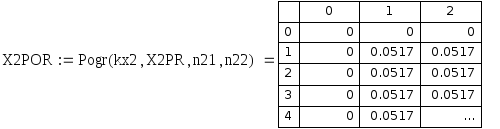
Рис. 6.11. Относительная погрешность приближенных значений правой частной производной по x 1 порядка.

Рис. 6.12. Относительная погрешность приближенных значений левой частной производной по x 1 порядка.

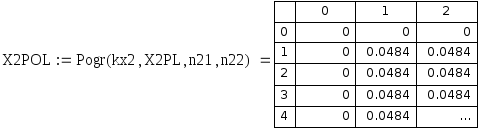
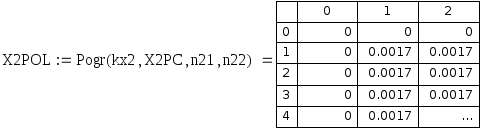
Рис. 6.13. Относительная погрешность приближенных значений центральной частной производной по x 1 порядка

Рис. 6.14. Относительная погрешность приближенных значений частной производной по x 2 порядка

Разностная частная производная по y

Рис 7.1. Таблица приближенных значений правой разностной частной производной по y 1 порядка.

Рис 7.2. Таблица приближенных значений левой разностной частной производной по y 1 порядка.

Рис 7.3. Таблица приближенных значений центральной разностной частной производной по y 1 порядка.

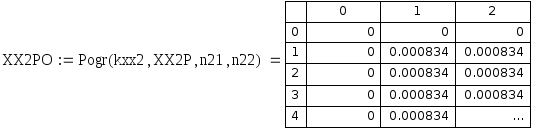
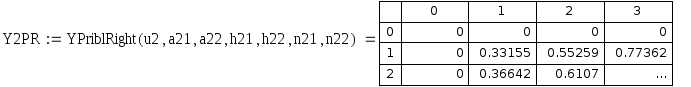
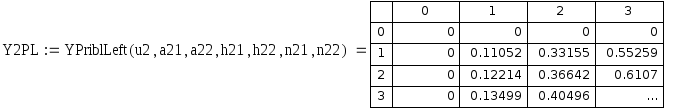
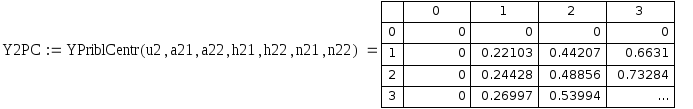
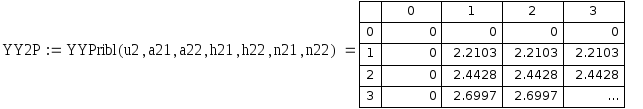
Рис 7.4. Таблица приближенных значений разностной частной производной по y 2 порядка.

Рис 7.5 Точная частная производная по y 1 порядка.

Рис 7.6 Точная частная производная по y 2 порядка

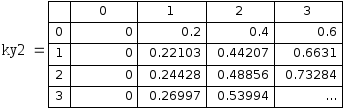
Рис 7.7. Таблица точных значений частной производной по y 1 порядка.

Рис 7.8. Таблица точных значений частной производной по y2 порядка.

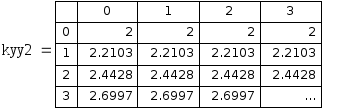
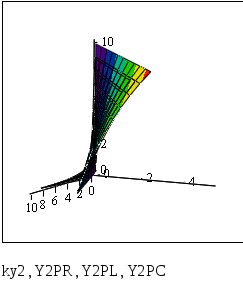
Рис. 7.9. График для сравнения точных и приближенных значений частной производной по y 1 порядка.

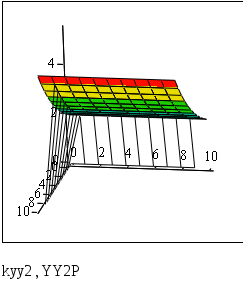
Рис. 7.10. График для сравнения точных и приближенных значений частной производной по y 2 порядка.

Рис. 7.11. Относительная погрешность приближенных значений правой частной производной по y 1 порядка.

Рис. 7.12. Относительная погрешность приближенных значений левой частной производной по y 1 порядка.

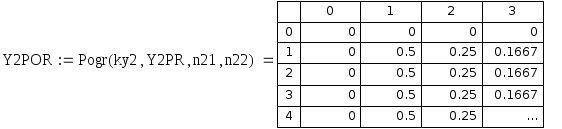
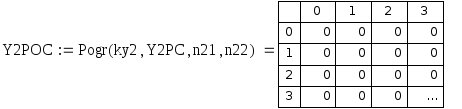
Рис. 7.13. Относительная погрешность приближенных значений центральной частной производной по y 1 порядка.

Рис. 7.14. Относительная погрешность приближенных значений частной производной по y 2 порядка.

ЗАКЛЮЧЕНИЕ

Если аналитически не удается найти частную производную, то тогда можно воспользоваться разностными формулами. Значения разностных формул для частных производных, близки к точным значениям производной. Поэтому также, очень удобно пользоваться ими при громоздкости выкладок.

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1. Б.В.Соболь, Б.Ч.Месхи, И.М.Пешхоев. Практикум по вычислительной математике. - Ростов-на-Дону: Феникс, 2008;

2. Б.П.Демидович, И.А.Марон. Основы вычислительной математики. - СПб.: Лань, 2007.

3. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Бином, 2004.

4. Cайт википедия [Электронный ресурс]. – Режим доступа: ru.wikipedia.org/wiki/Частные_уравнений.

5. Cайт википедия [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Mathcad;