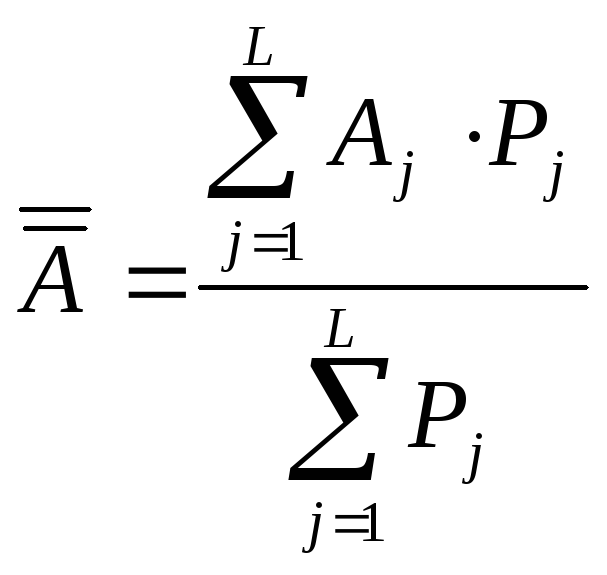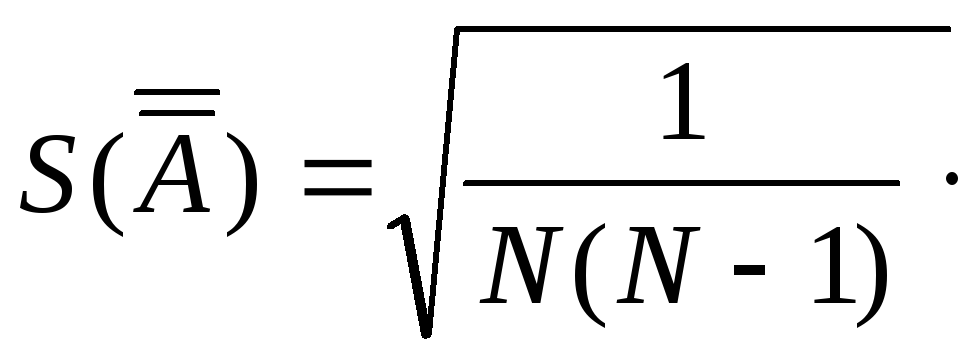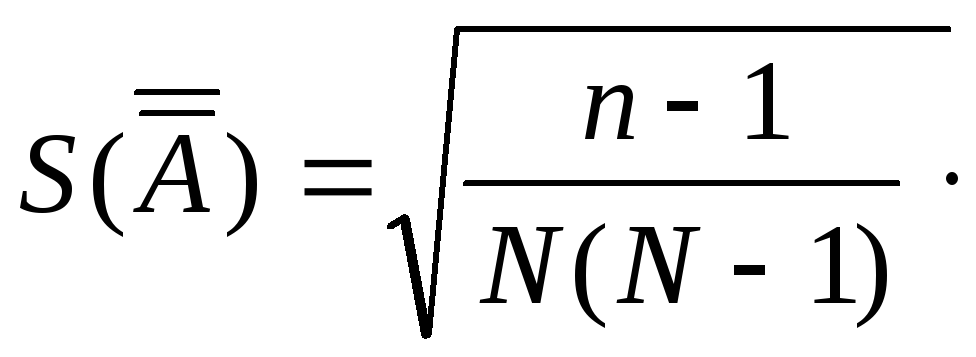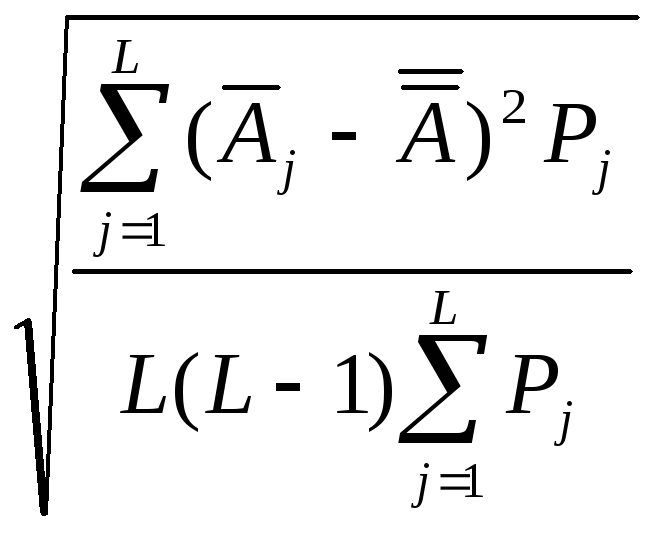9 Группы результатов измерений
9.1 Основные положения
При проведении измерений параметра, особенно в течение длительного времени, меняются условия измерений, часто возникает необходимость в смене операторов, замене средств измерений. Это приводит к разной точности результатов измерений. На точность результатов будет также влиять число измерений.
Для получения единого результата таких групп измерений необходимо чтобы:
- границы не исключенных систематических погрешностей в группах результатов измерений были одинаковы;
- группы результатов измерений были однородны.
Порядок систематической обработки однородных групп результатов измерений зависит от их равноточности. Если группы равноточны, то они обрабатываются как единая совокупность результатов измерений, как показано в главе 8. Если группы неравноточны, то для каждой из них вводится дополнительная характеристика – статистический вес, с учётом которого проводится дальнейшая обработка результатов измерений. Проверку однородности и равноточности групп можно выполнить по критериям, представленным в таблице 9.1.
Таблица 9.1 – Критерии для проверки групп результатов измерений
|
Распределение дан- ных в груп- пах Число групп |
По нормальному закону |
По закону, отличному от нормального | |||
|
2 |
≥3 |
2 |
≥3 | ||
|
П Р О В Е Р К А |
однородности |
Стьюдента |
Фишера |
Уилкоксона |
² |
|
равноточности |
Фишера |
Бартлетта |
Сиджела-Тьюки |
Сиджела-Тьюки (группы попарно) | |
Рассмотрим порядок проверки групп с помощью перечисленных критериев.
Критерий Стьюдента
оценивает допустимость различия средних
арифметических значений Ā![]() и Ā
и Ā![]() вгруппах.
Это различие считается допустимым, если
выполняется неравенство:
вгруппах.
Это различие считается допустимым, если
выполняется неравенство:
![]()
![]()
![]() ≤t
≤t![]() (9.1)
(9.1)
где S![]() ,
S
,
S![]() – дисперсии в группах;
– дисперсии в группах;
n![]() ,
n
,
n![]() – объёмы групп;
– объёмы групп;
t![]() – коэффициент Стьюдента (приложение
А) для заданной доверительной вероятности
Р и числа степеней свободы f=n
– коэффициент Стьюдента (приложение
А) для заданной доверительной вероятности
Р и числа степеней свободы f=n![]() +n
+n![]() -2.
-2.
Критерий Фишера оценивает допустимость расхождения дисперсий групп.
Две группы считаются равноточными, если выполняется неравенство:
![]()
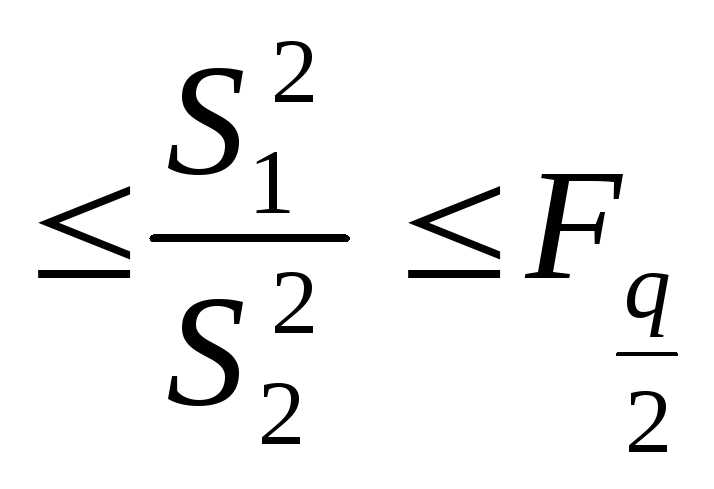 ,
(9.2)
,
(9.2)
где F![]() - значение критерия Фишера (приложение
К) для уровня значимости
- значение критерия Фишера (приложение
К) для уровня значимости
![]() и числа степенной свободы
и числа степенной свободы![]() =n
=n![]() -1,
-1,
![]()
![]() =n
=n![]() -1.
-1.
Для оценки однородности нескольких (более двух) групп рассчитывают:
- межгрупповую дисперсию:
![]() S
S![]() =
=![]() ,
(9.3)
,
(9.3)
где L – число групп;
n![]() – объём j-той
группы;
– объём j-той
группы;
![]() –среднее
арифметическое значение результатов
измерений в j-той
группе;
–среднее
арифметическое значение результатов
измерений в j-той
группе;
![]() –среднее
арифметическое значение по всем группам:
–среднее
арифметическое значение по всем группам:
![]() ,
(9.4)
,
(9.4)
где N – общее число результатов измерений:
![]() ;
(9.5)
;
(9.5)
- внутригрупповую дисперсию:
![]() (9.6)
(9.6)
Группы считаются однородными, если выполняется неравенство:
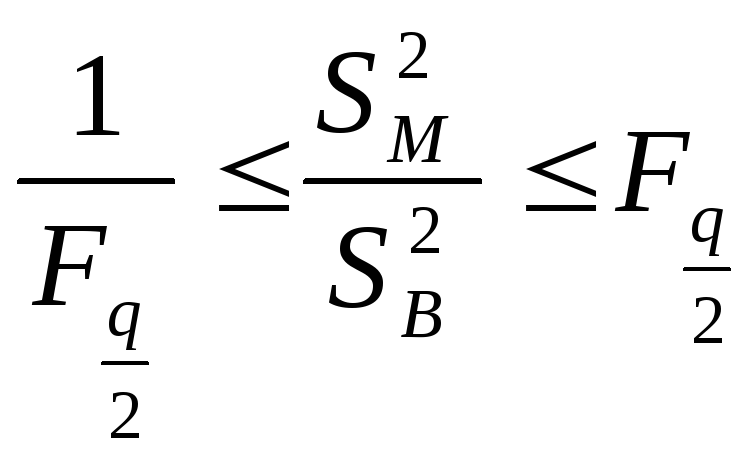 ,
(9.7)
,
(9.7)
где
![]() - значение критерия Фишера для уровня
значимости
- значение критерия Фишера для уровня
значимости![]() и числа степенней свободы
и числа степенней свободы![]() и
и![]() .
.
Критерий Бартлетта оценивает равноточность групп по соотношениям внутригрупповой дисперсии с дисперсией в группах, которые определяют значение 2:
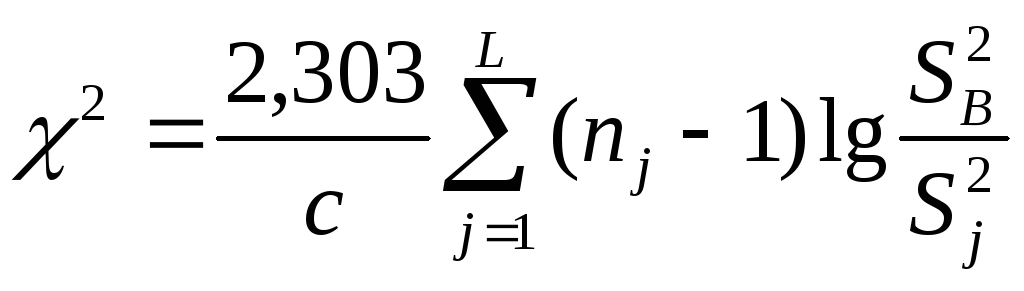 , (9.8)
, (9.8)
где 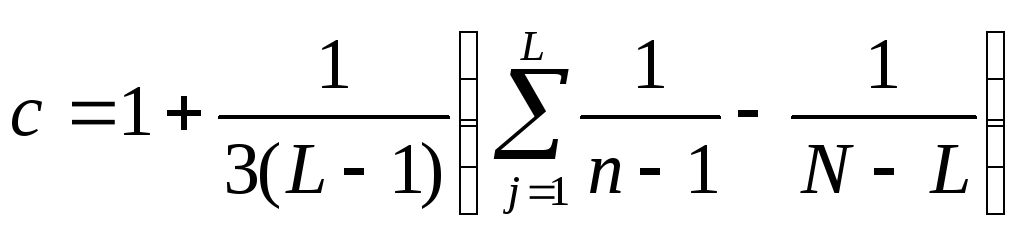 ,
(9.9)
,
(9.9)
с=1, если во всех
группах
![]() .
.
Группы становятся
равноточными, если
![]() ,
где
,
где![]() - табличное значение2
(приложение Е) для уровня значимости q
и числа степеней свободы f=L-1.
- табличное значение2
(приложение Е) для уровня значимости q
и числа степеней свободы f=L-1.
Для групп, в которых результаты измерений не подчиняются нормальному закону, применяются непараметрические (ранговые) критерии.
Критерий Уилкоксона оценивает расхождение средних арифметических значений групп по суммарному рангу результатов измерений в группе меньшего объёма:
![]() ,
(9.10)
,
(9.10)
где
![]() – ранги (порядковые номера) результатов
измерений группы меньшего объёма в
вариационном ряду, включающем результаты
измерений обеих групп.
– ранги (порядковые номера) результатов
измерений группы меньшего объёма в
вариационном ряду, включающем результаты
измерений обеих групп.
Группы считаются однородными, если выполняется неравенство:
![]() ,
(9.11)
,
(9.11)
где ![]() ;
(9.12)
;
(9.12)
![]() ,
(9.13)
,
(9.13)
где n – объём меньшей группы;
m – объём большей группы;
![]() –квантиль функции
Лапласа для значения функции
–квантиль функции
Лапласа для значения функции
![]() ;
;
Р – доверительная вероятность.
Для групп малых объемов (n+m30) значения Т табулированы (приложение М).
Критерий Сиджела-Тьюки проверяет допустимость различия рассеяния результатов по группам по условию: если выполняется неравенство (9.11), то группы считаются равноточными. Предельные значения определяются по формулам (9.12) и (9.13). Для подсчёта Т по формуле (9.10) ранги в вариационном ряду присваиваются в следующем порядке: 1- наименьшему значению , 2 - наибольшему, 3 - предыдущему перед наибольшим значением,
4 - второму после наименьшего значения, 5 - третьему после наименьшего значения, 6 - третьему перед наибольшим значением и т. п.
Критерий
![]() предусматривает группирование
экспериментальных данных по одной и
той же системе. Например, системе изr
интервалов, как показано в таблице 9.2.
предусматривает группирование
экспериментальных данных по одной и
той же системе. Например, системе изr
интервалов, как показано в таблице 9.2.
Таблица 9.2 – Схема
упорядочения данных для критерия ![]()
|
Интервалы |
Группа данных |
Сумма по строкам |
|
1,…………….,j,…………….,L | ||
|
1 . . . i . . . r |
n . . .
n . . .
|
|
|
Объёмы групп |
|
|
![]() –общее число
данных, попавших в i-тый
интервал.
–общее число
данных, попавших в i-тый
интервал.
Интервалы группировки принимают одинаковыми (кроме крайних). Число интервалов рекомендуется принимать равным: r = 8…12 при N = 100…2000, r = 10…15 при N = 200…500.
Рассчитывают ![]() по формуле:
по формуле:
![]()
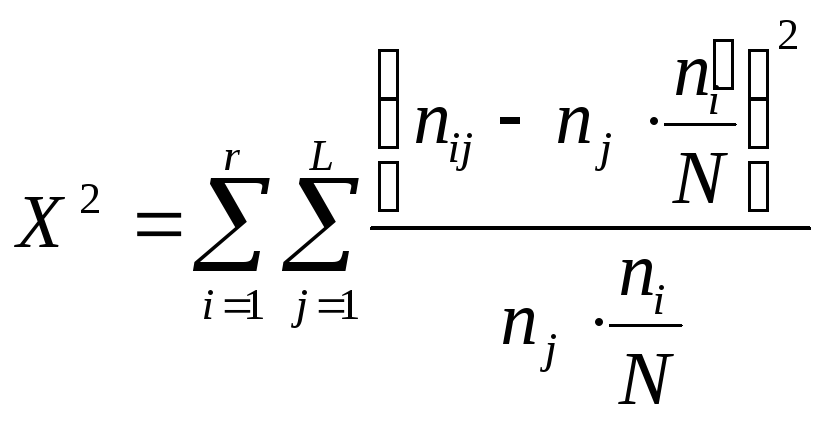 .
(9.14)
.
(9.14)
Группы считаются
однородными, если![]() ,
гдеq2
- табличное значение
,
гдеq2
- табличное значение ![]() (приложение Е) для уровня значимостиq
и числа степенней свободы:
(приложение Е) для уровня значимостиq
и числа степенней свободы:
![]() .
(9.15)
.
(9.15)
Порядок статистической обработки однородных групп результатов измерений представлен в таблице 9.3.
Таблица 9.3 – Определение результата групп измерений
|
Группы Ха- ракте- ристики |
Равноточные |
Неравноточные | |||
|
Разных объёмов |
Одинаковых объёмов | ||||
|
Для каждой группы |
Среднее арифметическое |
| |||
|
СКО |
| ||||
|
Статистичес-кий вес |
– |
| |||
|
Общие по группам |
Среднее арифметическое |
|
|
(9.21.) | |
|
СКО среднего арифметического |
(9.22.) |
|
= (9.24.) | ||
|
Число степеней
свободы для коэффициента Стьюдента
|
|
(9.27.) | |||
|
Доверительный интервал |
| ||||
*n![]() – объём наименьшей группы.
– объём наименьшей группы.

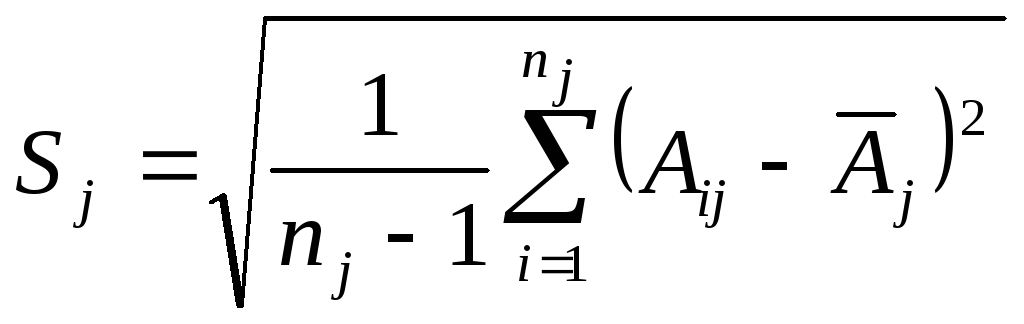 (9.17.)
(9.17.)