7. Контрольные вопросы

1. От чего зависит температура кипения воды?

2. Какая существует зависимость между абсолютным давлением и температурой кипения воды?

3. 3 Какая существует зависимость между вакууметрическим давлением и температурой кипения воды?

Лабораторная работа 2

ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ПАРАМЕТРОВ

ВЛАЖНОГО ВОЗДУХА

Цель работы – определить на основании опытов основные параметры влажного воздуха: относительную и абсолютную влажность; влагосодержание; энтальпию; психрометрическую разность; которые являются необходимыми при тепловых расчетах и конструировании ряда установок, например, сушильных.

1.Основные сведения о влажном воздухе

1.1. Влажный воздух представляет собой механическую смесь сухого воздуха и паров воды. Вследствие малых парциальных давлений пары воды считают идеальным газом. Следовательно, в условиях термодинамического равновесия (когда температура смеси сухого воздуха и паров воды, т.е. влажного воздуха одинакова по всему объёму) процессы с влажным воздухом рассчитывают по уравнениям состояния идеальных газов Клапейрона – Менделеева для смеси:

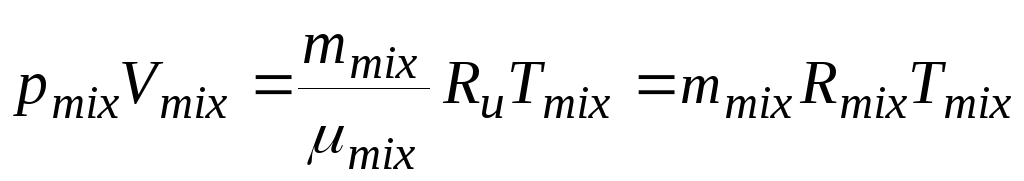, (2.1)

где р_mix –абсолютное давление смеси, Па (индекс «mix» везде относится к параметрам газовой смеси, образован от англ. mixture-смесь); V_mix – полный объём смеси, м³; m_mix – масса смеси, равная сумме масс всех компонентов:

, кг, (2.2)

где m_i – масса i-го компонента, кг; n – число компонентов в смеси;

μ_mix – кажущаяся молярная масса смеси:

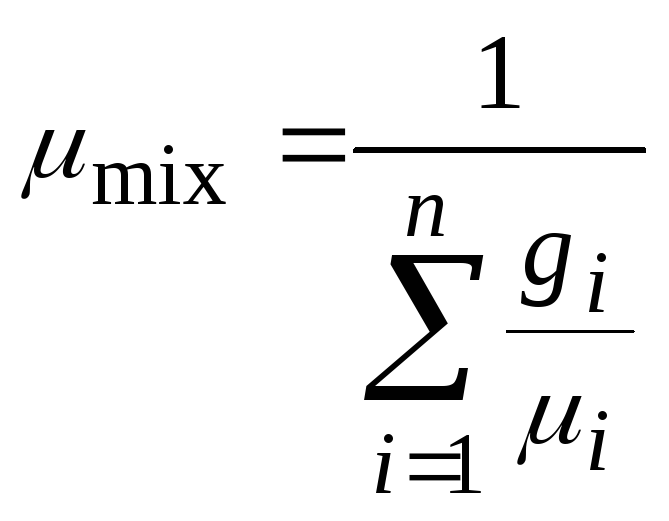, (2.3)

где g_i – массовая доля i-го компонента;

; (2.4)

R_u –универсальная газовая постоянная, R_u = 8314 Дж/(кмоль К); Т_mix – абсолютная температура смеси, К; R_mix – газовая постоянная смеси, R_mix= R_u /μ_mix.

Согласно закону Дальтона каждый газ, входящий в смесь, находится под своим парциальным давлением р_i, а сумма парциальных давлений компонентов равна давлению смеси р_mix:

. (2.5)

Следовательно, давление влажного воздуха есть сумма парциальных давлений сухого воздухаи паров воды:

. (2.6)

Поскольку модель идеального газа пренебрегает размерами микрочастиц, объём V_i, занимаемый каждым компонентом, равен объёму всей смеси V_mix:

V_i=V_mix . (2.7)

Тогда, учитывая, что отношение массы вещества к объёму есть его плотность ρ (ρ=m/V), из (2.1) для компонентов влажного воздуха запишем::

а) уравнение состояния сухого воздуха

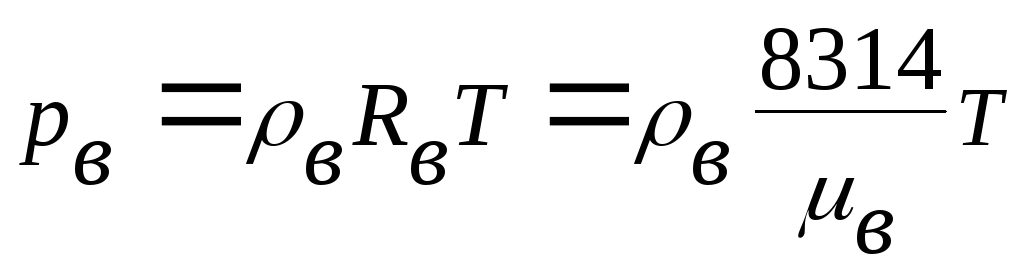; (2.8)

б) уравнение состояния паров воды

. (2.9)

Здесь

, ,,,

где ρ_п, ρ_в, ρ – плотности соответственно паров воды (абсолютная влажность), сухого воздуха и влажного воздуха (смеси); ,- молярные массы компонентов – воды, воздуха;,,- масса паров воды, сухого воздуха, влажного воздуха (смеси);V - объем влажного воздуха.

Парциальное давление паров воды является важной характеристикой влажного воздуха, так как состояние влажного воздуха определяется соотношением парциального давления паров воды p_п и давлением насыщенных паров воды р_s при температуре влажного воздуха.

Состояние насыщения (кипения жидкости) наступает, если при данной температуре давление насыщенных паров р_s равно давлению окружающей среды p. В неограниченном объеме , в замкнутом объеме.

1.2. Состояния влажного воздуха. В зависимости от соотношения р_п и р_s, можно рассмотреть следующие состояния влажного воздуха.

Ненасыщенный влажный воздух. Парциальное давление паров воды р_п меньше давления насыщения р_s при данной температуре, р_п<р_s. Температура паров воды (влажного воздуха) больше температуры насыщения (кипения) воды при данном давлении, t_в>t_s. Пары воды находятся в перегретом состоянии относительно температуры насыщения.

Насыщенный влажный воздух. Парциальное давление паров воды равно давлению насыщения при температуре воздуха, р_п=р_s. Температура влажного воздуха равна температуре насыщения воды при данном давлении, t_в=t_s.

Перенасыщенный влажный воздух. Парциальное давление паров воды больше давления насыщения при температуре воздуха, р_п>р_s. Температура влажного воздуха меньше температуры насыщения воды при давлении р_п, t_в<t_s. Происходит конденсация части паров или пары (при отсутствии центров конденсации) остаются в термодинамически неустойчивом (пересыщенном) состоянии.

1.3. Основные характеристики влажного воздуха. Все расчеты влажного воздуха ведут на 1 кг массы сухого воздуха, поскольку в процессе сушки только сухая часть влажного воздуха остаётся величиной постоянной.

Абсолютной влажностью воздуха называется масса водяного пара, содержащегося в 1 м³ влажного воздуха. Абсолютная влажность численно равна плотности водяного пара ρ_п при его парциальном давлении и температуре.

Отношение массы водяного пара, содержащегося в 1 м³ влажного воздуха ρ_п, к максимально возможной в том же объёме при том же давлении и при той же температуре ρ_н называется относительной влажностью воздуха

. (2.10)

При расчете процесса сушки оперируют параметром удельного влагосодержания d - массой водяного пара, отнесённой к 1 кг сухой части воздуха.

Величина удельного влагосодержания насыщенного воздуха (φ=1, р_п=р_s.) может быть определена из зависимости

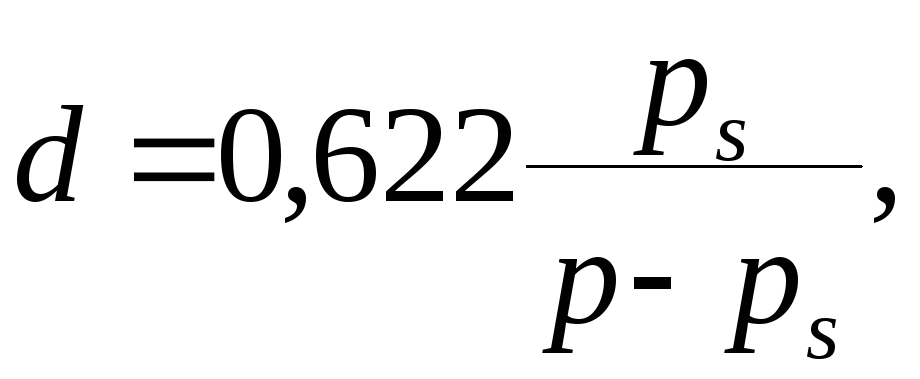(2.11)

где р, р_п – давление влажного воздуха и парциальное давление водяного пара следует подставлять в одних и тех же единицах измерения, предпочтительно в системе СИ – Н/м² (в МКГСС – кгс/см² или СГС- кгс/см², мм. рт. ст.).

Удельную энтальпию i (теплосодержание) влажного воздуха относят к 1 кг сухой части, т.е. определяют энтальпию смеси, состоящей из сухого воздуха (массой m_в=1кг) и водяного пара (m_п =d m_в).

(2.12)

где i_в - энтальпия сухого воздуха, кДж/кг; i_п - энтальпия пара, кДж/кг.

Энтальпия 1 кг сухого воздуха, кДж/кг,

(2.13)

где с_с.в – удельная изобарная теплоёмкость сухого воздуха, в приближённых расчетах в небольшом диапазоне температур с_с.в=1 кДж/(кг К); t – температура влажного воздуха, ^оС;

Энтальпия 1 кг пара i_п, кДж/кг, достаточно точно может быть вычислена по формуле, в которой теплота испарения воды q_п при 0^оС принята равной q_п=2500 кДж/кг, а удельная изобарная теплоёмкость пара с_р.п.=2 кДж/(кг К)

, (2.14)

тогда

. (2.15)

Параметры влажного воздуха весьма удобно определять при помощи диаграммы i-d влажного воздуха (см.рис.3 и прил.3).

Диаграмма i-d значительно упрощает решение различных задач, связанных с изменением состояния влажного воздуха.

В диаграмме i-d по оси абсцисс отложено влагосодержание d, а по оси ординат - энтальпия i влажного воздуха (на 1 кг сухого воздуха). Барометрическое давление принято равным В=745 мм рт. ст. – среднегодовое давление центральной полосы РФ.

Для более удобного расположения отдельных линий на диаграмме координатные оси в ней проведены под углом 135⁰.

В выполненных диаграммах наклонная ось влагосодержания не вычерчивается, а вместо неё из начала координат проводится горизонталь, на которую значения d спроектированы с наклонной оси. Поэтому линии энтальпии i идут наклонно, параллельно наклонной оси абсцисс, линии же d=const идут вертикально, параллельно оси ординат. В диаграмме построены изотермы (t=const).