Механическая работа, мощность и энергия

При поступательном движении элементарная работа силы равна скалярному произведению:

,

где—элементарное перемещение тела, α — угол между векторами и.

При конечном перемещении тела из точки (1) в точку (2) механическая работа:

.

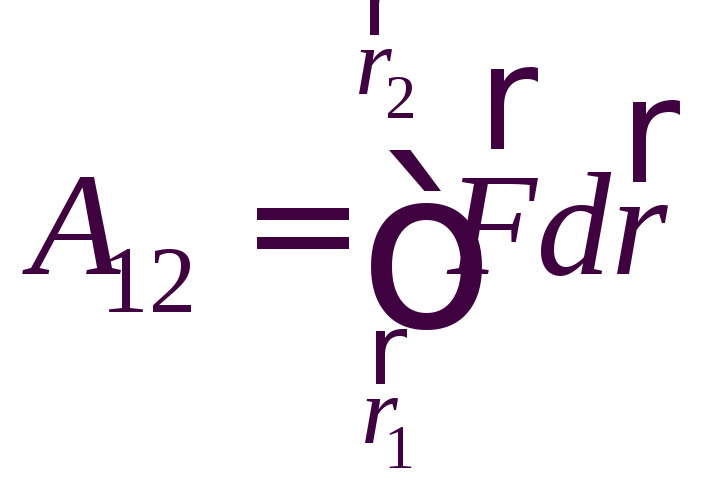В частном случае ,, получаем

,

где — путь, пройденный под действием силы .

При вращательном движении:

,

где — момент сил;— элементарный угол поворота тела.

При вращении тела от угла φ₁ до φ₂ механическая работа:

.

В частном случае, когда :

Мощность — скорость совершения работы.

Для поступательного движения:

,

где — скорость тела;α — угол между векторами силы и скорости.

Для вращательного движения:

,

где — угловая скорость.

Энергия — способность тела совершать работу.

Кинетическая энергия — энергия, связанная с движением тел.

Для поступательного движения:

,

где — масса;— скорость тела.

Для вращательного движения ,

где — момент инерции;— угловая скорость тела.

Потенциальная энергия — энергия, связанная с взаимодействием тел.

Потенциальная энергия тела массой , поднятого на высоту над поверхностью земли:

,

где — ускорение свободного падения.

Потенциальная энергия упругой деформированной пружины

,

где — коэффициент жесткости; — удлинение (сжатие) пружины.

Теорема об изменении кинетической энергии:

изменение кинетической энергии тела равно работеравнодействующей силы:

.

Работа потенциальных сил при перемещении материальной точки равна убыли ее потенциальной энергии:

.

Закон сохранения механической энергии:

если в замкнутой системе действуют только потенциальные силы, то

.

2. Примеры решения задач

1. Маховик, имеющий форму диска массой m = 5 кг и радиусом R = 0,2 м, свободно вращается с частотой n = 720 об/мин. При торможении маховик движется равнозамедленно и полностью останавливается через t = 20 с. Определить тормозящий момент М и число оборотов маховика N до полной остановки.

Дано: кг,м, об/с, с.

Определить: ,.

Решение:

Определим момент силы трения .

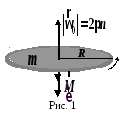
Торможение маховика происходит под действием момента сил трения (рис.1). По основному закону динамики вращательного движения

. (1)

Момент инерции диска:

. (2)

При равнозамедленном вращении угловая скорость меняется по закону:

,

где . Отсюда:

. (3)

Подставляя (2) и (З) в (1), получаем:

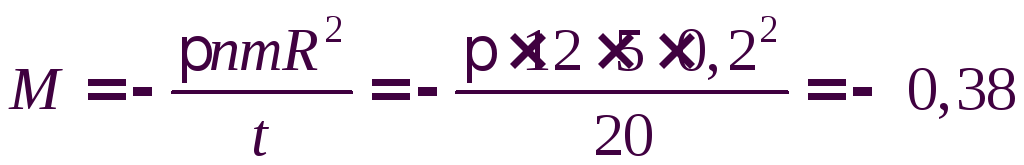(Нּм).

Знак (–) указывает, что угловое ускорение и момент силы трения направлены против начальной угловой скорости.

Определим число оборотов .При равнозамедленном движении угол поворота маховика до остановки:

.

Учитывая (3) и то, что , получаем:

(об).

Ответ: = 0,38 Нּм, = 120 оборотов.

2. Диск радиусом м и массой кг вращается вокруг вертикальной оси с частотой об/мин. В центре диска стоит человек массой кг. Какую линейную скорость v относительно пола помещения будет иметь человек, если он перейдет на край диска? Человека считать материальной точкой.

Дано: м, кг, кг,об/с. .

Определить: .

Решение:

По закону сохранения момента импульса

, (1)

где — момент инерции диска; и — моменты инерции человека в центре и на краю диска, соответственно; и угловые скорости диска с человеком, стоящим в центре и на краю диска, соответственно (см. рис. 2).

Связь линейной и угловой скорости:

. (2)

Выразив из уравнения (1) и подставив его в формулу (2), получим:

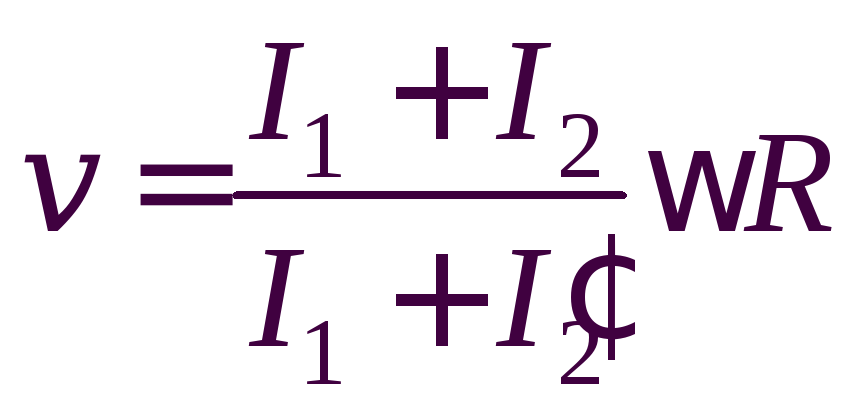. (3)

Момент инерции диска равен:

.

Момент инерции материальной точки (человека) равен:

, .

Угловая скорость диска до перехода человека:

.

Подставив в (3) выражения для ,,и, получим:

.

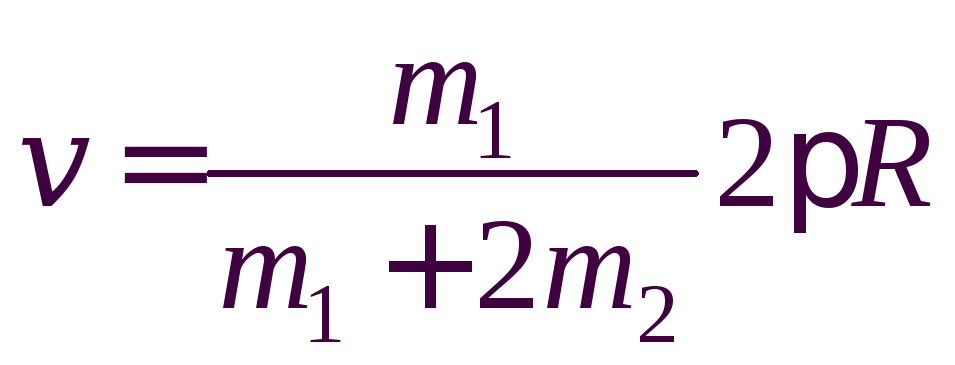Численный расчет:

(м/с).

Ответ: м/с.

3. Через блок, укрепленный на горизонтальной оси, перекинута нить, к концам которой прикреплены грузы кг и кг. Масса блока кг. Считая блок однородным диском, найти линейное ускорение системы .

Дано: кг, кг, кг.

Определить: .

Р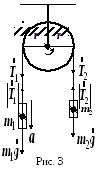ешение:

Расставим действующие на тела силы и моменты сил (рис.3).

На первое тело действуют сила тяжести и сила натяжения нити . На второе тело, аналогично, и .

На блок действуют момент силы :

,

и момент силы :

,

где — радиус блока.

После расстановки сил и их моментов к каждому телу можно применить основное уравнение динамики. Для первого тела в проекциях на направление движения:

, (1)

для второго тела

,(2)

для блока

или .(3)

Решая уравнения (1), (2) и (З) совместно относительно и учитывая, что , получаем:

.

Численный расчет: 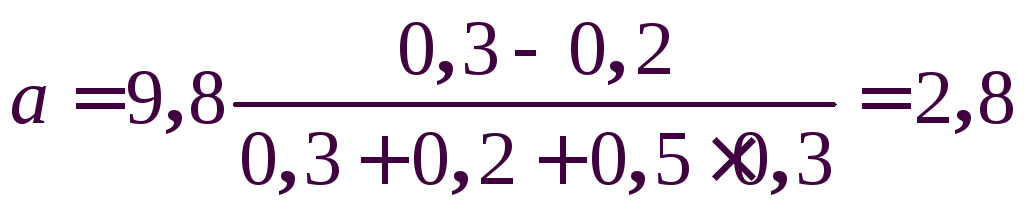м/с².

Ответ: м/с².

4. Найти кинетическую энергию велосипедиста, едущего со скоростью м/с. Масса велосипедиста вместе с велосипедом , причем на колеса приходится масса кг. Колеса велосипеда считать обручами.

Дано: , кг, м/с.

Определить:.

Решение:

Движение твердого тела можно представить, как поступательное движение центра инерции с кинетической энергией и вращательное движение тела вокруг оси, проходящей через центр инерции, с кинетической энергией . В нашем случае вращаются только колеса, поэтому полная кинетическая энергия велосипеда:

Связь линейной и угловой скоростей:

,

где — радиус колеса. Момент инерции обруча относительно оси, проходящей через его центр,

.

Подставляя и в формулу для полной кинетической энергии велосипеда, получаем:

.

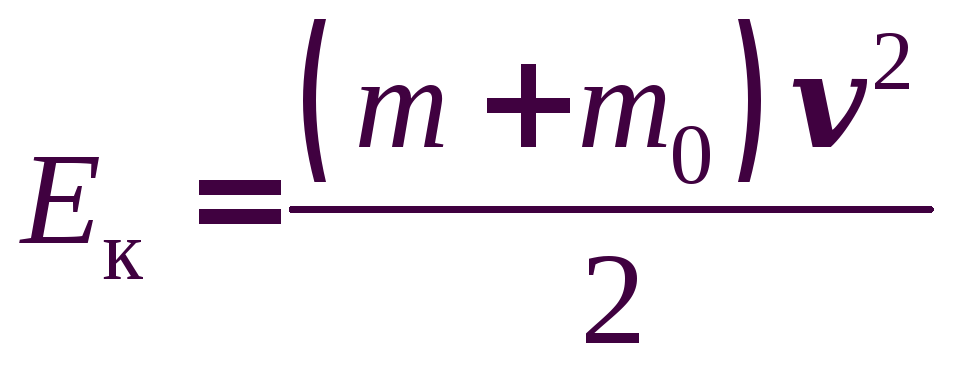Численный расчет: 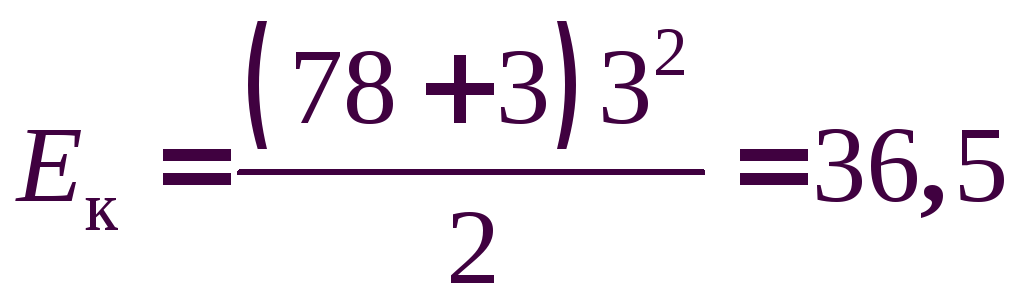(Дж).

Ответ: Дж.

5. По ободу шкива, насаженного на общую ось с колесом, намотана нить, к концу которой подвешен груз массой . На какое расстояние должен опуститься груз, чтобы колесо со шкивом вращалось с частотой об/мин? Момент инерции колеса кгּм², радиус шкива м.

Дано: , об/с, кгּм²,м.

Определить: .

Решение:

В начальный момент система обладала только потенциальной энергией(рис.4). Когда груз, опустился на высоту h, энергия системы складывается из кинетической энергии вращения колеса и кинетической энергии груза .

Если пренебречь силами трения, то в системе выполняется закон сохранения механической энергии:

.

Учитывая связь линейной и угловой скоростей:

,

получаем:

.

Отсюда:

.

Численный расчет:

(м).

Ответ: h = 0,86 м.

6. С наклонной плоскости скатывается без скольжения однородный диск. Найти силу трения, если угол наклона плоскости к горизонту , масса диска .

Дано: .

Определить: .

Решение:

На тело действуют три силы: сила тяжести, сила реакции опоры и сила трения (рис.5), но только сила трения имеет отличный от нуля момент относительно оси вращения O. При отсутствии диск соскальзывал бы с наклонной плоскости, не вращаясь.

Запишем основной закон динамики (для поступательного движения) в проекциях на ось X :

. (1)

Основной закон динамики для вращательного движения диска:

.

Учитывая, что , получаем:

.

Для диска: , поэтому:

. (2)

Решая (1) и (2) совместно, получаем:

.

Ответ: .

7. Какую работу совершает человек, поднимая тело массой на высоту с ускорением ?

Дано: ,.

Определить: .

Р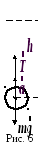ешение:

Р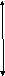абота при прямолинейном движении под действием постоянной силы:

В нашем случае ,,(рис. 6).

По второму закону Ньютона (в проекциях на направление ускорения):

.

Таким образом,

и .

Ответ: .

8. Найти работу , которую надо совершить, чтобы увеличить скорость движения тела массой от до на пути . На всем пути действует сила трения .

Дано: ,

Определить: А.

Решение:

И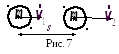зменение кинетической энергии тела равно работе всех сил, действующих на тело (рис. 7):

.

На тело действует две силы: сила тяги, совершающая положительную работу А, и сила трения, совершающая отрицательную работу .

Поэтому: .

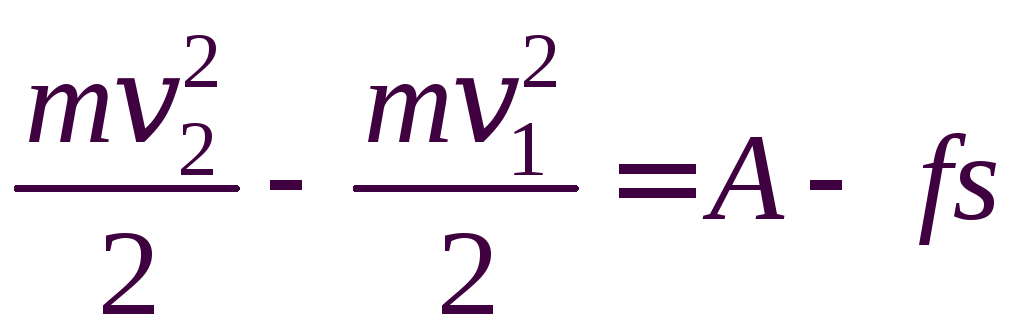Отсюда: .

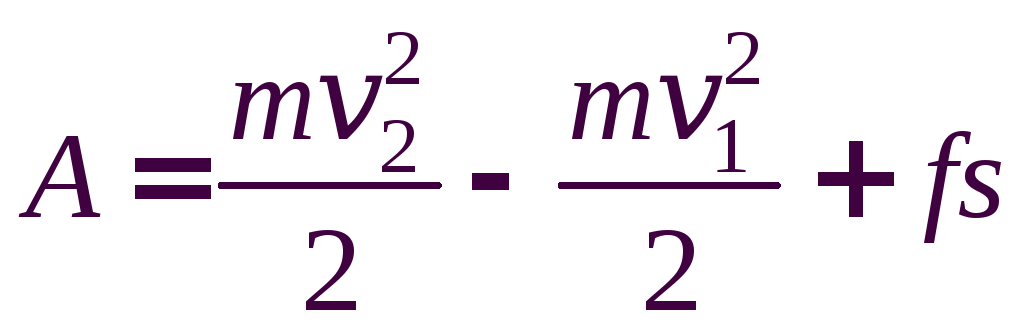Ответ: .

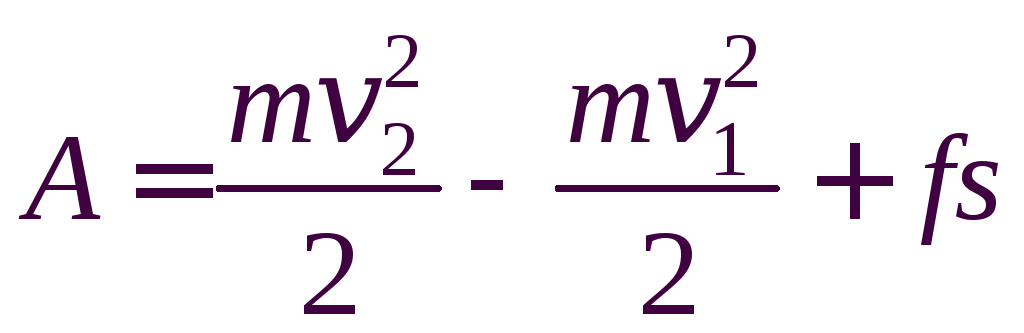9. Найти скорость вылета пули массой m из пружинного пистолета при выстреле вверх, если жесткость пружины k, а сжатие . На какую высоту поднимется пуля?

Дано: m, k, x.

Определить:,h.

Решение:

До выстрела энергия была сосредоточена в сжатой пружине (рис. 8):

.

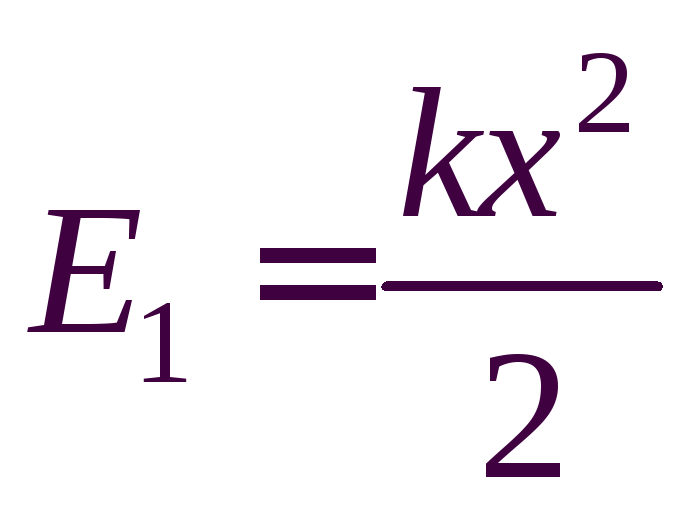Так как диссипативных взаимодействий нет, то по закону сохранения полной механической энергии в момент вылета пули из пистолета ее энергия складывается из потенциальной энергии гравитационного взаимодействия и кинетической энергии пули :

.

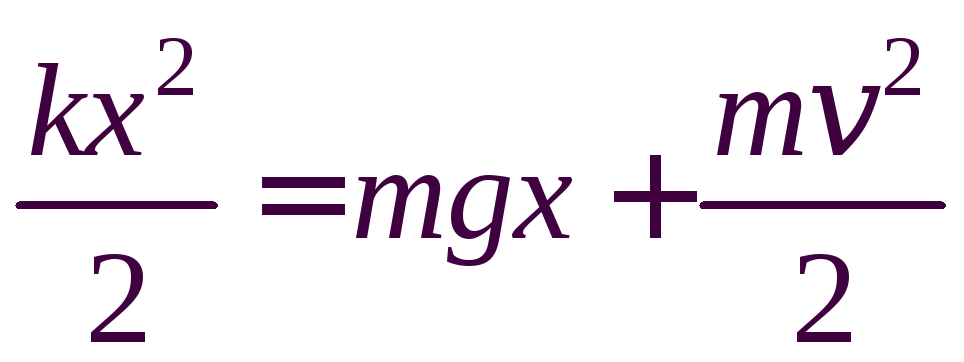Отсюда .

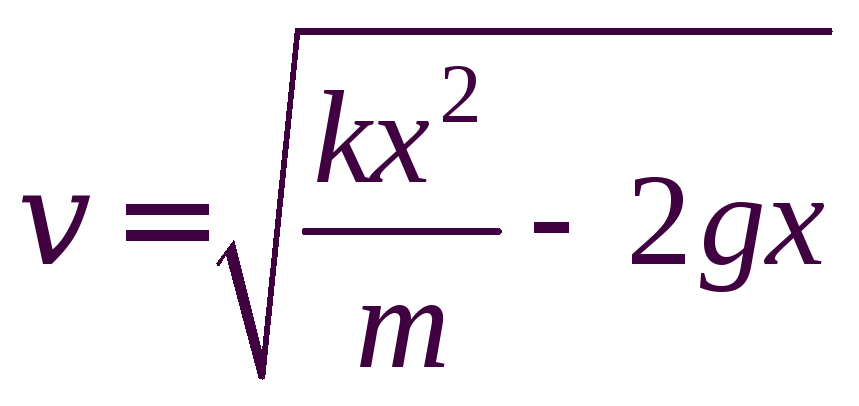В высшей точке подъема , поэтому .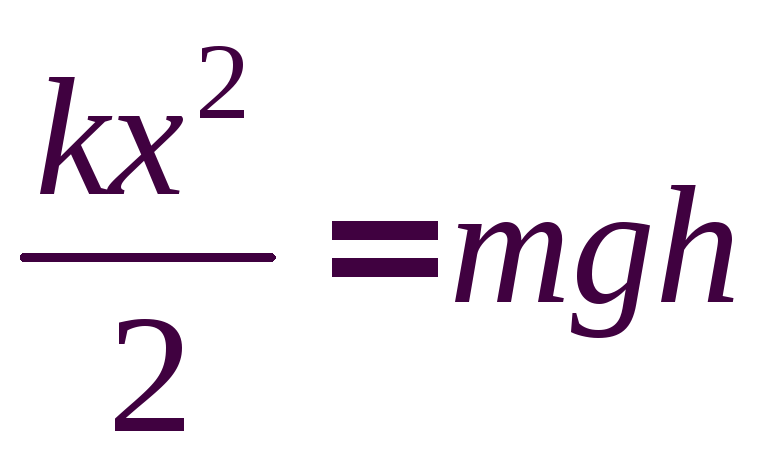

Следовательно, .

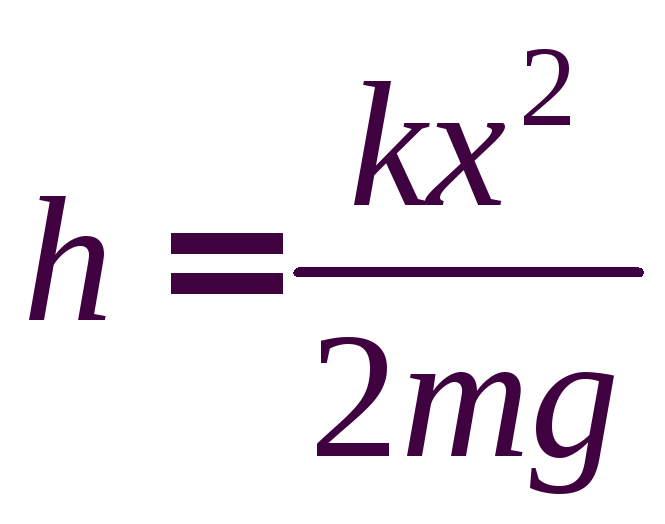Ответ:,.

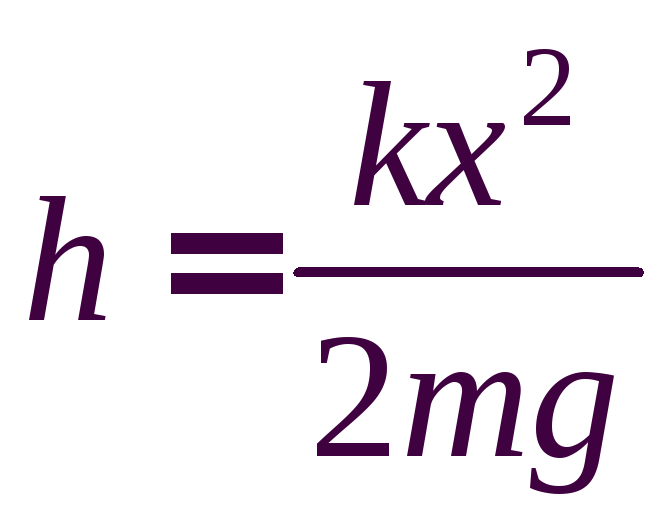10.Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули , масса шара , скорость пули . При каком наибольшем расстоянии l от центра шара до точки подвеса шар поднимется до верхней точки окружности?

Дано: , ,.

Определить: l.

Решение:

По закону сохранения механической энергии, кинетическая энергия шара с пулей должна быть равна их потенциальной энергии вточке максимального подъема (рис. 9):

. (1)

При неупругом соударении пули с шаром выполняется только закон сохранения импульса:

.

Отсюда: 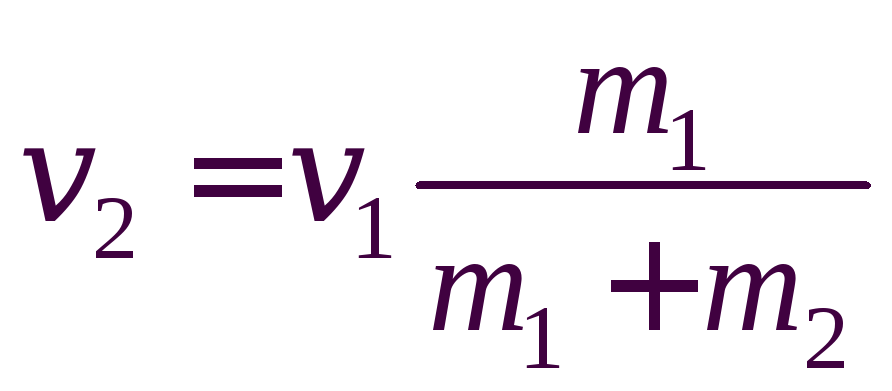. (2)

Подставляя (2) в (1), получаем .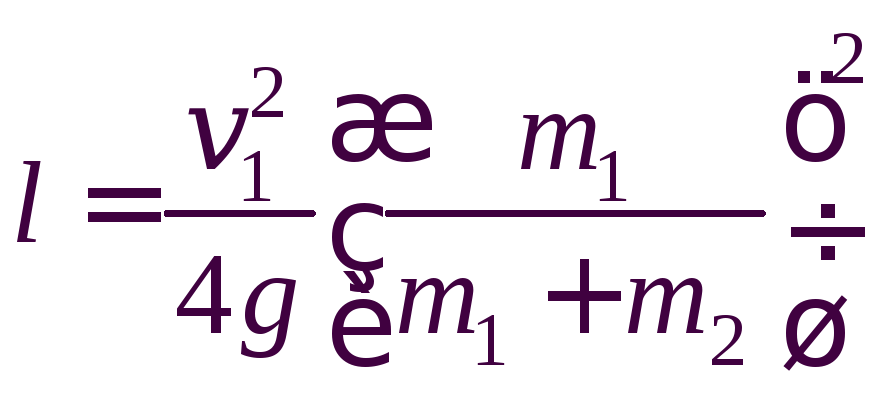

Ответ: .
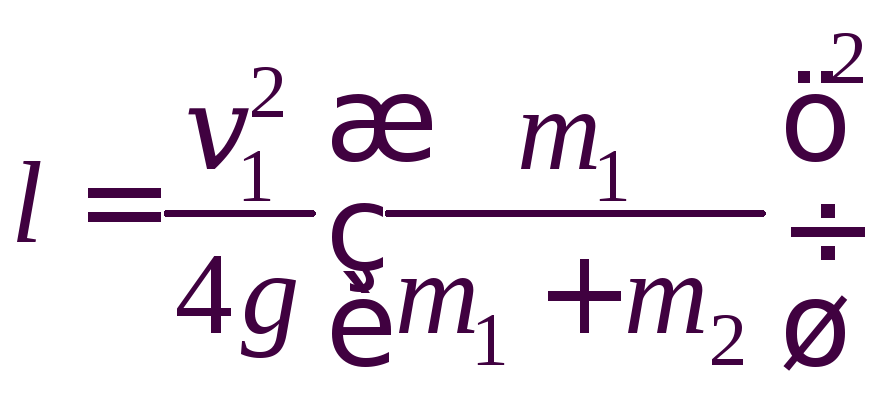