8. Вычисление длины дуги плоской кривой.
Длинна кривой линии – это предел длины вписанной в нее ломанной, когда длина наибольшего звена стремится к нулю. Если этот предел существует, то кривая называется спрямляемой.
Теорема.
Пусть дана непрерывная, дифференцируемая
на
функция
.
Следовательно, ее производная тоже
непрерывна, причем
.
Тогда длина дуги графика функции
определяется выражением
Доказательство.
Согласно рисунку,
.
Отсюда длина элементарной дуги будет
равна
.
Длина всей дуги будет равна
Пример
9. Найти длину окружности.
Имеем
,
отсюда следует, что
.
Найдем производную
.
Следовательно, длина окружности будет
равна
Кривая задана параметрически.
В этом случае
. Тогда
.
Следовательно
И, соответственно
Пример 10.
Найти длину дуги
Имеем
,
.
Длина дуги будет равна
Кривая задана в полярных координатах, что представляет собой частный случай параметрического задания кривой, где параметром выступает угол .
В этом случае:
,
.
Далее
,
.
Подынтегральное выражение будет равно:
Таким образом, длина дуги в полярных координатах будет определяться выражением
Пример 11. Вычислить длину кардиоиды .
Имеем
.
Тогда
9. Вычисление объёма тела по площади поперечного сечения.
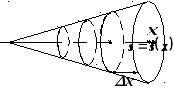
Пусть
нам дано тело, известные площади
поперечного сечения
которого расположены перпендикулярно
оси
,
как показано на рисунке.
Тогда элементарный объем этого тела будет равен
Соответственно полный объем этого тела будет выражаться формулой
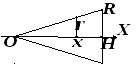
Например,
найти объем конуса, высоты
и радиуса основания
.
Согласно рисунку запишем
Следовательно, площадь произвольного сечения будет равна
Тогда объем конуса будет равен
10. Вычисление объем тела вращения.
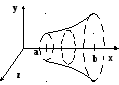Формула
для объема получается из предыдущей,
где
.
Пример 12.
Найти объем эллипсоида с осями
,
,
.
Имеем уравнение
эллипсоида
.
Для какой-то произвольной точки
запишем
То есть в произвольном
сечении
мы получили эллипс с полуосями
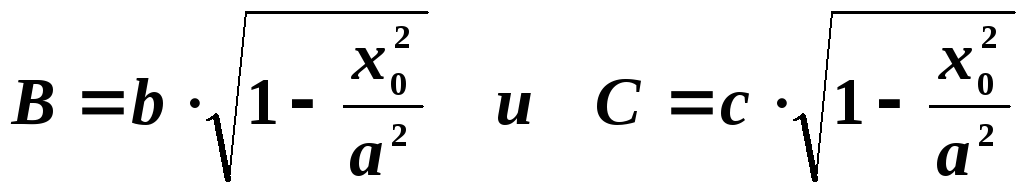
Площадь эллипса равна
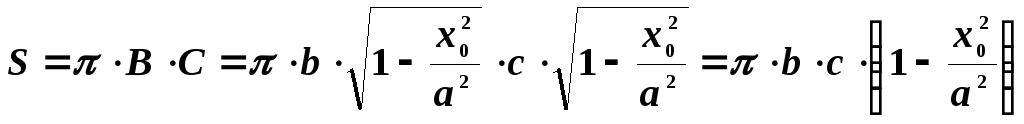
Следовательно, объем эллипсоида будет равен
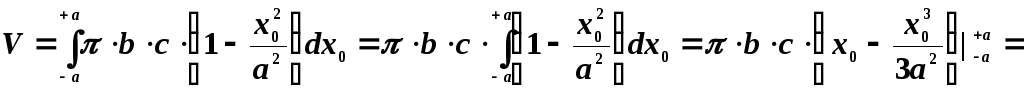
1 Y y y y 1. Приближенное вычисление определенного интеграла
Пусть надо вычислить определенный интеграл от непрерывной на отрезке функции и при этом первообразная нам неизвестна.
Простейший способ приближенного вычисления интеграла вытекает из его определения
Эта формула называется квадратурной формулой прямоугольников, поскольку площадь фигуры под графиком функции мы разбиваем на элементарные прямоугольники.
Можно площадь фигуры разбивать не на прямоугольники, а на трапеции, образованные секущими. В этом случае приближенное значение интеграла будет рассчитываться как
FVB