7. Вычисление площадей плоских фигур

а) Площадь криволинейной трапеции (явное задание функции).

Зададим на отрезке (и- конечные числа) неотрицательную, непрерывную функцию, график которой изображен на рисунке.

Произведем разбиение отрезка на- частей точками

Выберем на каждом из полученных частичных отрезков () по произвольной точке. Определим значения функциив этих точках и составим сумму

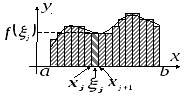
которую называют интегральной суммой и которая, очевидно, равна сумме площадей заштрихованных прямоугольников, как показано на рисунке.

Предел, к которому стремится интегральная сумма, когда называется определенным интегралом от функциина отрезке

Если функцияотрицательна внутри отрезка , то интеграл по абсолютному значению равен площади, покрываемой графиком, но имеет отрицательное значение (см. рис.).

Пусть теперьменяет знак на интервале , как показано на рисунке.

В этом случае определенный интеграл будет подсчитываться как

Н

апример, найти площадь фигуры, ограниченной линиейв пределах интервала, где,(см. рисунок). Имеем.

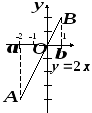
Это число равно разности площадей

и

б) Параметрическое задание функции.

Пусть кривая , ограничивающая исследуемую фигуру, задана параметрически:. В этом случае дифференциалбудет равен:. И, следовательно, площадь фигуры будет определяться следующим выражением:

где .

Например, надо найти площадь эллипса. Уравнение эллипса в параметрическом виде записывается как

Действительно:

Отсюда

Тогда четвертая часть площади эллипса (в первом квадранте) будет рассчитываться как

Отсюда площадь эллипса равна .

в) Площадь криволинейного сектора (кривая в полярных координатах) дается формулой

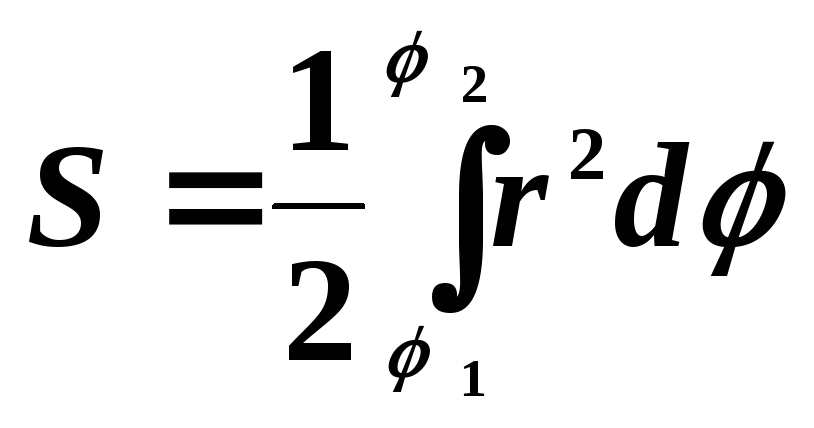
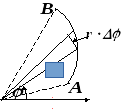
Действительно, согласно рисунку, площадь элементарного сектора представляет собой площадь треугольника, равную половине произведения основания на высоту

Отсюда вытекает основная формула.

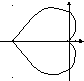
Пример 8. Найти площадь фигуры, ограниченной кривой - Кардиоида

Отсюда площадь кардиоиды равна.

8. Вычисление длины дуги плоской кривой.

Длинна кривой линии – это предел длины вписанной в нее ломанной, когда длина наибольшего звена стремится к нулю. Если этот предел существует, то кривая называется спрямляемой.

Теорема. Пусть дана непрерывная, дифференцируемая на функция. Следовательно, ее производная тоже непрерывна, причем. Тогда длина дуги графика функции определяется выражением

Доказательство. Согласно рисунку, . Отсюда длина элементарной дуги будет равна. Длина всей дуги будет равна

Пример 9. Найти длину окружности.

Имеем , отсюда следует, что. Найдем производную. Следовательно, длина окружности будет равна

Кривая задана параметрически.

В этом случае . Тогда. Следовательно

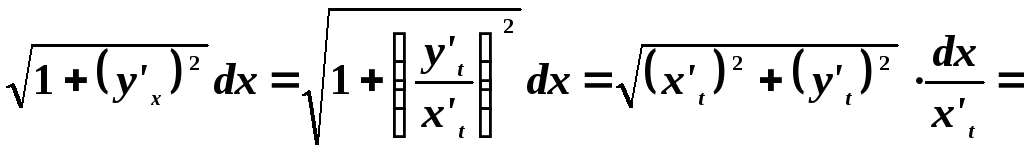
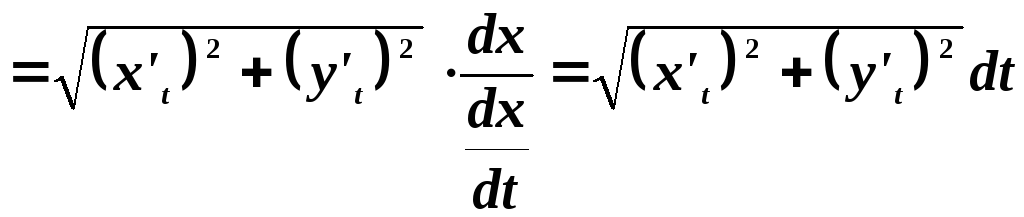
И, соответственно

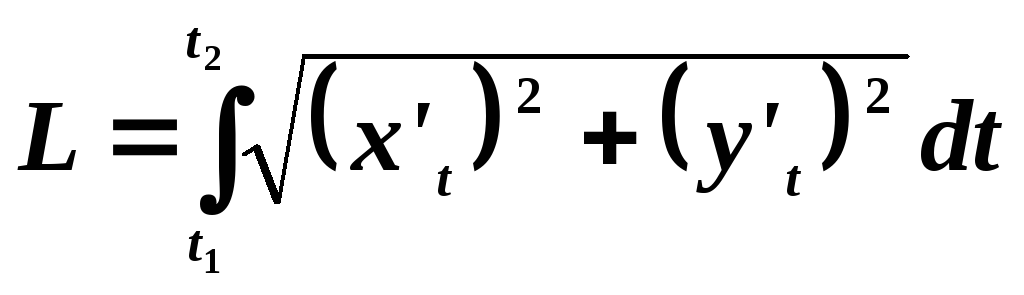
Пример 10.

Найти длину дуги

Имеем ,.

Длина дуги будет равна

Кривая задана в полярных координатах, что представляет собой частный случай параметрического задания кривой, где параметром выступает угол .

В этом случае: ,.

Далее ,.

Подынтегральное выражение будет равно:

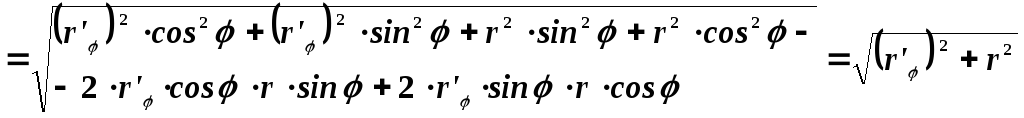
Таким образом, длина дуги в полярных координатах будет определяться выражением

Пример 11. Вычислить длину кардиоиды .

Имеем . Тогда