34. Властивості середньої (математичні).

1)aлгебраїчна сума відхилень всіх варіант від середньої дорівнює 0:

2) Якщо одну із варіант збільшити або зменшити на певну величину, то і середня зміниться на таку ж величину:

3) Якщо кожну варіанту розділити чи помножити на довільне число, то і середня збільшиться або зменшиться на те ж саме число

4) Якщо частоти всіх варіант помножити чи поділити на довільне число, то середня не зміниться

5) Сума квадратів відхилень варіант від середньої менша за будь-яку іншу величину

35. Середні структурні

До середніх структурних відносяться дві величини, які називаються "мода" і "медіана".Структурні величини мода і медіана застосовуються для вивчення внутрішньої будови рядів розподілу, тобто їх структури.

36. Середня гармонійна

Середня гармонійна величина використовується у тому випадку, якщо відомі обернені значення осереднюваного показника. Середня гармонічна — це обернена до середньої арифметичної із обернених значень ознак. її обчислюють, коли необхідно осереднення обернених індивідуальних значень ознак шляхом їх підсумування (наприклад, у випадках визначення середніх витрат часу, праці, матеріалів на одиницю продукції тощо). У випадку розрахунку середньої гармонічної зваженої її обчислюють тоді, коли відомі дані про загальний обсяг ознаки (z = xf), а також індивідуальні значення ознаки (х), невідома є частота (f). Формули середньої гармонічної - простої і зваженої — мають такий вигляд:

- для простої: Хсер = n / ∑1 / x

- для зваженої: Хсер =∑z / ∑z / x

37. Середня арифметична

Середня арифметична - це найпоширеніший вид середньої між інших. Вона застосовується тоді, коли відомі індивідуальні значення усереднюваної ознаки та їх кількість у сукупності. Тоді проста середня арифметична обчислюється діленням загального обсягу значень ознаки на обсяг сукупності:

Хсер = (x1 + x2 + … + xn) / n = ∑x / n

38. Мода:сутність,методика визначення

Мода (М0) — це значення ознаки, що найчастіше зустрічається у сукупності. Таким чином, у дискретному ряді розподілу - це варіанта, що має найбільшу частоту. В інтервальному ряді розподілу мода знаходиться за формулою:

де: хмо — нижня межа модального інтервалу;

і — величина модального інтервалу;

f2, f1, f3 — відповідно частота модального, передмодального та після модального інтервалів

39. Медіана:сутність,методика визначення

Медіана (Ме) — це значення ознаки, що ділить рангований ряд значень показника на дві рівні частини. У першої половини одиниць значення ознаки менше медіани, а у другої — більше. Тобто, медіана — це серединне значення

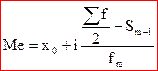
40.Поняття варіації,показники варіації

Варіацією в статистиці називають кількісні зміни величини досліджуваної ознаки в межах однорідної сукупності, які зумовлені впливом дії різних факторів.

Показники

• розмах варіації становить різницю між мінімальним і максимальним значенням ознаки: R = xmax – xmin.

• Середнє лінійне відхилення являє собою середню арифметичну з абсолютних значень відхилень окремих варіант від середньої арифметичної.

• Дисперсією називають середній квадрат відхилень індивідуальних значень ознаки від середньої арифметичної. її визначають за формулами:

• Середнє квадратичне відхилення одержують шляхом добування кореня квадратного з дисперсії:

• Коефіцієнт варіації