Работы и.А. Вышнеградского

Во второй половине XIX в. только в Англии работало более 75000 паровых машин, управляемых простыми центробежными регуляторами Уатта и в промышленности часто сталкивались со случаями нарушения устойчивости системы «паровая машина - регулятор».

В 1868 г. появилась работа английского физика Джеймса Клерка Максвелла, в которой он впервые не только составляет уравнение движения, но и, переходя к малым колебаниям относительно исследуемого равновесия, линеаризует их. Он показывает, что вопрос о движении системы «паровая машина - регулятор» сводится к анализу линейных дифференциальных уравнений третьего порядка с постоянными коэффициентами, а вопрос об устойчивости движения - к анализу расположения корней характеристического уравнения относительно мнимой оси. И все же, несмотря на это, работа Максвелла не ответила на вопросы инженеров и не сняла трудностей, возникавших в промышленности. Дело в том, что Максвелл рассматривал регуляторы, которые мы теперь называем астатическими, в то время как на практике повсеместно применялись статические регуляторы, и, кроме того, в уравнении машины учел эффект, который теперь называют самовыравниванием, пренебрежимо малый в машинах тех лет.

Задачу заново поставил Иван Алексеевич Вышнеградский.

Вышнеградский И.А. (1832-1895) родился в г. Вышний Волочек. После окончания (1851) физико-математического факультета Главного педагогического института в Петербурге преподавал во 2-м Петербургском кадетском корпусе. С 1862 г. профессор механики Михайловской артиллерийской академии. С 1875 г. директор Петербургского технологического университета. Ввел преподавание курса теоретических основ машиностроения. В Петербургском технологическом университете и Михайловской артиллерийской академии Вышнеградский читал курсы прикладной механики, термодинамики, теории упругости и др. В 1860 г. опубликовал руководство «Элементарная механика», в течение многих лет считавшееся лучшим в России. Со 2-ой половины 70-х годов Вышнеградский постепенно отходит от научной деятельности и принимает участие в частных капиталистических компаниях. В 1888-1892 гг. министр финансов России.

В своей работе «О регуляторах прямого действия» (1877) Вышнеградский дал метод расчета регуляторов Уатта.

Вышнеградский рассматривает систему «паровая машина - регулятор» и полагает, для большей полноты и общности исследования, что регулятор снабжен катарактом (рис. 305), т.е. прибором, который приходит в движение вместе с муфтой регулятора и производит при этом на муфту давление, зависящее от ее скорости и противоположное направлению ее движения. В виде такого катаракта обыкновенно употребляется поршень, который может двигаться в закрытом с обоих концов цилиндре, наполненном жидкостью, которая при движении поршня вытесняется с одной его стороны на другую, проходя при этом через отверстие, которое можно произвольно регулировать.

Вышнеградский:

1. Отбросил все нелинейности в регуляторе, в том числе и кулоновское трение в муфте и сочленениях регулятора;

2. Предположил, что паровая машина обладает непрерывным подводом энергии, и принял линейную пропорциональность между смещением заслонки и действующим моментом;

3. Принял, что разным нагрузочным моментам соответствуют разные установившиеся угловые скорости системы «машина - регулятор», т.е., говоря инженерным языком, принял, что регулятор имеет определенную, не равную нулю неравномерность;

4. Отбросил саморегулирование машины и зависимость нагрузочного момента от числа оборотов;

5. Принял постоянство момента инерции в уравнении движения главного вала машины.

Условие сходимости процесса регулирования Вышнеградский сводит к условиям, которым должны удовлетворять коэффициенты характеристического уравнения

чтобы все его корни имели отрицательные действительные части.

Как известно, эти условия сводятся к одному неравенству

(это следует из формулы Кардано),

где M - коэффициент, характеризующий вязкое трение в муфте и сочленениях регулятора;

I - момент инерции главного вала;

kLg - мера подвижности регулятора (коэффициенты, зависящие от конструкции регулятора и его связи с машиной);

N - коэффициент, характеризующий неравномерность регулирования;

₀ - установившаяся угловая скорость.

Вышнеградский дает замечательную геометрическую интерпретацию полученных им условий устойчивости, имеющую значение, выходящее за пределы рассматриваемой им задачи и позволяющую придать геометрический смысл проблеме об условиях отрицательности действительных корней алгебраического уравнения. Именно Вышнеградский в характеристическом уравнении переходит к новым переменным, полагая

, ,

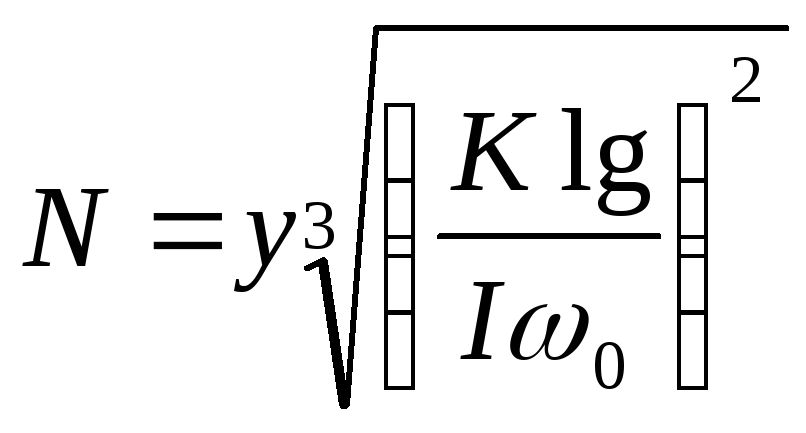
получает кубическое уравнение

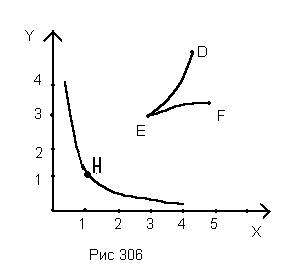
зависящее от двух параметров x и y, и строит знаменитую «диаграмму Вышнеградского», откладывая по прямоугольным осям параметры x и y. Для этих параметров условия устойчивости имеют вид x*y>1, и, следовательно, на плоскости параметров гипербола x*y=1 (так называемая «гипербола Вышнеградского») отделяет область значений x и y, соответствующую устойчивой работе системы «машина - регулятор», от области, где имеет место неустойчивость (рис. 306).

Однако содержание работы Вышнеградского не ограничивается лишь вопросами устойчивости прямого регулирования паровой машины. В опубликованном почти одновременно с русским оригиналом немецком переводе этой работы имеется дополнительный параграф. В этом параграфе Вышнеградский занимается не устойчивостью регулирования, а качеством переходного процесса. Он определяет условие, при которых во время переходного процесса, вызванного мгновенным сбросом нагрузки, угловая скорость машины претерпевает конечное или бесконечное число колебаний. Вышнеградский находит уравнение кривой, которая на диаграмме Вышнеградского отделяет параметры, соответствующие монотонным переходным процессам и процессам с конечным числом колебаний от параметров, при которых переходный процесс сопровождается бесконечным числом колебаний.

Уравнение

рассматривая которое, легко приходим к заключению, что уравнение

будет иметь все три корня вещественные, если

y²x²-4(y³+x³)+18xy-27>0

и два корня будут комплексные, если

y²x²-4(y³+x³)+18xy-27<0

Для x и y, отвечающим точкам, лежащим на этой кривой, корни этого уравнения будут вещественными, и притом два из них будут равны между собой, а для одной из таких точек, именно для x=3, y=3 все три корня рассматриваемого уравнения будут равны между собой.

Построенные на основании предыдущих исследований две кривые DEF и GHK делят угол между положительными направлениями осей координат на три части.

Первая, заключающаяся между ветвями DE и EF кривой DEF, содержит точки, которым соответствуют такие регуляторы, которые, будучи раз выведены из равновесного положения, начинают двигаться без всяких колебаний, постепенно и безгранично приближаясь к новому равновесному положению.

Вторая, заключающаяся между кривой DEF и гиперболой GHK, содержит в себе точки, которым соответствуют такие регуляторы, которые, будучи один раз выведены из своего равновесного положения, получают колебания, которые, постепенно уменьшаясь с течением времени, приближают их безгранично к новому равновесному значению.

Третья, заключающаяся между гиперболой GHK и осями координат, содержит в себе точки, которым соответствуют такие регуляторы, что они, будучи один раз выведены из равновесного положения, затем постоянно с течением времени увеличивают свои размахи, сообщая машине совершенно неправильное движение.

Таким образом, диаграмма Вышнеградского дает совершенно простое средство отличить виды регуляторов. Из рассмотренного прямо вытекают такие следствия:

1. Регуляторы астатические (для которых N=0, а, следовательно, y=0), каким бы катарактом они ни были снабжены, не годятся для регулирования машин.

2. Регуляторы, хотя и статические, но не снабженные катарактом (для которых M=0, а, следовательно, и y=0) не годятся для регулирования машин.

Ко всякому данному статическому регулятору (для которого дано отличающееся от нуля N, а, следовательно, и y) можно подыскать такой катаракт (можно найти такое значение для x, а, следовательно, и для M), что этот регулятор не будет с течением времени безгранично увеличивать свои размахи.

После работы Вышнеградского динамика простейшей схемы регулирования - схемы Уатта - стала предельно прозрачной. Возникло отчетливое понимание, что машина и регулятор - это одно целое, что при переходных режимах возможно возникновение самораскачивания системы «машина - регулятор» и, что особенно важно, у инженеров возникло понимание, в какую сторону влияют изменения тех или иных конструктивных параметров этой системы на возникновение такого самораскачивания.