5. Взаимное расположение прямых в пространстве. Условие принадлежности двух прямых одной плоскости

Пусть прямые заданы каноническими уравнениями:

	,
	.

5.1.		-
		условие параллельности прямых
5.2.
		-
		условие перпендикулярности прямых
5.3.

5.4. Пусть ,,,,

.

Прямые илежат в одной плоскости, если векторы,,компланарны,

т.е. .

Следовательно, это условие, при котором илежат в одной плоскости.

Типовой пример. Прямая определяется точкамии. Прямаяесть пересечение двух плоскостей:. Доказать, что.

►Если прямые перпендикулярны, то перпендикулярны и их направляющие векторы. В качестве направляющего вектора прямой а -можно взять;= (-5; -9; 7). Направляющий вектор прямойb – – перпендикулярен каждой из двух плоскостей. Это означает, чтоперпендикулярен нормали первой плоскости, и перпендикулярен нормали второй плоскости. Но тогдаравен векторному произведению, т.е.=[,], или

=, или, что все равно,= (-4; 3; 1).

Найдем скалярное произведение (,)=20 – 27 +7 = 0, следовательно. Направляющие векторы двух прямых взаимно перпендикулярны, следовательно, соответствующие прямые также перпендикулярны. ◄

§5. Прямая и плоскость в пространстве. Условие принадлежности прямой плоскости

Пусть плоскость задана общим уравнением , а прямаязадана каноническими уравнениями .

1.
		-
		условие параллельности прямой и плоскости.
2.
		-
		условие перпендикулярности прямой и плоскости
3.	. Пусть векторы ивыходят из точки
	Следовательно,

Типовой пример. Написать уравнения прямой, проходящей через две точки: ,. Найти точку пересечения этой прямой с плоскостью:.

►Пусть – текущая точка прямой. Тогда.,. Условие параллельности двух векторов – пропорциональность их координат, значит

: – канонические уравнения прямой.

В параметрической форме: , получаем:.

Находим точку пересечения прямой с плоскостью, назовем эту точку. Это значит, нужно решить систему уравнений:

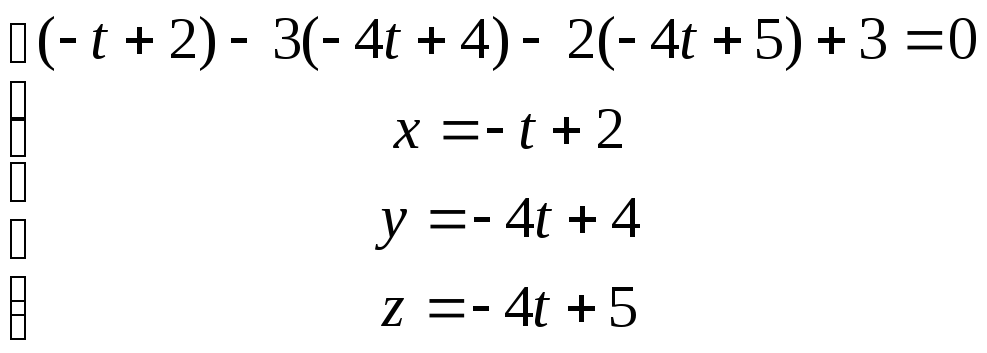
. Итак, .◄

Типовой пример. Найти расстояние от точки А (4; 3; 10) до прямой

: .

►Найдем проекцию точки на прямую. Назовем ее точкой. Точкаесть точка пересечения прямойс перпендикулярной ей плоскостью, проходящей через. Тогда: направляющий вектор прямой, его можно взять в качестве вектора-нормали плоскости,.

Напишем уравнение плоскости , проходящей через точку, с:, или.

Решая систему уравнений, находим точку :

(3; 6; 8).

Расстояние от точки до прямойесть длина вектора, получаем◄

Типовой пример. Найти точку , симметричную точке, относительно плоскости.

► 1) Напишем уравнения прямой , проходящей через точку, параллельной вектору.

.

2) Найдем точку -точку пересечения прямой с плоскостью.

Решим систему уравнений ,

Запишем параметрические уравнения прямой .

Подставим в первое уравнение системы , получим уравнение

или ; ; ,

т.е. –координаты точки .

3) Так как точка -середина отрезка , то

. Аналогично, ,.

Таким образом, -искомая точка.◄