§ 3. Плоскость

1. Общее уравнение плоскости. Пусть заданы: система координат , плоскость, точкаи вектор. Произвольная точкапринадлежит плоскоститогда и только тогда, когда векторыибудут перпендикулярны, т.е.. Координаты векторов:,. Следовательно,

(1) – уравнение плоскости, проходящей через данную точку, перпендикулярной данному вектору, где – текущие координаты;- координаты точки;– координаты вектора. Преобразуем уравнение(1).

. Получим (2) – общее уравнение плоскости .

Из общего уравнения получаем вектор , называемыйнормальным вектором плоскости .

Типовой пример. Составить уравнение плоскости, проходящей через точку перпендикулярной вектору.

►Применяя уравнение (1), получим: ;

или – это и есть общее уравнение плоскости. ◄

2. Расположение плоскости в пространстве. Уравнение плоскости в отрезках на осях

Рассмотрим частные случаи расположения плоскости , определяемой общим уравнением:.

1. Если ,то.

, то .

Если , то.

Если , топроходит через начало координат.

2. Если , то.

Если , то.

Если , то.

3. Если , топроходит через ось.

Если , топроходит через ось.

Если , топроходит через ось.

4. Если – это уравнение плоскости.

Если – это уравнение плоскости.

Если – это уравнение плоскости.

5. Если, то уравнение плоскостиможно привести к виду:или. Обозначив,

получим (3) –уравнение плоскости в отрезках на осях,

где ,,– точки пересечения с осями координат.

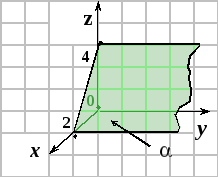
Типовые примеры. Построить плоскости, заданные общими уравнениями:

1.

.

2. .	3. .
4. .	5. .

3. Уравнение плоскости, проходящей через три точки

Пусть даны точки ,,принадлежащие плоскости.

Точка - произвольная точка плоскости. Построим векторы:,

,

.

Так как точки лежат в одной плоскости, то векторы компланарны. Следовательно, их смешанное произведение равно нулю.

(4)	- уравнение плоскости, проходящей через три точки.

Типовой пример. Составить уравнение плоскости , проходящей через точки,,.

►Пусть - текущая точка плоскости, следовательно,, векторы, а значит их смешанное произведение равно нулю:.

, ,.

Смешанное произведение этих векторов в координатной форме

.

, раскрыв скобки и приведя подобные члены, получаем уравнение плоскости :- общее уравнение плоскости, – уравнение плоскости в отрезках на осях.◄

Типовой пример. Составить уравнение плоскости, проходящей через точки ,,.

► Используем уравнение (4):

. ◄

5. Пучок плоскостей

Пусть плоскости ипересекаются по прямойa.

Плоскости, проходящие через линию пересечения двух плоскостей, образуют пучок плоскостей. Уравнение пучка плоскостей: .

Чтобы написать уравнение какой-либо плоскости пучка, достаточно знать точку, через которую она проходит.

Типовой пример. Написать уравнение плоскости , проходящей через линию пересечения плоскостейи, и через точку.

►Запишем уравнение пучка плоскостей: .

Значениеопределяем из условия, что плоскость проходит через точку:, или.

Следовательно, искомое уравнение имеет вид:

или . ◄