
- •Глава 4 векторная алгебра и аналитическая геометрия
- •§1. Векторная алгебра
- •§ 2. Системы координат на плоскости
- •§ 3. Прямая на плоскости
- •1. Общее уравнение прямой на плоскости
- •2. Частные случаи расположения прямой на плоскости.
- •3. Уравнение прямой, проходящей через данную точку: а) параллельной данной прямой; б) перпендикулярной данной прямой
- •4. Уравнение прямой, проходящей через две точки
- •5. Каноническое уравнение прямой
- •6. Параметрическое уравнение
- •7. Уравнение прямой с угловым коэффициентом
- •8. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой
- •Расстояние от точки до прямой на плоскости (второй способ)
- •0 1 2 3 4 5
- •§ 3. Плоскость
- •2. Расположение плоскости в пространстве. Уравнение плоскости в отрезках на осях
- •3. Уравнение плоскости, проходящей через три точки
- •5. Пучок плоскостей
- •6. Взаимное расположение плоскостей. Расстояние от точки до плоскости
- •§ 4. Прямая в пространстве
- •1. Общие уравнения прямой
- •3. Параметрические уравнения прямой
- •4. Уравнения прямой, проходящей через две точки
- •5. Взаимное расположение прямых в пространстве. Условие принадлежности двух прямых одной плоскости
- •§5. Прямая и плоскость в пространстве. Условие принадлежности прямой плоскости
- •§ 6. Линии второго порядка на плоскости
- •§7. Поверхности второго порядка
§ 2. Системы координат на плоскости
1 .
Прямоугольная система координат на
плоскости
определяется заданием масштабной
единицы измерения длин и двух взаимно
перпендикулярных осей
.
Прямоугольная система координат на
плоскости
определяется заданием масштабной
единицы измерения длин и двух взаимно
перпендикулярных осей
![]() (ось
абсцисс),
(ось
абсцисс),
![]() (ось
ординат),
пересекающихся
в одной точке
(ось
ординат),
пересекающихся
в одной точке
![]() ,называемой
началом
координат.
,называемой
началом
координат.
Возьмем
произвольную точку
![]() плоскости
и проведем через нее прямые, перпендикулярные
осям координат.
плоскости
и проведем через нее прямые, перпендикулярные
осям координат.
Эти
прямые пересекают оси координат
соответственно в точках
![]() ,
,
![]() .
Первой координатой
.
Первой координатой
![]() точки
точки
![]() ,ее абсциссой,
называется
длина отрезка
,ее абсциссой,
называется
длина отрезка
![]() ,
взятая со знаком плюс, если отрезок
,
взятая со знаком плюс, если отрезок![]() направлен в ту же сторону, что и ось
направлен в ту же сторону, что и ось![]() ,
и со
знаком минус – если в противоположную.
Аналогично, ординатой
,
и со
знаком минус – если в противоположную.
Аналогично, ординатой
![]() точки
точки
![]() называется
длина отрезка
называется
длина отрезка
![]() ,
взятая со
знаком плюс или минус.
,
взятая со
знаком плюс или минус.
Оси
координат разбивают координатную
плоскость на четыре части, которые
называются четвертями.
Например, в первой четверти
![]() .
.
2 .
Полярная система координат
определяется
заданием масштабной единицы измерения
длин, точкой
.
Полярная система координат
определяется
заданием масштабной единицы измерения
длин, точкой
![]() ,
называемойполюсом,
и лучом
,
называемойполюсом,
и лучом
![]() ,
называемымполярной
осью.
,
называемымполярной
осью.
Пусть
задана полярная система координат и
произвольная точка
![]() на плоскости. Полярными координатами
точки
на плоскости. Полярными координатами
точки![]() называются числа
называются числа![]() и
и![]() .
.![]() –
расстояние от точки
–
расстояние от точки![]() до полюса, называетсяполярным
радиусом.
до полюса, называетсяполярным
радиусом.
![]() –
угол, на который нужно повернуть полярную
ось до совмещения с лучом
–
угол, на который нужно повернуть полярную
ось до совмещения с лучом![]() ,
называетсяполярным
углом. Точка
,
называетсяполярным
углом. Точка
![]() с полярными координатами обозначается:
с полярными координатами обозначается:![]() .
Пределы изменения полярных координат:
.
Пределы изменения полярных координат:![]() ,
,![]() .
Однако в некоторых случаях приходится
рассматривать углы больше
.
Однако в некоторых случаях приходится
рассматривать углы больше![]() ,
а также отрицательные углы, отсчитываемые
от полярной оси по часовой стрелке.
,
а также отрицательные углы, отсчитываемые
от полярной оси по часовой стрелке.
Типовой
пример.
Построить точку
![]() .
.
► 1. Проведем из
полюса луч под углом
1. Проведем из
полюса луч под углом
![]() к полярной оси.
к полярной оси.
2.
На этом луче отложим 4 единичных отрезка.
Получим точку
![]() .
◄
.
◄
3. Связь между
прямоугольными и полярными координатами.
С овместим
прямоугольную и полярную системы
координат так, чтобы полюс совпал с
началом координат, а полярная ось совпала
с положительным направлением оси
овместим
прямоугольную и полярную системы
координат так, чтобы полюс совпал с
началом координат, а полярная ось совпала
с положительным направлением оси![]() .
.
Пусть точка
![]() имеет прямоугольные координаты
имеет прямоугольные координаты![]() и полярные
и полярные![]() .
То
.
То
гда получим
|
|
а) формулы перехода от прямоугольных ко- ординат к полярным; | |
|
|
| |
|
|
б) формулы перехода от полярных координат к прямоугольным.
| |
Типовой
пример.
Уравнение окружности в прямоугольной
системе координат имеет вид
![]() .
Записать уравнение в полярной системе
координат.
.
Записать уравнение в полярной системе
координат.
► Перейдем
к полярным координатам
Перейдем
к полярным координатам
![]() ,
,![]() .
.
Следовательно,
![]()
![]()
![]()
![]()
![]()
![]()
![]() –это уравнение данной окружности в
полярной системе координат.
◄
–это уравнение данной окружности в
полярной системе координат.
◄
Типовой пример. Пусть задана кривая уравнением в полярных координатах
![]() .
.
Найти уравнение кривой в декартовых координатах.
►Имеем
 ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Итак,
![]() – уравнение кривой в декартовых
координатах (эллипс).◄
– уравнение кривой в декартовых
координатах (эллипс).◄
4. Преобразование прямоугольных координат. Переход от одной системы координат в какую-либо другую называется преобразованием системы координат. Рассмотрим два вида преобразований.
4.1.
Параллельный
перенос осей координат.
 Подпараллельным
переносом понимают
такое преобразование координат, при
котором меняется положение осей
координат, а направление и масштаб
остаются неизменными.
Подпараллельным
переносом понимают
такое преобразование координат, при
котором меняется положение осей
координат, а направление и масштаб
остаются неизменными.
Пусть
![]() –
координаты произвольной точки
–
координаты произвольной точки![]() в системе координат
в системе координат![]() .
Перенесем начало координат из точки
.
Перенесем начало координат из точки![]() в точку
в точку![]() .
Тогда в новой системе координат
.
Тогда в новой системе координат![]() координаты точки
координаты точки![]() будут
будут![]() :
:
|
|
- формулы, по которым можно найти новые координаты по известным старым и наоборот. |
4.2. Поворот осей координат. Под поворотом осей координат понимают такое преобразование координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остаются неизменными.
П овернем
систему координат
овернем
систему координат![]() на угол
на угол![]() .
Пусть
.
Пусть![]() – – произвольная точка плоскости.
– – произвольная точка плоскости.![]() –
координаты точки
–
координаты точки![]() в системе координат
в системе координат![]() ,
,![]() – координаты точки
– координаты точки![]() в системе координат
в системе координат![]() .
.
Введем
полярные координаты точки
![]() :
:![]() – координаты точки
– координаты точки![]() в системе координат
в системе координат![]() ,
,![]() –
координаты точки
–
координаты точки![]() в
системе координат
в
системе координат![]() .
.
По формулам перехода от прямоугольных координат к полярным имеем:
|
|
|
|
|
Но
![]() ,
,![]() .
.
|
Поэтому
|
- формулы, по которым можно найти новые координаты по известным старым. |
Или
![]() .
Здесь
.
Здесь![]() –матрица
поворота.
–матрица
поворота.
Найдем
значения
![]() и
и![]() с помощью полученных формул. Для этого
решим систему уравнений по формулам
Крамера:
с помощью полученных формул. Для этого
решим систему уравнений по формулам
Крамера:![]() ,
,
|
|
|
|
|
- формулы, по которым можно найти старые координаты по известным новым. |
Типовой
пример.
Определить координаты точки
![]() в новой системе координат
в новой системе координат![]() ,
если начало координат перенесли в точку
,
если начало координат перенесли в точку![]() ,
а затем оси координат повернули на угол
,
а затем оси координат повернули на угол![]() .
.
► Определим
координаты точки
Определим
координаты точки
![]() .
.
|
1)
в системе координат
|
|
|
2)
в системе координат
|
|
![]()
![]() .
Ответ:
.
Ответ:
![]() .
◄
.
◄


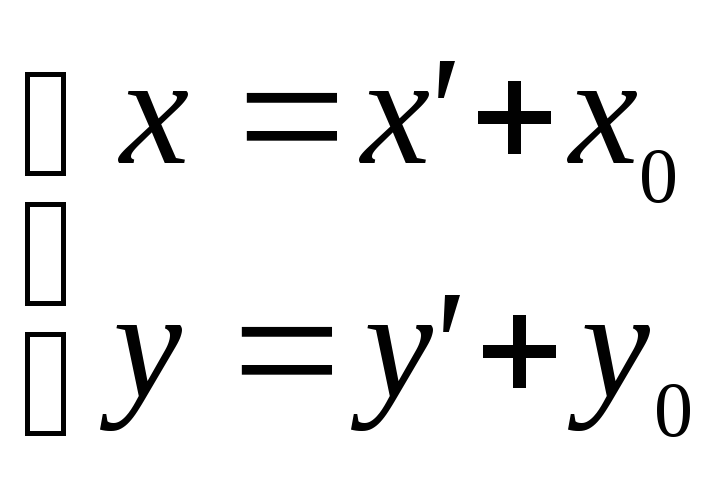 .
.