
- •Глава 4 векторная алгебра и аналитическая геометрия
- •§1. Векторная алгебра
- •§ 2. Системы координат на плоскости
- •§ 3. Прямая на плоскости
- •1. Общее уравнение прямой на плоскости
- •2. Частные случаи расположения прямой на плоскости.
- •3. Уравнение прямой, проходящей через данную точку: а) параллельной данной прямой; б) перпендикулярной данной прямой
- •4. Уравнение прямой, проходящей через две точки
- •5. Каноническое уравнение прямой
- •6. Параметрическое уравнение
- •7. Уравнение прямой с угловым коэффициентом
- •8. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой
- •Расстояние от точки до прямой на плоскости (второй способ)
- •0 1 2 3 4 5
- •§ 3. Плоскость
- •2. Расположение плоскости в пространстве. Уравнение плоскости в отрезках на осях
- •3. Уравнение плоскости, проходящей через три точки
- •5. Пучок плоскостей
- •6. Взаимное расположение плоскостей. Расстояние от точки до плоскости
- •§ 4. Прямая в пространстве
- •1. Общие уравнения прямой
- •3. Параметрические уравнения прямой
- •4. Уравнения прямой, проходящей через две точки
- •5. Взаимное расположение прямых в пространстве. Условие принадлежности двух прямых одной плоскости
- •§5. Прямая и плоскость в пространстве. Условие принадлежности прямой плоскости
- •§ 6. Линии второго порядка на плоскости
- •§7. Поверхности второго порядка
§7. Поверхности второго порядка
Поверхности второго порядка в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
По заданному уравнению поверхности будем определять ее внешний вид методом сечений, т.е. будем находить линии пересечения поверхности с координатными плоскостями или с плоскостями, параллельными координатным плоскостям.
1. Эллипсоид. Каноническое уравнение эллипсоида имеет вид
![]() .
.
1)
Находим линию пересечения эллипсоида
с плоскостью
![]()
![]() .
.
Решаем систему уравнений
|
|
- это уравнение эллипса с
полуосями
|
2 )
Находим линию пересечения эллипсоида
с плоскостью
)
Находим линию пересечения эллипсоида
с плоскостью![]()
![]() .
.
Решаем систему уравнений

![]()
![]() –
–
это уравнение эллипса с полуосями
![]() и
и
![]() .
.
3)
Находим линию пересечения эллипсоида
с плоскостью
![]()
![]() .
.
Решаем систему уравнений

![]()
![]()
– это
уравнение эллипса с полуосями
![]() и
и![]() .
.
Эллипсоид
– это
замкнутая овальная поверхность.
![]() ,
,![]() ,
,![]() – полуоси эллипсоида. Если
– полуоси эллипсоида. Если![]() ,
то эллипсоид превращается в сферу.
,
то эллипсоид превращается в сферу.
2. Однополостный гиперболоид. Каноническое уравнение имеет вид
![]()
Строим методом сечений.
1)
Находим линию пересечения с плоскостью
![]() .
.
Решаем
систему уравнений

![]()
![]()
-
это уравнение эллипса с полуосями
![]() и
и![]() .
.
2)
Находим линии пересечения с плоскостями,
параллельными плоскости
![]() :
:![]()
Решаем систему уравнений


![]()
![]()

-
это уравнение эллипса с полуосями
![]() и
и![]() .
.
3)
Находим линию пересечения с плоскостью
![]() .
.
Решаем
систему уравнений

![]()
![]() -
это уравнение гиперболы, где
-
это уравнение гиперболы, где![]() – действительная полуось, а
– действительная полуось, а![]() -
мнимая полуось.
-
мнимая полуось.
4)
Находим линию пересечения с плоскостью
![]() .
Решаем систему уравнений
.
Решаем систему уравнений

![]()
![]() -
это уравнение гиперболы.
-
это уравнение гиперболы.
![]() -
действительная полуось, а
-
действительная полуось, а
![]() – мнимая полуось.
– мнимая полуось.
Однополостный
гиперболоид
– это бесконечная труба, которая
бесконечно расширяется по мере удаления
от плоскости
![]() .
.![]() ,
,![]() ,
,![]() – это полуоси гиперболоида. Полуось
– это полуоси гиперболоида. Полуось![]() увидим, если построим основной
прямоугольник какой-либо из гипербол.
увидим, если построим основной
прямоугольник какой-либо из гипербол.
3. Двуполостный гиперболоид. Каноническое уравнение имеет вид
![]() .
.
1)
Находим линию пересечения с плоскостью
![]() .
.
Решаем систему уравнений:
|
|
– это уравнение мнимого эллипса. |
Следовательно,
с плоскостью
![]() нет общих точек.
нет общих точек.
2)
Находим линии пересечения с плоскостями,
параллельными плоскости
![]() :
:![]() .
.
а)
Решаем систему уравнений

![]()
![]() – это уравнение мнимого эллипса, так
как
– это уравнение мнимого эллипса, так
как![]() .
.
б) Решаем систему уравнений


![]()
![]() .
.
Получим
точки
![]() и
и![]() .
.
в) Решаем систему уравнений

![]()
![]() ;
;

– это
уравнение эллипса, с полуосями
![]() и
и![]() .
.
2)
Находим линию пересечения с плоскостью
![]() .
.
Решаем
систему уравнений

![]()
![]() .
.
Это
уравнение гиперболы, где
![]() -действительная полуось, а
-действительная полуось, а![]() -
мнимая полуось.
-
мнимая полуось.
3)
Находим линию пересечения с плоскостью
![]() .
Решаем систему уравнений
.
Решаем систему уравнений

![]()
![]() -
это уравнение гиперболы,
-
это уравнение гиперболы,
где
![]() -
действительная полуось, а
-
действительная полуось, а![]() – мнимая полуось.
– мнимая полуось.
Двуполостный
гиперболоид
– это две чаши с вершинами в точках
![]() и
и![]() ,
которые бесконечно расширяются по мере
удаления от плоскости
,
которые бесконечно расширяются по мере
удаления от плоскости![]() .
.![]() ,
,![]() и
и![]() -
полуоси гиперболы. Полуоси
-
полуоси гиперболы. Полуоси![]() и
и![]() увидим, если построим основные
прямоугольники обеих гипербол.
увидим, если построим основные
прямоугольники обеих гипербол.
4. Эллиптический параболоид. Каноническое уравнение имеет вид
![]() ,
,
где
![]() и
и![]() это параметры параболоида,
это параметры параболоида,![]() ;
;![]() ,
,
Строим методом сечений.
1)
Находим линию пересечения с плоскостью
![]() .
Решаем систему уравнений
.
Решаем систему уравнений

![]()
![]() –это уравнение
точки
–это уравнение
точки
![]() .
.
2 )
Находим линии пересечения с плоскостями,
параллельными
)
Находим линии пересечения с плоскостями,
параллельными
плоскости
![]() .
Решаем систему уравнений:
.
Решаем систему уравнений:

![]()
![]()
![]() –это уравнение
эллипса с полуосями
–это уравнение
эллипса с полуосями
![]() и
и![]() .
При
.
При![]() получим уравнение мнимого эллипса.
получим уравнение мнимого эллипса.
3)
Находим линию пересечения с плоскостью
![]() .
Решаем систему уравнений
.
Решаем систему уравнений

![]()
![]() –это уравнение
параболы симметричной относительно
оси
–это уравнение
параболы симметричной относительно
оси
![]() .
.
4)
Аналогично найдем линию пересечения с
плоскостью
![]() .
Это будет парабола
.
Это будет парабола![]() симметричная относительно оси
симметричная относительно оси![]() .
Если
.
Если![]() ,
то получаемпараболоид
вращения.
,
то получаемпараболоид
вращения.
5. Гиперболический параболоид. Каноническое уравнение имеет вид
![]() ,
,
где
![]() и
и![]() – это параметры параболоида,
– это параметры параболоида,![]() ;
;![]() ,
,
Строим
методом сечений. 1) Находим линию
пересечения с плоскостью
![]() .
Решаем систему уравнений
.
Решаем систему уравнений


![]()
![]() –это уравнение
параболы, симметричной относительно
оси
–это уравнение
параболы, симметричной относительно
оси
![]() .
.
2)Находим
линию пересечения с плоскостью
![]() .
Решаем систему уравнений
.
Решаем систему уравнений

![]()
![]() –это уравнение
параболы, симметричной относительно
оси
–это уравнение
параболы, симметричной относительно
оси
![]() .
.
3) Находим линии
пересечения с плоскостями, параллельными
плоскости
![]() .
.
а) Решаем систему уравнений

![]()
![]()
![]() –это уравнение
гиперболы, у которой
–это уравнение
гиперболы, у которой
![]() -
действительная полуось, а
-
действительная полуось, а![]() -
мнимая полуось.
-
мнимая полуось.
б) Решаем систему уравнений

![]()
![]()
![]() ( знак левой части
изменился, так как
( знак левой части
изменился, так как
![]() по условию) – это уравнение гиперболы,
у которой
по условию) – это уравнение гиперболы,
у которой![]() – действительная полуось, а
– действительная полуось, а![]() – мнимая полуось.
– мнимая полуось.
4)
Находим линию пересечения с плоскостью
![]() .
.
Решаем систему уравнений

![]()
![]() –это уравнение
двух прямых, проходящих через точку
–это уравнение
двух прямых, проходящих через точку
![]() .
.
Гиперболический параболоид – это поверхность, имеющая вид седла.
6. Конус второго порядка. Каноническое уравнение имеет вид
![]()
Строим методом сечений.
1)
Находим линию пересечения с плоскостью
![]()
![]() .
Решаем систему уравнений
.
Решаем систему уравнений


![]()
![]() –это уравнение
точки
–это уравнение
точки
![]() .
.
2)
Находим линии пересечения с плоскостями
параллельными
![]()
![]() .
Решаем систему уравнений
.
Решаем систему уравнений

![]()
![]()

![]()
 –это уравнение
эллипса с полуосями
–это уравнение
эллипса с полуосями
![]() и
и![]() .
.
3)
Находим линию пересечения с плоскостью
![]()
![]() .
Решаем систему уравнений
.
Решаем систему уравнений

![]()
![]() –это уравнение
двух прямых, проходящих через начало
координат.
–это уравнение
двух прямых, проходящих через начало
координат.
4)
Находим линию пересечения с плоскостью
![]()
![]() .
Решаем систему уравнений
.
Решаем систему уравнений


![]()
![]() –это уравнение
двух прямых, проходящих через начало
координат.
–это уравнение
двух прямых, проходящих через начало
координат.
7. Цилиндрические поверхности. Задаются уравнениями:
![]() ;
образующая параллельна оси
;
образующая параллельна оси
![]() ;
;
![]() ;
образующая параллельна оси
;
образующая параллельна оси
![]() ;
;
![]()
 ;
образующая параллельна оси
;
образующая параллельна оси
![]() ;
;
1. Эллиптический цилиндр
![]()
направляющая – эллипс,
образующая
параллельна оси
![]()
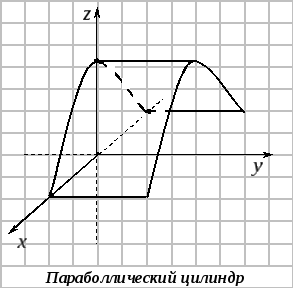
2. Параболический цилиндр
![]()
н аправляющая
– парабола,
аправляющая
– парабола,
образующая
параллельна оси
![]()
3. Гиперболический цилиндр
![]()
направляющая
– гипербола, образующая параллельна
оси
![]() .
.
Типовой пр имер.
Построить поверхность заданную
имер.
Построить поверхность заданную
![]() .
.
►Из
уравнения следует, что
![]() .
Возведем обе части уравнения в квадрат
.
Возведем обе части уравнения в квадрат![]()
![]()
![]()
![]() полусфера,
полусфера,![]() ,
с центром в точке
,
с центром в точке![]() .◄
.◄
Типовой пример. Построить тело, ограниченное поверхностями

 .
.
►Определим вид поверхностей.
![]() –параболический
цилиндр ;
–параболический
цилиндр ;
![]() –плоскость;
–плоскость;
![]() –координатные
плоскости. ◄
–координатные
плоскости. ◄


