2. Вычисление длин кривых

2.1. Определение спрямляемой кривой и длины кривой

Пусть на плоскости задана кривая . Разобьём эту кривую точкаминачастей и впишем в кривую ломаную, соединяющую эти точки. Длинаэтой ломанной равна сумме длин прямолинейных звеньев, соединяющих точки разбиения:. Устремим теперь количествоточек разбиения к бесконечности так, чтобы максимальная длина звенастремилась к нулю. Если при этом существует конечный предел последовательности длин ломаных, не зависящий от способа разбиения кривой, то кривая называется спрямляемой, а значение этого предела называется длиной кривой.

2.2. Длина кривой в декартовых координатах

Пусть теперь кривая _– график функции , имеющей непрерывную производную,. Тогда длина кривой, заданной декартовым уравнением,, определяется формулой.

Типовой пример

Найти длину отрезка параболы от точкидо точки.

►Здесь , поэтому

◄.

2.3. Кривая задана параметрически . Заменим впеременнуюна переменную. Так как, то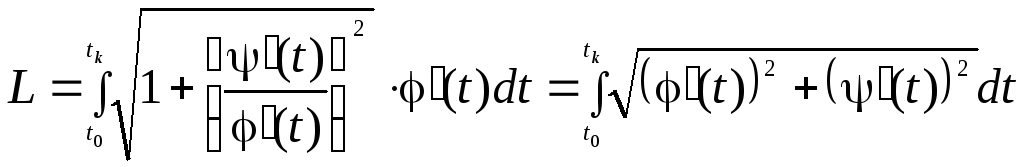. Итак, длина кривой, заданной параметрически, определяется формулой.

Типовой пример

Вычислить длину дуги кривой, заданной параметрическими уравнениями .

►Используем формулу . Вычислим,.

Тогда .◄

2.4. Кривая задана в полярных координатах

Случай, когда кривая задаётся уравнением ,, легко сводится к предыдущему. Так как, то, рассматривая полярный уголкак параметр, получим,

поэтому .

Типовой пример

Найти длину кардиоиды .

►Имеем 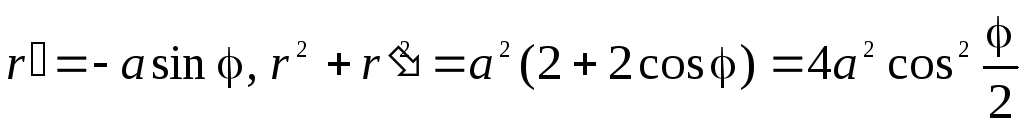, поэтому. Ответ явно бессмысленен. Где ошибка? Ошибка в том, что упущен знак модуля при извлечении корня из. Правильное решение:

Однако, как и в предыдущих случаях, проще воспользоваться симметрией фигуры, найти длину верхней ветви и удвоить её: ◄

3. Объёмы тел вращения

3.1. Вычисление объёма тела по площадям поперечных сечений Пусть тело расположено в пространстве между плоскостямии, и дляизвестна площадь его поперечного сечения. Объём этого тела.

3.2. Объём тела, получающегося при вращении кривой вокруг координатной оси

Если объём получается в результате вращения кривой,, вокруг оси, то, очевидно,, поэтому.

Типовой пример

Вычислить объем тела, полученного вращением кривых ивокруг оси.

►Выполним рисунок

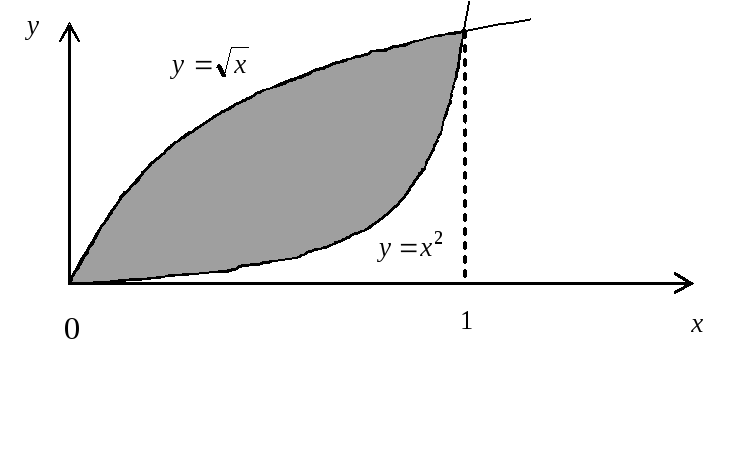
Находим точку пересечения кривых: ; ; . Объем искомого тела получится вычитанием из объема тела, полученного вращением кривой , объема тела, полученного вращением кривой:

ед. куб.  ед. куб. ◄

3.3. Объём тела, получающийся при вращении сектора, ограниченного кривой и двумя полярными радиусамии, вокруг полярной осинаходится по формуле .

Типовой пример

Найти объём тора, полученного вращением окружности вокруг полярной оси.

►

.◄

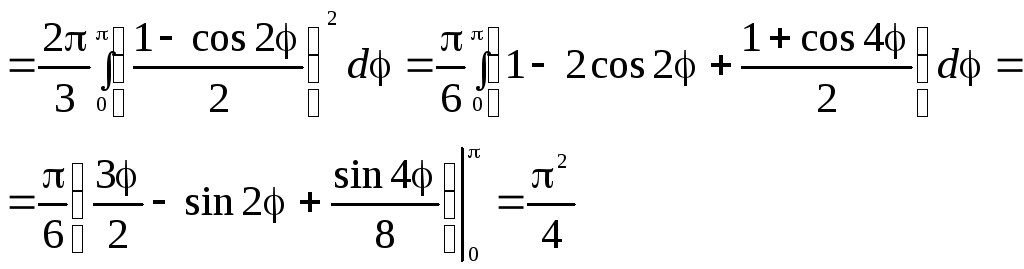4. Площадь поверхности вращения

Площадь поверхности вращения, образующейся при вращении вокруг оси дифференцируемой кривой, определяется по формулам (в зависимости от способа задания кривой)

(- длина окружности кольца,- его ширина).

Типовой пример

Найти площадь тора, образующегося при вращении окружности вокруг оси.

►Имеем .◄

§4. Определенный интеграл в экономике

1. Экономический смысл определенного интеграла

Пусть функция описывает изменение производительности некоторого производства с течением времени. Найдем объем продукции, произведенной за промежуток времени. Если производительность не изменяется с течением времени (– постоянная функция), то объем продукции, произведенной за некоторый промежуток времени, задается формулой. В общем случае справедливо равенство, где, которое оказывается тем более точным, чем меньше. Разобьем отрезокна промежутки времени точками:. Для величины объема продукции, произведенной за промежуток времени, имеем, где,,.

Тогда При стремлении к нулю каждое из использованных приближенных равенств становится все более точным, поэтому .

Используя определение определенного интеграла, окончательно получаем: , т.е. если – производительность труда в момент, то есть объем выпускаемой продукции за промежуток .

Величина и объем продукции, произведенной за промежуток , численно равны площади под графиком функции, описывающей изменение производительности труда с течением времени, на промежутке.

Пример

Известно, что численность населения определяется формулой , где - число жителей в начальный момент времени. Известно также, что потребление населением в единицу времени некоторого продукта пропорционально числу жителей. Пусть коэффициент пропорциональности равен , тогда функция потреблениябудет иметь вид:. Найти объем продукта, необходимого для потребления на промежуток времени.

►В малый промежуток времени количество жителей будем считать постоянным, следовательно, за этот элементарный промежуток времени потребляется количество продукта. Интегрируя это равенство, получим количествопродукта, необходимое для населения на весь промежуток времени отдо .◄